Hans Walser, [20190210]

Rationaler Kosinus

1 Winkel und Vielfache

Wir arbeiten mit einem Winkel mit einem rationalen Kosinus-Wert:

(1)

Dann hat auch jedes ganzzahlige Vielfache dieses Winkels einen rationalen Kosinus-Wert:

(2)

2 Beweis

Für den Beweis benötigen wir die Formeln von de Moivre, die wir kurz herleiten. Aus der Formel von Euler

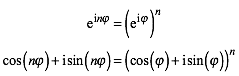(3)

folgt durch Expandieren:

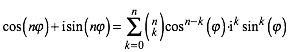(4)

Trennung in Real- und Imaginärteil liefert die Formeln von de Moivre:

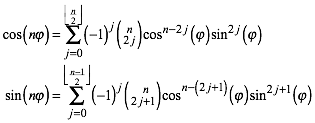(5)

Weiter ist

(6)

rational. Die Sinuswerte selber sind in der Regel nicht rational (ausgenommen im Kontext mit pythagoreischen Dreiecken).

In der Formel (5) für kommen die Sinuswerte nur mit geraden Exponenten vor. Daher ist rational.

Wir haben jetzt allerdings nur bewiesen, dass rational ist (Existenzbeweis), können diese rationale Zahl aber nicht mit Zähler und Nenner darstellen. Dazu dienen die weiteren Überlegungen.

3 Bezeichnungen

Wir verwenden folgende Bezeichnungen:

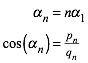(7)

4 Beispiel

Es sei und (Abb. 1).

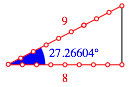
Abb. 1: Beispiel

Damit ist:

(8)

In der Tabelle 1 ist in der letzten Spalte der Kosinus der Vielfachen des Winkels angegeben. In der zweiten und dritten Spalte sind ganze Zahlen angegeben, deren Quotient (vierte Spalte) mit dem Kosinuswert des Vielfachen des Winkels (numerisch) übereinstimmt. Abweichungen ergeben sich erst in den hinteren Dezimalstellen und dürften rundungsbedingt sein.

n
1	8	9	0.8888888889	0.8888888889
2	47	81	0.5802469136	0.5802469137
3	104	729	0.1426611797	0.1426611797
4	–2143	6561	–0.3266270386	–0.3266270380
5	–42712	59049	–0.7233314705	–0.7233314703
6	–509809	531441	–0.9592955756	–0.9592955756
7	–4697272	4782969	–0.9820828862	–0.9820828863
8	–33861823	43046721	–0.7866295554	–0.7866295555
9	–161310136	387420489	–0.4163696567	–0.4163696575
10	161845487	3486784401	0.0464168324	0.0464168318
11	15655648808	31381059609	0.4988884698	0.4988884695
12	237380896481	282429536481	0.8404960028	0.8404960023

Tab. 1: Beispiel

In der dritten Spalte ist offensichtlich:

(9)

Die Zahlen in der zweiten Spalte genügen der Rekursion:

(10)

Dies ist nicht offensichtlich und muss begründet werden.

5 Konstruktiver Beweis

Wir gehen aus von der Situation und den Bezeichnungen der Formel (1) (Abb. 2). Gegeben sind also und .

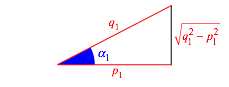
Abb. 2: Allgemeine Startsituation

Es ist:

(11)

Weiter sei:

(12)

Die Werte seien definiert durch die Startwerte und das gegebene sowie durch die Rekursion:

(13)

Wir wollen zeigen:

(14)

Dazu erarbeiten wir die verallgemeinerte Formel von Binet für die durch (13) mit den zugehörigen Startwerten gegebene Folge.

Diese Formel von Binet hat die allgemeine Form:

(15)

Dabei sind und die Lösungen der sich aus (13) ergebenden quadratischen Gleichung

(16)

während sich die Koeffizienten r und s aus den Startwerten ergeben. Die Gleichung (16) hat die beiden Lösungen:

(17)

Wegen ist der Radikand in (17) negativ und wir haben die beiden konjugiert komplexen Lösungen:

(18)

Wenn wir in (15) setzen, können wir mit (18) verifizieren, dass die Startwerte der Folge erfüllt sind.

Wegen (11) können wir die Lösungen (18) der quadratischen Gleichung (16) schreiben in der Form:

(19)

Somit erhalten wir aus (12), (15) und (19) für die Formel von Binet:

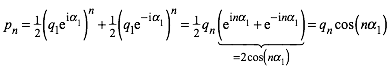(20)

Daraus ergibt sich (14). Dies war zu zeigen.

6 Gleichschenklige Dreiecke

Wir können das Dreieck der Abbildung 1 zu einem gleichschenkligen Dreieck mit dem rationalen Seitenverhältnis 9:9:16 ergänzen (Abb. 3).

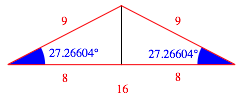
Abb. 3: Gleichschenkliges Dreieck mit rationalem Seitenverhältnis

Wenn wir nun die Basiswinkel verdoppeln, erhalten wir ein gleichschenkliges Dreieck mit dem ebenfalls rationalen Seitenverhältnis 81:81:94 (Tab. 1, Abb. 4).

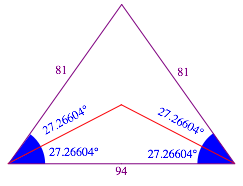
Abb. 4: Doppelte Basiswinkel

Wie sieht die Situation bei einer Verdreifachung, Vervierfachung, ... der Basiswinkel aus?

Weblinks

Hans Walser: Rationale Seitenverhältnisse

www.walser-h-m.ch/hans/Miniaturen/R/Rationale_Seitenverhaeltnisse/Rationale_Seitenverhaeltnisse.htm