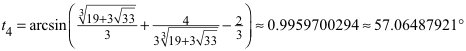1 Worum es geht

Kinematische Spielerei im Halbkreis. Es erscheinen Winkel im Kontext von √2, √3 und dem Goldenen Schnitt.

2 Kinematik

Die beiden grünen Strecken sind orthogonal.

Abb. 1: Kinematik im Halbkreis

Wir untersuchen drei spezielle Stationen des Vorgangs.

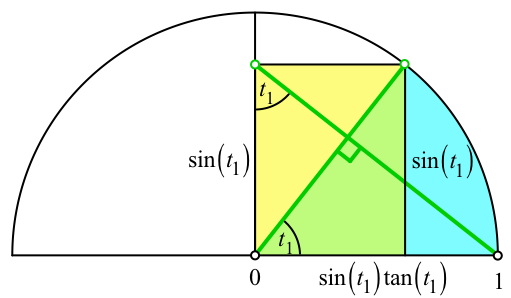
Abb. 2: Erster Anschlag

Für den ersten Anschlag (Abb. 2) erhalten wir die Bedingung:

sin(t₁) tan(t₁) = 1

Dies kann umgeformt werden zu:

sin(t₁) sin(t₁)/√(1 – sin²(t₁))= 1

Daraus ergibt sich die biquadratische Gleichung für sin(t₁):

sin⁴(t₁) + sin²(t₁) – 1 = 0

Die für uns relevante Lösung dieser biquadratischen Gleichung für sin(t₁) ist (dabei ist Φ der Goldene Schnitt):

sin(t₁) = √(1/ Φ)

Somit ist:

t₁ = arcsin(√(1/ Φ)) ≈ 0.904556894302381 ≈ 51.827292372987753°

(Bemerkung: dies soll näherungsweise der Neigungswinkel der Seitenflächen der Cheops-Pyramide sein.)

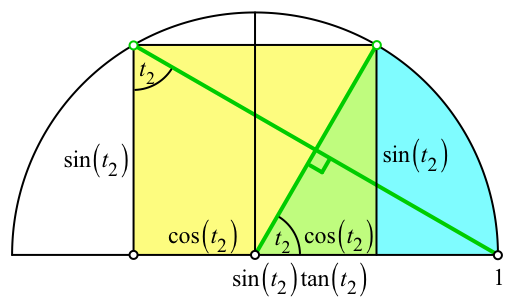
Abb. 3: Zweiter Anschlag

Für den zweiten Anschlag (Abb. 3) erhalten wir die Bedingung:

sin(t₂) tan(t₂) = 1 + cos(t₂)

Dies kann umgeformt werden:

sin²(t₂) = cos(t₂) + cos²(t₂)

2 cos²(t₂) + cos(t₂) – 1 = 0

Die für uns relevante Lösung ist cos(t₂) = ½. Damit ist:

t₂ = arccos(½) = π/3 = 60°.

Die Figur lässt sich in ein regelmäßiges Sechseck einpassen (Abb. 4). Das Längenverhältnis der beiden grünen Strecken ist √3:1.

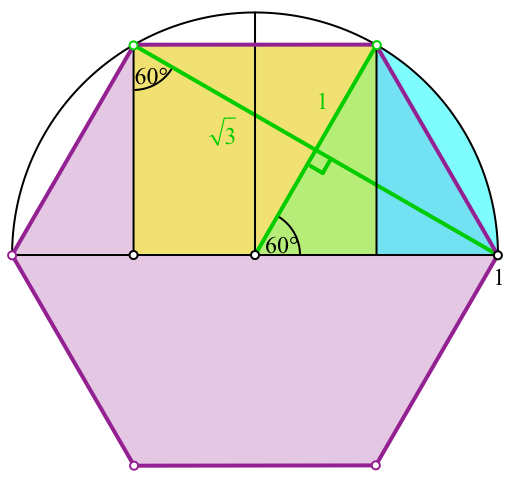
Abb. 4: Regelmäßiges Sechseck

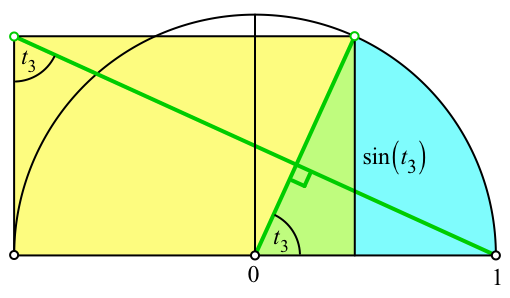
Abb. 5: Dritter Anschlag

Für den dritten Anschlag (Abb. 5) erhalten wir die Bedingung:

sin(t₃) tan(t₃) = 2

Dies kann umgeformt werden:

cos²(t₃) + 2cos(t₃) – 1 = 0

Die für uns relevante Lösung ist cos(t₃) = √2 – 1. Damit ist:

t₃ = arccos(√2 – 1) ≈ 1.14371774040242 ≈ 65.530199479297808°

Die Figur lässt sich in ein Rechteck im DIN-Format (Seitenverhältnis = √2:1) einpassen (Abb. 6).

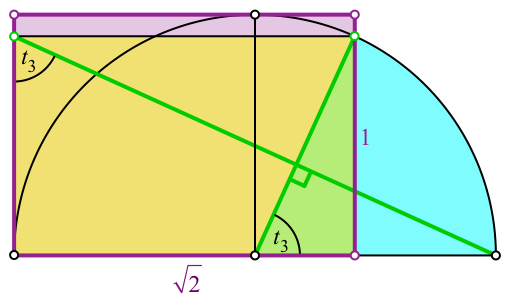
Abb. 6: DIN-Format

Für welchen Parameterwert t₄ergibt sich ein Quadrat (Abb. 7)?

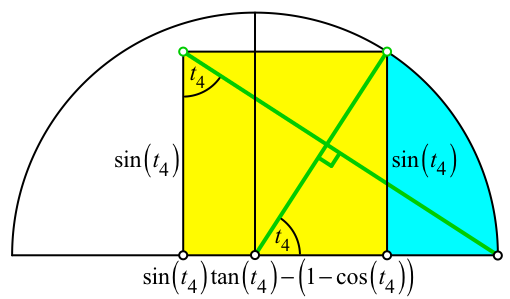
Abb. 7: Quadrat

Für ein Quadrat (Abb. 7) erhalten wir die Bedingung:

sin(t₄) = sin(t₄) tan(t₄) – (1 – cos(t₄))

Dies führt auf:

sin⁴(t₄) +2sin²(t₄) – 2sin(t₄) = 0

Die für uns relevante Lösung ist: