1 Worum geht es?

Ein Rhombenproblem. Zerlegungen. Rhombenparkett

2 Problemstellung

Ein gegebenes Rechtreck lasse sich in der unteren Hälfte eines Rhombus im Querformat und in der oberen Hälfte im Hochformat einpassen (Abb. 1a).

Gesucht ist das Diagonalenverhältnis des Rhombus.

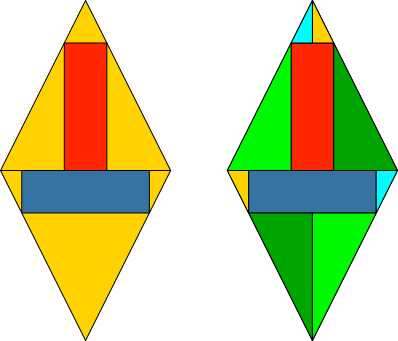
Abb. 1: Zwei gleiche Rechtecke

Die Abbildung 1b zeigt eine gemeinsame Zerlegung der unteren und oberen Resthälfte des Rhombus.

3 Bearbeitung

Das Rechteck habe im Querformat die Länge a und die Breite b (Abb. 2a).

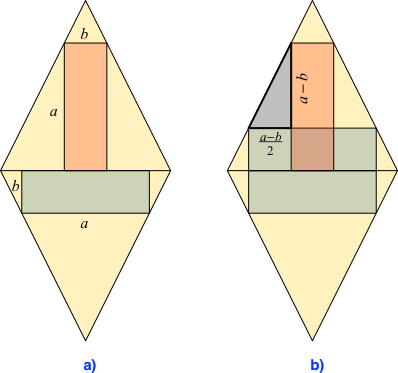
Abb. 2: Maße und Bearbeitung

Wir spiegeln nun das Rechteck von der unteren Hälfte in die obere Hälfte (Abb. 2b). Das grau markierte rechtwinklige Dreieck hat die horizontale Kathete (a – b)/2 und die vertikale Kathete a – b. Daher hat die Hypotenuse die Steigung 2. Dies ist auch das gesuchte Diagonalenverhältnis des Rhombus.

Das Diagonalenverhältnis des Rhombus ist also unabhängig von den Ausmaßen a und b des Rechteckes. Den Autor hat dies etwas verblüfft.

4 Animationen

Die Abbildungen 3 und 4 illustrieren den Sachverhalt.

Abb. 3: Veränderung des Rechteckes

Abb. 4: Gemeinsame Zerlegung

5 Parkette

Im Rhombenparkett haben die blauen und roten Rechtecke benachbarter Rhomben gemeinsame Eckpunkte (Abb. 5, 6 und 7).

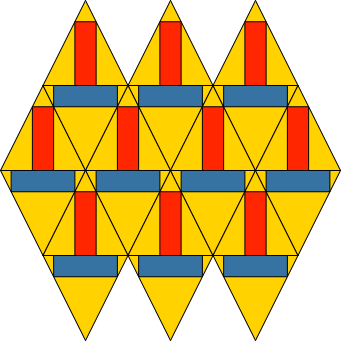
Abb. 5: Rhombenparkett

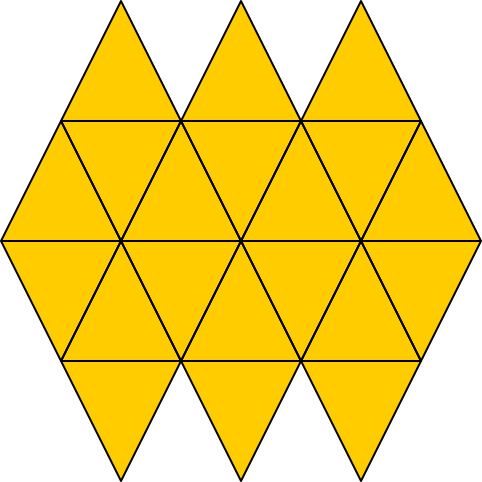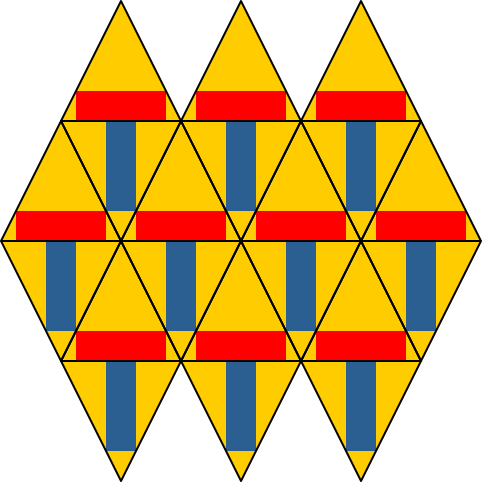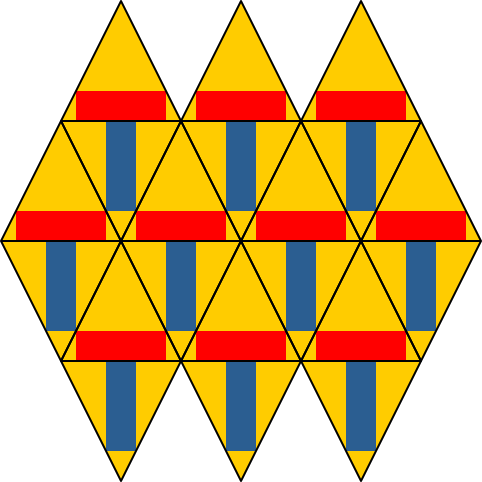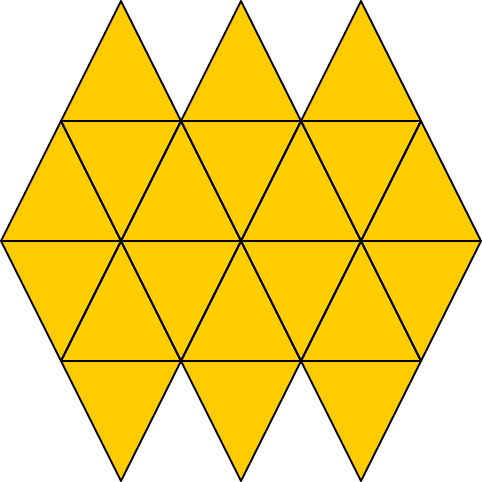
Abb. 6: Rhombenparkett

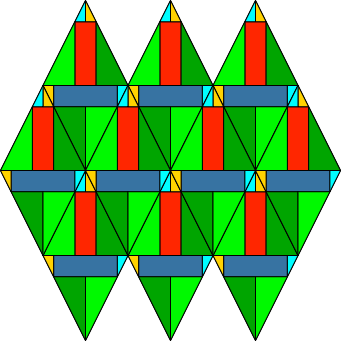
Abb. 7: Parkett mit Zerlegung

6 Zusatz: Goldener Schnitt

Wir passen in die obere Hälfte unseres Rhombus einen zweiten Rhombus ein gemäß Abbildung 8. Das Diagonalenverhältnis dieses Rhombus ist der Goldene Schnitt.

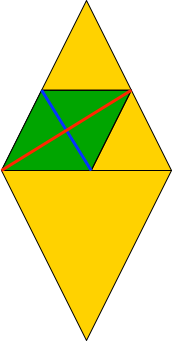
Abb. 8: Goldener Schnitt

Weblink

Hans Walser: Quadrate im Rhombus

http://www.walser-h-m.ch/hans/Miniaturen/Q/Quadrate_im_Rhombus/Quadrate_im_Rhombus.html