Hans Walser, [20090214b]

Eine Rechtecksbedingung

1 Worum es geht

In einem Parallelogramm wählen wir einen beliebigen Punkt und verbinden ihn durch die Strecken p, q, r, s mit den Eckpunkten.

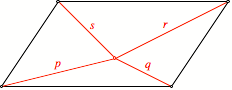
Ausgangsfigur

Das Parallelogramm ist genau dann ein Rechteck, wenn

2 Vektorieller Beweis

Wir arbeiten mit Vektoren gemäß Figur.

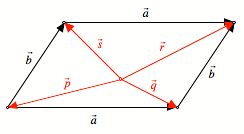
Vektoren

Nun drücken wird die Vektoren durch die Vektoren aus und bilden die Quadrate:

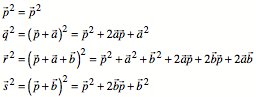
Für die alternierende Quadratsumme erhalten wir:

Daraus folgt die Behauptung.

3 Pyramide

Der vektorielle Beweis ist nicht an die Ebene gebunden. Wenn wir den Punkt oberhalb des Grundparallelogramms wählen, ergibt sich eine Pyramide.

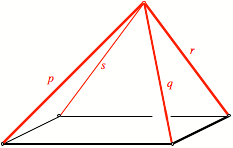
Pyramide

Eine Pyramide auf einer Parallelogrammbasis hat also genau dann eine rechteckige Basis, wenn die alternierende Quadratsumme der Schrägkanten verschwindet.