Hans Walser, [20200610]
Rechtecksfolgen
1 Worum geht es?
Eine Eigenschaft des DIN-Rechteckes lŠsst sich auf zwei Arten verallgemeinern.
2 Das DIN-Rechteck
Das
DIN-Rechteck hat das SeitenverhŠltnis 
. †ber das DIN-Format siehe Walser (2013). Wird von
einem DIN-Rechteck ein Quadrat abgeschnitten, bleibt ein Rechteck Ÿbrig (das
sogenannte ãsilberneÒ Rechteck), dessen Diagonalen sich unter 45¡ schneiden
(Abb. 1).
Abb. 1: DIN-Rechteck
Die Frage ist, welche Kriterien fŸr ein weiteres Rechteck gelten sollen:
a) Fortlaufendes Halbieren des Diagonalen-Schnittwinkels. Dies fŸhrt zu einer geometrischen Folge.
b) Abnahme des Diagonalen-Schnittwinkels im Sinne einer harmonischen Folge, also Halbieren, Dritteln, Vierteln, FŸnfteln und so weiter.
3 Fortlaufendes Halbieren des Diagonalen-Schnittwinkels
3.1 Die Figuren
Die Abbildungen 2 und 3 zeigen die beiden nŠchsten Schritte.
Abb. 2: NŠchster Schritt
Abb. 3: †bernŠchster Schritt
Die
Diagonalenschnittwinkel sind der Reihe nach: 
3.2 Konvergenz
Es ist anzunehmen, dass die Rechtecksreihe konvergiert. Geometrische Reihen haben das ja an sich. NatŸrlich ist zu beachten, dass nur die Schnittwinkel der Diagonalen eine abnehmende geometrische Folge bilden.
TatsŠchlich konvergiert auch die Rechtecksreihe (Abb. 4). Bei einer SeitenlŠnge 1 des Startquadrates ergibt sich mit CAS fŸr die Hšhe der Rechtecksreihe ein Grenzwert von etwa 1.809837202. Der ganze Rest macht zusammen weniger aus als das Startquadrat.
Abb. 4: Rechtecksreihe
Die Welt will betrogen sein. In der Abbildung 4 sind tatsŠchlich nur 20 Rechtecke (inklusive Startquadrat) gezeichnet worden. Das gibt eine Gesamthšhe von 1.809835702. Stimmt also nur auf 5 Dezimalstellen.
Nun zum Beweis der Konvergenz. Aus der Abbildung 4c lesen wir fŸr die Gesamthšhe ab:
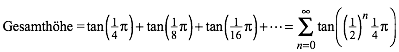(1)
Wir
arbeiten mit dem Majorantenkriterium. FŸr 
ist 
(Abb. 5).
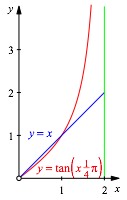
Abb. 5: Majorante
Somit folgt aus (1):
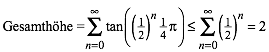(2)
Vergleiche dazu [1].
3.3 Schšne Figuren
Die roten und blauen Dreiecke der Abbildung 4b kšnnen gemŠ§ Abbildung 6 angeordnet werden.
Abb. 6: Schšne Figur
Die roten und blauen Dreiecke der Abbildung 4c kšnnen gemŠ§ Abbildung 7 angeordnet werden (vgl. [1]).
Abb. 7: Noch eine schšne Figur
Die oberen Ecken der Dreiecke liegen exakt auf der Oberkante des unterlegten gelben Einheitsquadrates. Damit kann die Konvergenz von (1) illustriert werden. Das Rechteck der Abbildung 4c hat die Breite 1. Damit hat seine Gesamthšhe die gleiche Ma§zahl wie die FlŠche. Die roten und blauen Dreiecke machen die halbe FlŠche aus. Diese ist nach Abbildung 7 kleiner als 1. Somit ist die Gesamthšhe kleiner als 2.
4 Harmonische Abnahme
Die Abbildungen 8 und 9 zeigen die beiden nŠchsten Schritte.
Abb. 8: NŠchster Schritt
Abb. 9: †bernŠchster Schritt
Die
Diagonalenschnittwinkel sind der Reihe nach: 
Die Abbildung 10 zeigt die Situation nach 20 Schritten.
Abb. 10: Nach 20 Schritten
Die Sache
divergiert (war zu erwarten). FŸr den Beweis der Divergenz arbeiten wir mit dem
Minorantenkriterium. ZunŠchst ist fŸr 
: 
Die Gesamthšhe wŠre:
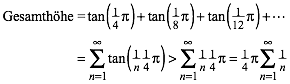(3)
Nun ist in (3) die letzte Reihe aber die divergente harmonische Reihe.
Literatur
Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.
Websites
[1] Hans Walser: Beweis ohne Worte
www.walser-h-m.ch/hans/Miniaturen/B/Beweis_ohne_Worte3/Beweis_ohne_Worte3.htm