Hans Walser, [20111220a]

Rechtecksunterteilung

Anregung: F. E., V.

Ein Rechteck wird in dazu Šhnliche Rechtecke unterteilt. Neben dem Quadrat gibt das DIN-Rechteck einige schšne Beispiele her. Auch die pythagoreischen Zahlentripel spiele eine exemplarische Rolle.

1        Beispiele

1.1      Sonderfall Quadrat

Wir halbieren die Seiten eines Quadrates und verbinden gemŠ§ Abbildung 1.

 

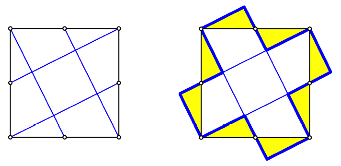
Abb. 1: Unterteilung eines Quadrates

 

Dann entsteht in der Mitte ein Quadrat, dessen FlŠche ein FŸnftel der FlŠche des Ausgangsquadrates ist. Dies kann mit einem Puzzle-Beweis eingesehen werden.

1.2      Rechteck im DIN-Format

Bei einem Rechteck im DIN-Format unterteilen wir die Seiten je in drei Teile. Dann verbinden wir gemŠ§ Abbildung 2.

 

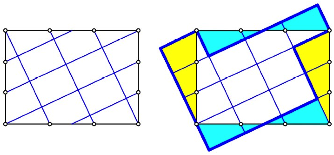
Abb. 2: Unterteilung eines DIN-Rechteckes

 

Es entstehen Rechtecke, welche zum Ausgangsrechteck Šhnlich sind (Beweis?). Der FlŠcheninhalt eines Teilrechteckes ist ein Elftel des FlŠcheninhaltes des Ausgangsrechteckes. Dies kann mit einem Puzzle-Beweis eingesehen werden.

1.3      Nochmals: Rechteck im DIN-Format

Bei einem Rechteck im DIN-Format unterteilen wir die LŠngsseite in vier und die Schmalseite in zwei Teile. Dann verbinden wir gemŠ§ Abbildung 3.

 

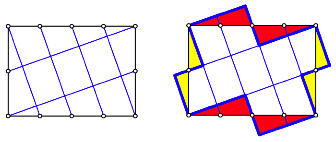
Abb. 3: Unterteilung eines DIN-Rechteckes

 

Es entstehen Rechtecke, welche zum Ausgangsrechteck Šhnlich sind (Beweis?). Der FlŠcheninhalt eines Teilrechteckes ist ein Neuntel des FlŠcheninhaltes des Ausgangsrechteckes. Auch dies kann mit einem Puzzle-Beweis eingesehen werden. Im Unterschied zum Beispiel der Abbildung 2 stehen die Teilrechtecke annŠhernd im Hochformat.

2        Allgemeine Situation

2.1      Unterteilung

Wir arbeiten in einem Rechteck im Querformat mit den Seiten a und b, . Die Seite a unterteilen wir in m gleiche Teile, die Seite b in n gleiche Teile. Weiter wŠhlen wir zwei Zahlen  und  gemŠ§ Abbildung 4. Die Abbildung 4 entspricht dem Fall , ,  und .

 

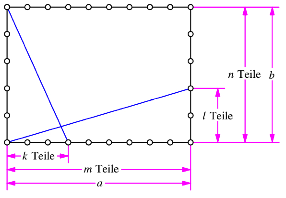
Abb. 4: Unterteilungen

 

Die beiden schrŠgen blauen Linien nehmen wir als Basis fŸr eine Parallelogrammrasterung (Abb. 5).

 

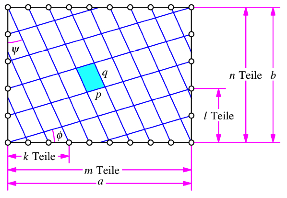
Abb. 5: Parallelogrammraster

 

2.2      Orthogonalisierung

Wir verlangen nun, dass die Parallelogramme Rechtecke sein sollen. Dazu mŸssen die beiden Parallelenscharen orthogonal sein. Diese OrthogonalitŠtsbedingung ergibt:

 

 

 

 

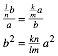
Also ist (OrthogonalitŠtsbedingung):

 

 

 

Zu gegebenem a ist also b bestimmt. FŸr das Beispiel Fall , ,  und  erhalten wir . Die Abbildung 6 zeigt das korrigierte Rechteck. (Als Folge der erforderlichen affinen Streckung in vertikaler Richtung erscheinen die ursprŸnglich kreisfšrmigen Punktsignaturen nun als stehende Ellipsen.)

 

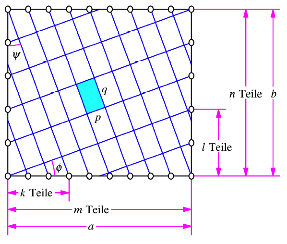
Abb. 6: Orthogonalisierte Version

 

Es ist dann  und weiter:

 

 

 

 

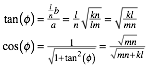
Ferner ist:

 

 

 

 

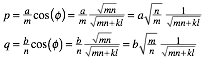
FŸr den FlŠcheninhalt eines Rasterrechteckes erhalten wir daraus:

 

 

Wir haben also flŠchenmŠ§ig  Rasterrechtecke im Ausgangsrechteck. 

2.3      €hnlichkeit

Weiter sollen die Rasterrechtecke Šhnlich zum Ausgangsrechteck sein. Dazu sind zwei FŠlle zu unterscheiden:

Erster Fall (ãQuerformatÒ):             

Zweiter Fall (ãHochformatÒ):          

2.3.1    Teilrechtecke Querformat

Wir erhalten die Bedingung:

 

 

 

Daraus ergibt sich die Querformatsbedingung:

 

 

Es ist dann , und wir haben flŠchenmŠ§ig  Rasterrechtecke im Ausgangsrechteck. 

2.3.2    Teilrechtecke Hochformat

Wir erhalten die Bedingung:

 

 

 

Also: . Wegen der OrthogonalitŠtsbedingung  ergibt sich:

 

 

 

Wir erhalten die Hochformatsbedingung:

 

Es ist , und wir haben flŠchenmŠ§ig  Rasterrechtecke im Ausgangsrechteck. 

2.4      †bersicht

 

Bedingung

Format Ausgangsrechteck

Anzahl Rasterrechtecke

Teilrechtecke
Querformat

Teilrechtecke
Hochformat

3        Weitere Beispiele

3.1      Raster parallel zu Rechtecksseiten

Die Rasterlinien sollen parallel zu den Seiten des Ausgangsrechteckes sein. In diesem Fall ist  und .

3.1.1    Teilrechtecke Querformat

Es ist zunŠchst  und . Die zweite Formel macht aber fŸr  und  keinen Sinn. Aus der ursprŸnglichen Form fŸr die OrthogonalitŠtsbedingung, also

 ,

 

 

 

erhalten wir in unserem Fall . Die Seiten des Ausgangsrechteckes sind unabhŠngig voneinander, wir kšnnen ein beliebiges Ausgangsrechteck unterteilen. Die Abbildung 7 zeigt die Situation fŸr . Wir erhalten  Rasterrechtecke.

 

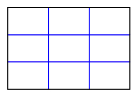
Abb. 7: Parallele Unterteilung im Querformat

 

3.1.2    Teilrechtecke Hochformat

Die Bedingung  ist ohnehin erfŸllt. FŸr das Ausgangsrechteck haben wir die Formatbedingung . Wir erhalten  Teilrechtecke.

Das bekannteste Beispiel ist der Fall  und , also das DIN-Format mit . Aus einem DIN A4 Papier ergeben sich durch Halbieren zwei DIN A5 Papiere (Abb. 8).

 

Abb. 8: Halbieren im DIN-Format

 

Als weiteres Beispiel den Fall  und , also  (Abb. 9). Das Ausgangsrechteck lŠsst sich in ein gleichseitiges Dreieck einpassen. Es ergeben sich 12 Teilrechtecke.

 

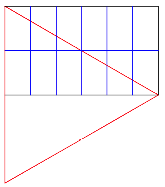
Abb. 9: Unterteilung im doppelten halben Dreieck

 

Die Abbildung 10 zeigt eine davon abgeleitete Unterteilung des gleichseitigen Dreieckes in zwšlf flŠchengleiche Teile.

 

Abb. 10: Unterteilung des Dreiecks

 

3.2      Spezielle Ausgangsrechtecke

3.2.1    Quadrat

Das Quadrat ist sowohl Querformat wie auch Hochformat. Wir haben daher die beiden Bedingungen  und . Viel Spielraum gibt es da nicht. Die Abbildung 11 zeigt die Situation fŸr den Fall  und . Wir erhalten  Teilquadrate. Diese 25 Teilquadrate lassen sich natŸrlich quadratisch anordnen, das Gesamtquadrat ist aber flŠchengleich und damit kongruent zum Ausgangsquadrat. Es geht aus diesem durch eine Drehung um den Winkel  hervor.

FŸr den Puzzle-Beweis mŸssen wir Teile umlegen (spiegeln).

 

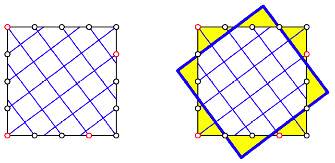
Abb. 11: Unterteilung des Quadrates

 

Das Beispiel ist allerdings etwas speziell, weil die Zahlen  und  zum pythagoreischen Zahlentripel 3, 4, 5 gehšren.

Die Abbildung 12 zeigt das analoge Beispiel fŸr Zahlen  und , welche zum pythagoreischen Zahlentripel 5, 12, 13 gehšren. Es  gibt  Teilquadrate, die wir eine einem  anordnen kšnnen.

 

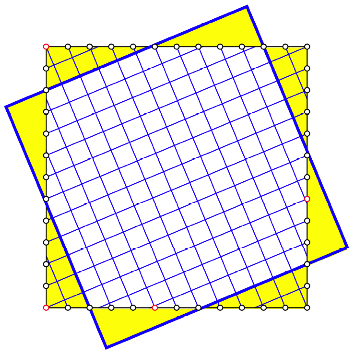
Abb. 12: Pythagoreisches Zahlentripel 5, 12, 13

 

Wir werden hier Opfer einer optischen TŠuschung, indem wir meinen, dass das Ausgangsquadrat (das ist dasjenige mit den Unterteilungspunkten) schief im Satzspiegel hŠngt. Dies ist aber nicht der Fall, wie man durch Nachmessen sich Ÿberzeugen kann.

Die Zahlen  und  gehšren nicht zu einem pythagoreischen Zahlentripel. Es gibt  Teilquadrate (Abb. 13), und die kšnnen wir nicht quadratisch anordnen. Es bleibt eins Ÿbrig.

 

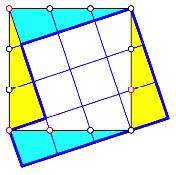
Abb. 13: Es bleibt eins Ÿbrig

 

3.2.2    DIN-Rechteck

Im DIN-Rechteck ist . Im Vergleich mit den Formatbedingungen fŸr Querformat, also , beziehungsweise Hochformat, also , sehen wir die Bedingungen  beziehungsweise .

Im Querformat-Fall ergeben sich  Teilrechtecke, im Hochformatfall  Teilrechtecke.

Als Beispiel (Abb. 14) den Querformat-Fall mit ,  und . Man beachte, dass . Es geht trotzdem.

 

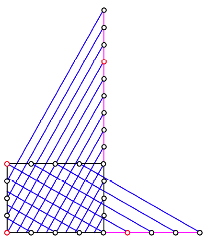
Abb. 14: Querformat?

 

Die Teilrechtecke scheinen eher im Hochformat zu stehen.

Wir mŸssen den Begriff ãQuerformatÒ prŠzisieren: Die Teilrechtecke stehen im Querformat, wenn ihre LŠngsseite die Richtung der von der linken unteren Ecke des Ausgangsrechteckes ausgehenden Rasterlinie hat.