Hans Walser, [20170819]
Rechtecksunterteilung
1 Worum geht es?
Wir unterteilen ein Rechteck mit ganzzahligen SeitenlŠngen m und n in mšglichst wenige Quadrate.
Die Abbildung 1 zeigt das Beispiel m = 93 und n = 36.

Abb. 1: Unterteilung in Quadrate
2 Der Algorithmus
Das Verfahren geht so:
Wir beginnen mit dem Rechteck der Breite 93 und der Hšhe 36. Davon schneiden wir Quadrate der SeitenlŠnge 36 ab. Das geht zwei Mal, da:
![]() (1)
(1)
Es bleibt ein Rechteck der Breite 21 und der Hšhe 36 źbrig. Davon schneiden wir Quadrate der SeitenlŠnge 21 ab. Das geht nur ein Mal, da:
![]() (2)
(2)
Es bleibt ein Rechteck der Breite 21 und der Hšhe 15 źbrig. Davon schneiden wir Quadrate der SeitenlŠnge 15 ab. Das geht ein Mal, da:
![]() (3)
(3)
Es bleibt ein Rechteck der Breite 6 und der Hšhe 15 źbrig. Davon schneiden wir Quadrate der SeitenlŠnge 6 ab. Das geht zwei Mal, da:
![]() (4)
(4)
Es bleibt ein Rechteck der Breite 6 und der Hšhe 3 źbrig. Davon schneiden wir Quadrate der SeitenlŠnge 3 ab. Das geht exakt zwei Mal, da:
![]() (5)
(5)
Wir sind fertig.
Die Gleichungen (1) bis (5) sehen zusammengefasst so aus:
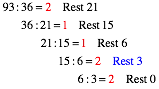 (6)
(6)
Das ist aber der Euklidische Algorithmus zur Bestimmung des grš§ten gemeinsamen Teilers. Dies ist der letzte von null verschiedene Rest (blau).
In unsrem
Beispiel ist ![]() .
.
Die Summe der rot markierten Zahlen ist die Gesamtzahl der benštigten Quadrate. In unserem Beispiel benštigen wir 8 Quadrate.
3 Tabellen
Die Tabelle 1 gibt die Anzahlen der benštigten Quadrate in AbhŠngigkeit von m und n. Vergleiche dazu das Zahlendreieck A113881:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
2 |
1 |
3 |
2 |
4 |
3 |
5 |
4 |
6 |
5 |
7 |
6 |
8 |
7 |
9 |
8 |
10 |
9 |
11 |
10 |
|
3 |
3 |
1 |
4 |
4 |
2 |
5 |
5 |
3 |
6 |
6 |
4 |
7 |
7 |
5 |
8 |
8 |
6 |
9 |
9 |
|
4 |
2 |
4 |
1 |
5 |
3 |
5 |
2 |
6 |
4 |
6 |
3 |
7 |
5 |
7 |
4 |
8 |
6 |
8 |
5 |
|
5 |
4 |
4 |
5 |
1 |
6 |
5 |
5 |
6 |
2 |
7 |
6 |
6 |
7 |
3 |
8 |
7 |
7 |
8 |
4 |
|
6 |
3 |
2 |
3 |
6 |
1 |
7 |
4 |
3 |
4 |
7 |
2 |
8 |
5 |
4 |
5 |
8 |
3 |
9 |
6 |
|
7 |
5 |
5 |
5 |
5 |
7 |
1 |
8 |
6 |
6 |
6 |
6 |
8 |
2 |
9 |
7 |
7 |
7 |
7 |
9 |
|
8 |
4 |
5 |
2 |
5 |
4 |
8 |
1 |
9 |
5 |
6 |
3 |
6 |
5 |
9 |
2 |
10 |
6 |
7 |
4 |
|
9 |
6 |
3 |
6 |
6 |
3 |
6 |
9 |
1 |
10 |
7 |
4 |
7 |
7 |
4 |
7 |
10 |
2 |
11 |
8 |
|
10 |
5 |
6 |
4 |
2 |
4 |
6 |
5 |
10 |
1 |
11 |
6 |
7 |
5 |
3 |
5 |
7 |
6 |
11 |
2 |
|
11 |
7 |
6 |
6 |
7 |
7 |
6 |
6 |
7 |
11 |
1 |
12 |
8 |
7 |
7 |
8 |
8 |
7 |
7 |
8 |
|
12 |
6 |
4 |
3 |
6 |
2 |
6 |
3 |
4 |
6 |
12 |
1 |
13 |
7 |
5 |
4 |
7 |
3 |
7 |
4 |
|
13 |
8 |
7 |
7 |
6 |
8 |
8 |
6 |
7 |
7 |
8 |
13 |
1 |
14 |
9 |
8 |
8 |
7 |
9 |
9 |
|
14 |
7 |
7 |
5 |
7 |
5 |
2 |
5 |
7 |
5 |
7 |
7 |
14 |
1 |
15 |
8 |
8 |
6 |
8 |
6 |
|
15 |
9 |
5 |
7 |
3 |
4 |
9 |
9 |
4 |
3 |
7 |
5 |
9 |
15 |
1 |
16 |
10 |
6 |
8 |
4 |
|
16 |
8 |
8 |
4 |
8 |
5 |
7 |
2 |
7 |
5 |
8 |
4 |
8 |
8 |
16 |
1 |
17 |
9 |
9 |
5 |
|
17 |
10 |
8 |
8 |
7 |
8 |
7 |
10 |
10 |
7 |
8 |
7 |
8 |
8 |
10 |
17 |
1 |
18 |
11 |
9 |
|
18 |
9 |
6 |
6 |
7 |
3 |
7 |
6 |
2 |
6 |
7 |
3 |
7 |
6 |
6 |
9 |
18 |
1 |
19 |
10 |
|
19 |
11 |
9 |
8 |
8 |
9 |
7 |
7 |
11 |
11 |
7 |
7 |
9 |
8 |
8 |
9 |
11 |
19 |
1 |
20 |
|
20 |
10 |
9 |
5 |
4 |
6 |
9 |
4 |
8 |
2 |
8 |
4 |
9 |
6 |
4 |
5 |
9 |
10 |
20 |
1 |
Tab. 1: Anzahl der benštigten Quadrate
Die Tabelle ist natźrlich symmetrisch und hat Einsen in der Hauptdiagonalen.
Unterhalb der Hauptdiagonalen erkennen wir ein Zahlendreieck, das seinerseits symmetrisch ist (Tab. 2).
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
4 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
3 |
2 |
3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
5 |
5 |
5 |
5 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
4 |
5 |
2 |
5 |
4 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
6 |
3 |
6 |
6 |
3 |
6 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
5 |
6 |
4 |
2 |
4 |
6 |
5 |
10 |
|
|
|
|
|
|
|
|
|
|
|
11 |
7 |
6 |
6 |
7 |
7 |
6 |
6 |
7 |
11 |
|
|
|
|
|
|
|
|
|
|
12 |
6 |
4 |
3 |
6 |
2 |
6 |
3 |
4 |
6 |
12 |
|
|
|
|
|
|
|
|
|
13 |
8 |
7 |
7 |
6 |
8 |
8 |
6 |
7 |
7 |
8 |
13 |
|
|
|
|
|
|
|
|
14 |
7 |
7 |
5 |
7 |
5 |
2 |
5 |
7 |
5 |
7 |
7 |
14 |
|
|
|
|
|
|
|
15 |
9 |
5 |
7 |
3 |
4 |
9 |
9 |
4 |
3 |
7 |
5 |
9 |
15 |
|
|
|
|
|
|
16 |
8 |
8 |
4 |
8 |
5 |
7 |
2 |
7 |
5 |
8 |
4 |
8 |
8 |
16 |
|
|
|
|
|
17 |
10 |
8 |
8 |
7 |
8 |
7 |
10 |
10 |
7 |
8 |
7 |
8 |
8 |
10 |
17 |
|
|
|
|
18 |
9 |
6 |
6 |
7 |
3 |
7 |
6 |
2 |
6 |
7 |
3 |
7 |
6 |
6 |
9 |
18 |
|
|
|
19 |
11 |
9 |
8 |
8 |
9 |
7 |
7 |
11 |
11 |
7 |
7 |
9 |
8 |
8 |
9 |
11 |
19 |
|
|
20 |
10 |
9 |
5 |
4 |
6 |
9 |
4 |
8 |
2 |
8 |
4 |
9 |
6 |
4 |
5 |
9 |
10 |
20 |
Tab. 2: Zahlendreieck
Dieses Zahlendreieck ist verwandt mit dem Zahlendreieck A110570.
4 Raster
Die
Abbildung 2 zeigt alle m × n-Rechtecke mit Unterteilungen fźr ![]() .
.

Abb. 2: Unterteilungen
Websites
The on-line encyclopedia of integer sequences (Abgerufen 28.8.2017):
The on-line encyclopedia of integer sequences (Abgerufen 28.8.2017):
Hans Walser: Quadratunterteilung (Abgerufen 28.8.2017):
www.walser-h-m.ch/hans/Miniaturen/Q/Quadratunterteilung2/Quadratunterteilung2.htm