Hans Walser, [20180108]
Rechter Winkel
1 Worum geht es?
Eine Figur, bei der ein rechter Winkel erscheint.
2 Die Figur
Wir
hŠngen zwei gleichsinnig kongruente rechtwinklige Dreiecke ![]() und
und ![]() im Punkt
im Punkt ![]() gelenkig
aneinander (Abb. 1). Es sind also zwei freie Parameter im Spiel: die Form des
rechtwinkligen Dreieckes und der Gelenkwinkel.
gelenkig
aneinander (Abb. 1). Es sind also zwei freie Parameter im Spiel: die Form des
rechtwinkligen Dreieckes und der Gelenkwinkel.
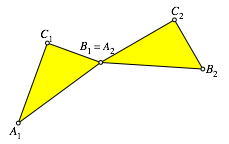
Abb. 1: Zwei rechtwinklige Dreiecke
Weiter
sei M der Mittelpunkt der Strecke ![]() (Abb. 2).
(Abb. 2).
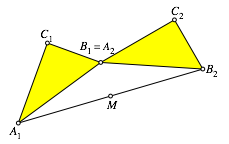
Abb. 2: Mittelpunkt
In dieser
Situation ist der Winkel ![]() ein
rechter (Abb. 3).
ein
rechter (Abb. 3).
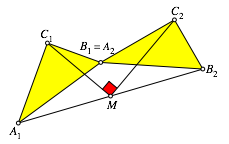
Abb. 3: Rechter Winkel
3 Beweis
Die Konfiguration ist ein Sonder- und Grenzfall des Theorems von E.V. [1] .
4 Variante
Durch Punktspiegelung an M erhalten wir folgende Variante: Wir setzen einem Rhombus kongruente rechtwinklige Dreiecke zyklisch an (Abb. 4).
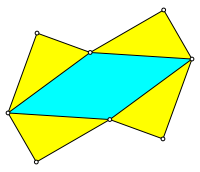
Abb. 4: Rhombus mit rechtwinkligen Dreiecken
Dann bilden die vier Ecken mit den rechten Winkeln ihrerseits einen Rhombus (Abb. 5).
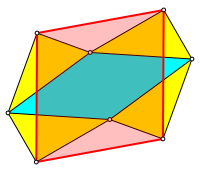
Abb. 5: Neuer Rhombus
Diese Version kann recht einfach bewiesen werden [2] .
Websites
[1] Walser: Symmetrie als Werkzeug (Abgerufen 08.01.2018):
http://www.wa lser-h-m.ch/hans/Vortraege/20170908/Presentation_Netz.pptx.pdf
[2] Walser: Rhomben (Abgerufen 08.01.2018):
http://www.walser-h-m.ch/hans/Miniaturen/R/Rhomben2/Rhomben2.htm