Hans Walser, [20110609a]
Im rechtwinkligen Dreieck
Eine Spielerei im
rechtwinkligen Dreieck.
1
Gleich lange Strecken
Zu einem rechtwinkligen
Dreieck zeichnen wir die beiden Kathetenquadrate und verbinden Ecken gemŠ§ Abbildung
1.
Dann sind die beiden
roten Strecken gleich lang.
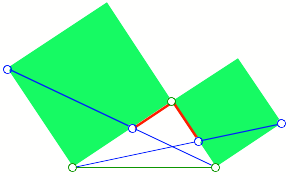
Abb. 1: Rote Strecken
gleich lang
2
Ein weiteres Quadrat
Wir ergŠnzen die beiden
roten Strecken zum Quadrat. Dann liegt die vierte Ecke auf der Hypotenuse (Abb.
2).
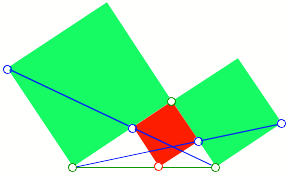
Abb. 2: Quadratecke auf
Hypotenuse
3
Beweise
Wir verwenden die fźr
die rechtwinkligen Dreiecke źblichen Bezeichnungen und ergŠnzen gemŠ§ Abbildung
3. Die Beweise laufen nun mit StrahlensŠtzen und VerhŠltnissen.
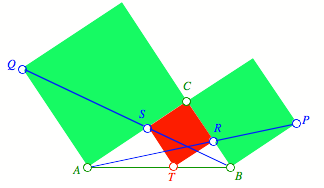
Abb. 3: Bezeichnungen
Auf Grund der
StrahlensŠtze ist 
. Wegen 
folgt 
. Analog (und schon aus formalen Symmetriegrźnden) wird 
. Es ist also 
.
Wir zeichnen nun eine
Parallele zu AC durch R. Diese schneidet die Hypotenuse in einem Punkt 
, fźr den gilt:
Analog erhalten wir
durch eine Parallele zu BC durch S einen Schnittpunkt 
mit:
Somit ist 
.
4
Direkter Zugang
Wir passen das rote
Quadrat ins rechtwinklige Dreieck ein und strecken von A aus auf das Kathetenquadrat źber der Seite a (Abb. 4).
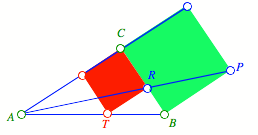
Abb. 4: Strecken des
roten Quadrates
Analog verfahren wir
mit dem zweiten Kathetenquadrat.
5
Verallgemeinerung: Variante mit Rhomben
Wir setzen einem
beliebigen Dreieck auf den Seiten a und b Rhomben mit dem Winkel 
gemŠ§ Abbildung
5 auf.
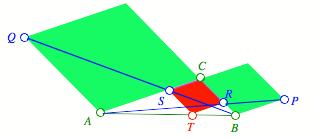
Abb. 5: Aufsetzen von
Rhomben