1 Problemstellung

Für welches rechtwinklige Dreieck ist die eingezeichnete Verbindung der Kathetenquadratecken (Abb. 1) parallel zur Hypotenuse des Dreieckes?

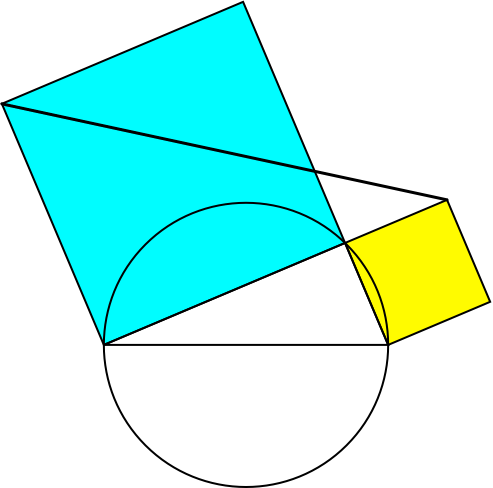
Abb. 1: Verbindung von Kathetenquadratecken

2 Animation

Wir sehen, dass es zwei Positionen mit paralleler Verbindung gibt (Abb. 2).

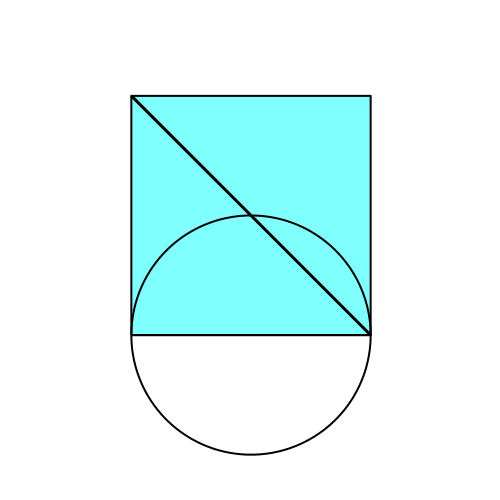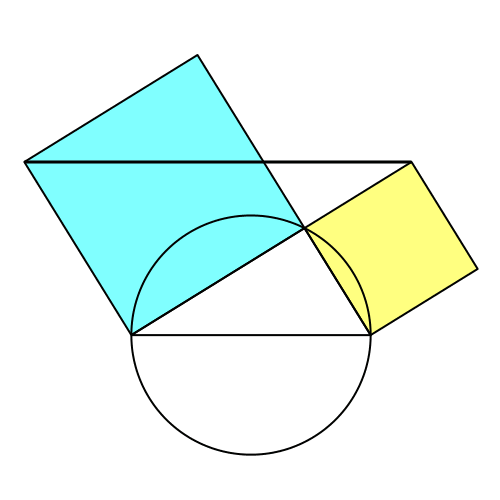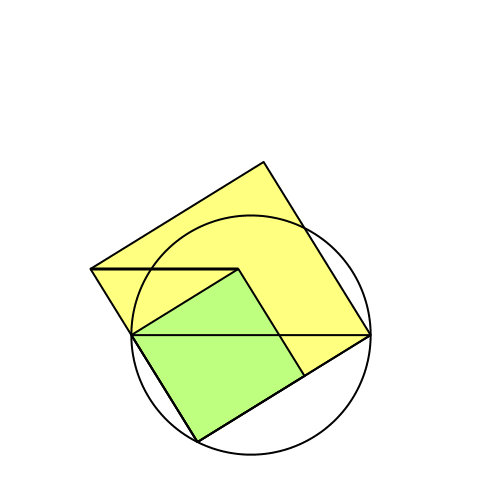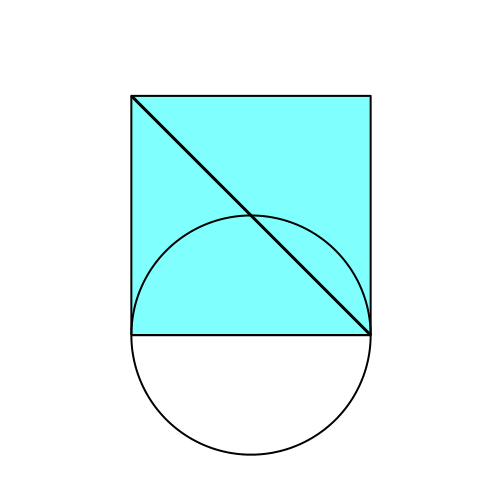
Abb. 2: Animation

3 Bearbeitung

Wir arbeiten mit den Bezeichnungen der Abbildung 3.

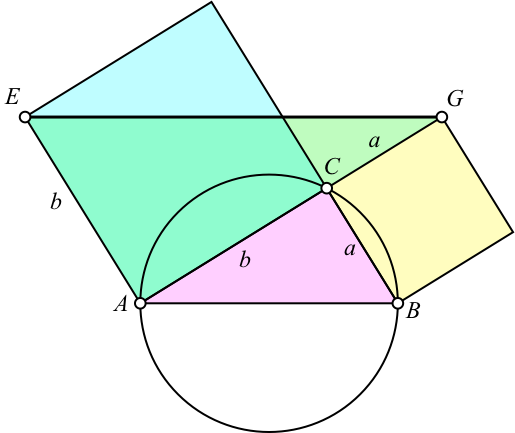
Abb. 3: Bezeichnungen

Im Sonderfall der Problemstellung sind die beiden Dreiecke ABC und GEA ähnlich. Daher ist:

b/a = (a + b)/b

Daraus ergibt sich die quadratische Gleichung für b/a:

(b/a)² = 1 + b/a

Die positive Lösung ist: b/a = Φ. Dabei ist Φ = (1 + √5)/2 ≈ 1.618 der Goldene Schnitt.

In der Figur haben wir an verschiedenen Orten die Relation Major zu Minor (exemplarisch in Abb. 4).

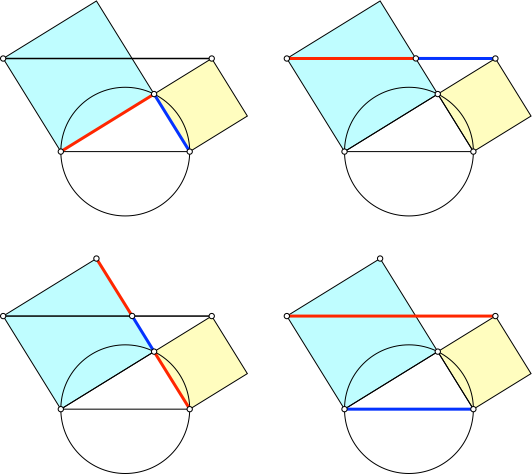
Abb. 4: Major und Minor

4 Ein Schnittpunkt

Wir spiegeln das rechtwinklige Dreieck an der gemeinsamen Diagonale der beiden Kathetenquadrate (Abb. 5). Dann ist die Höhe im einen Dreieck auch Schwerlinie im anderen und umgekehrt. Dies gilt allerdings nicht nur in unserem speziellen rechtwinkligen Dreieck, sondern in jedem rechtwinkligen Dreieck. In unserem Sonderfall erhalten wir nun aber einen gemeinsamen Schnittpunkt von drei Geraden gemäß Abbildung 5.

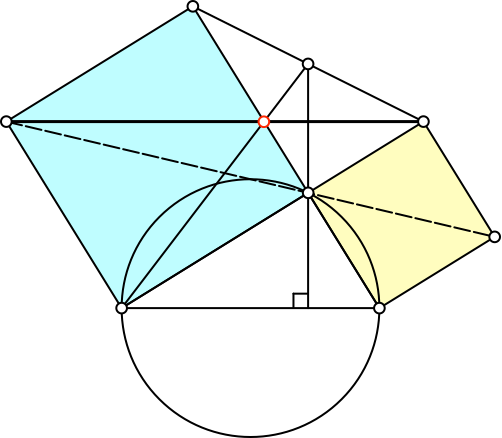
Abb. 5: Ein Schnittpunkt

5 Die zweite Lösung

Die Animation (Abb. 2) zeigt eine zweite Lösung (das rechtwinklige Dreieck ist unten, die Kathetenquadrate sind auf der Innenseite des Dreiecks). Auch hier finden wir den Goldenen Schnitt (Abb. 6).

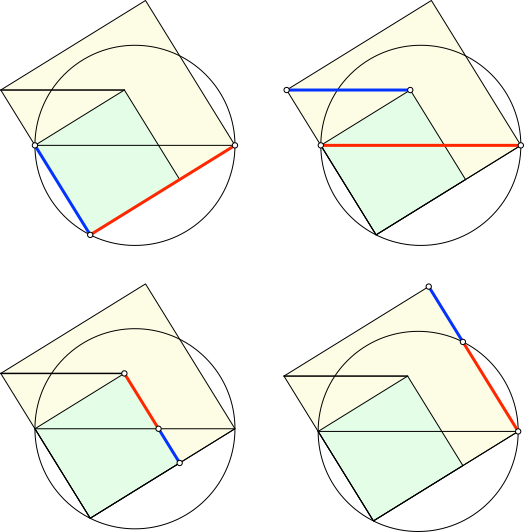
Abb. 6: Goldener Schnitt in der zweiten Lösung