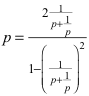Hans Walser, [20230919]
Rechtwinkliges Dreieck und Goldener Schnitt
Idee und Anregung: Maik Rentsch
1 Worum es geht
Ein Spiel im rechtwinkligen Dreieck mit Inkreis und umbeschriebenen Rechteck führt zum Goldenen Schnitt.
2 Rechtwinkliges Dreieck und umbeschriebenes Rechteck
Wir passen ein rechtwinkliges Dreieck mit seinem Inkreis in ein Rechteck ein. Die Hypotenuse des Dreiecks ist die eine Seite des Rechtecks, die Dreieckshöhe senkrecht dazu die andere (Abb. 1).
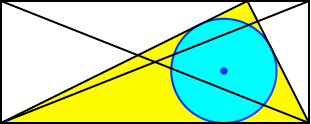
Abb. 1: Dreieck im Rechteck
Die Frage ist, für welches rechtwinklige Dreieck die eine oder andere Diagonale des Rechteckes durch den Inkreismittelpunkt verläuft (Abb. 2). Auf Grund der Animation vermuten wir zwei symmetrische Lösungen.
Abb. 2: Veränderung des rechtwinkligen Dreiecks
3 Bearbeitung
Wir normieren die Dreieckshöhe senkrecht zur Hypotenuse auf 1. Wegen dem Höhensatz sind damit die beiden Hypotenusenabschnitte Kehrwerte voneinander.
Wir verwenden die Bezeichnungen der Abbildung 3.
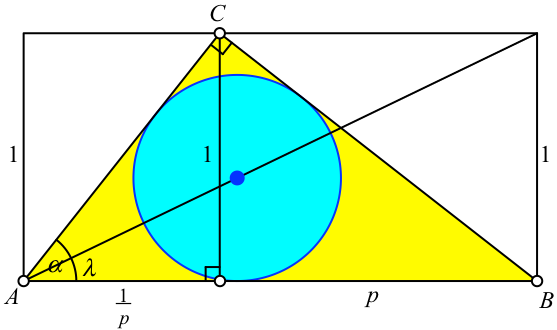
Abb. 3: Bezeichnungen
Zunächst ist:
![]()
![]()
Aus dem Additionstheorem für den Tangens ergibt sich:
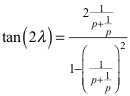
Für unsere Fragestellung muss die Rechteckdiagonale auch Winkelhalbierende des Dreiecks sein, also α = 2 λ und damit:
Diese Bedingung kann umgeformt werden zu: p4 – p2 – 1 = 0. Die positive Lösung dieser biquadratischen Gleichung ist p = √Φ ≈ 1.272. Dabei ist Φ der Goldene Schnitt: Φ = (1 + √5)/2 ≈ 1.618
Es ist dann 1/p = 1/√Φ ≈ 0.786. Weiter ist p : (1/p) = Φ.
In der Abbildung 4 ist der Goldene Schnitt mit Major und Minor illustriert.
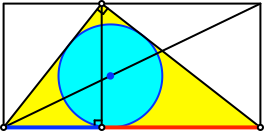
Abb. 4: Major und Minor
Wir finden den Goldenen Schnitt auch andernorts (Abb. 5 und 6).
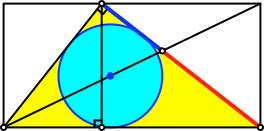
Abb. 5: Major und Minor
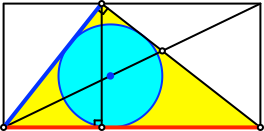
Abb. 6: Major und Minor
4 Quadrat einpassen
Wir passen am linken Rand des Rechteckes ein Quadrat mit seinen Diagonalen ein (Abb. 7).

Abb. 7: Quadrat einpassen
Nun drehen wir das Quadrat um die linke untere Ecke, bis die eine Quadratdiagonale auf die Rechteckdiagonale zu liegen kommt (Abb. 8).
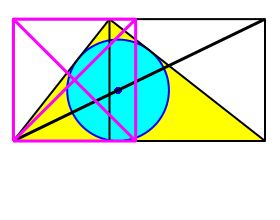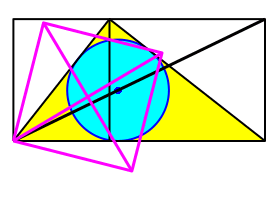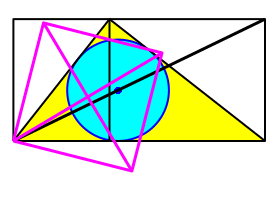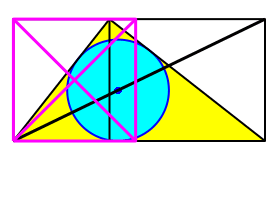
Abb. 8: Quadrat drehen
In der Endlage (Abb. 9) kommt die dem Drehpunkt gegenüberliegende Quadratecke auf den Teilpunkt im Goldenen Schnitt der dem Drehpunkt gegenüberliegenden Kathete des Dreiecks zu liegen.
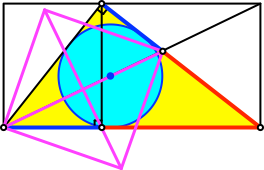
Abb. 9: Endlage
Die andere Quadratdiagonale verläuft durch den Höhenfußpunkt des Dreiecks und damit durch den Teilpunkt im goldenen Schnitt der Hypotenuse.
Weblink
Hans Walser: Rechtwinkliges Dreieck und Goldener Schnitt