Hans Walser, [20150901]

RegelmŠ§ige Sterne

1     Worum geht es?

Die regelmŠ§igen Vielecke kšnnen auch mit SelbstŸberlagerung (ãŸberschlagenÒ) gezeichnet werden.

Die Abbildung 1 zeigt die Situation bei Siebenecken. Alle drei Figuren haben dieselbe SeitenlŠnge.

 

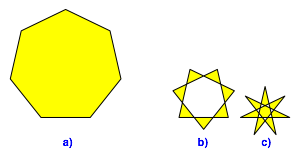
Abb. 1: RegelmŠ§ige Siebenecke

 

Das regelmŠ§ige Siebeneck der Abbildung 1a wird mit dem SchlŠfli-Symbol  oder auch  bezeichnet. Das regelmŠ§ige Siebeneck hat den Au§enwinkel .

Der Stern der Abbildung 1b hat das SchlŠfli-Symbol . Dies kann verschieden interpretiert werden. Wir kšnnen uns sieben gleichmŠ§ig auf einem Kreis verteilte Punkte vorstellen, bei denen nun jeder zweite ausgewŠhlt wird. Oder wir kšnnen sagen, dass der Streckenzug zweimal um das Zentrum herumlŠuft, bevor er sich schlie§t. Daher hat dieser Stern den Au§enwinkel . Die einzelnen Strecken des Streckenzuges haben dabei alle die gleiche LŠnge.

Beim Stern  der Abbildung 1c wird jeder dritte Punkt ausgewŠhlt, und der Streckenzug lŠuft dreimal um das Zentrum. Der Au§enwinkel ist .

Wir sehen, wie die Verallgemeinerung  lŠuft.

2     Probleme mit Teilern

Ein Problem tritt auf, wenn k ein Teiler von n ist. Beispiel: in  kšnnen wir verschieden vorgehen. Wenn wir jeden dritten Punkt nehmen, erhalten wir ein dreimal durchlaufenes Quadrat (Abb. 2a). Die vier Ecken mŸssen jeder dreimal gezŠhlt werden. So kommen wir schon auf 12 Ecken, aber sie sind nicht sichtbar.

 

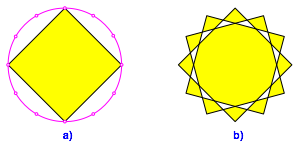
Abb. 2: Der Stern {12/3}

 

Wir kšnnen aber auch ein Quadrat um 30¡ und um 60¡ verdrehen (Abb. 2b). Dann wird jedenfalls das Zentrum auch dreimal umfahren. Hingegen wird es etwas schwieriger, dieses dreimalige Umfahren mit einem geschlossenen Streckenzug zu bewerkstelligen. Die Abbildung 3a zeigt eine Lšsung. Wir mŸssen bei zwei Kreuzungen abbiegen statt geradeaus fahren. Diese Lšsung hat allerdings den Nachteil, dass die Strecken des Streckenzuges nicht mehr gleich lang sind. Die Abbildung 3b zeigt eine andere Lšsung. Wie viele Lšsungen gibt es?

 

Abb. 3: ZusammenhŠngende Kurven

 

Im Folgenden wird die Version der Abbildung 2b verwendet.

3     Fluchtlinien

In der Abbildung 1 sind die drei Figuren mit ungleichen ZwischenrŠumen angegeben. Dies deshalb, weil wir so zwei ãFluchtlinienÒ haben (Abb. 4).

 

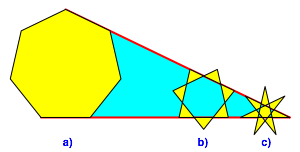
Abb. 4: Fluchtlinien

 

4     Bildergalerie

FŸr die Eckenzahlen n = 3 und n = 4 gibt es keine Sterne.

FŸr die Eckenzahl n = 5 gibt es neben dem Pentagon das Pentagramm (Drudenfu§).

 

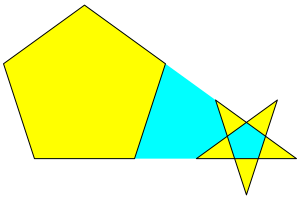
Abb. 5: Eckenzahl 5

 

FŸr die Eckenzahl n = 6 wird die Figur kompakt (Abb. 6). Dieses PhŠnomen tritt bei geraden Eckenzahlen auf.

 

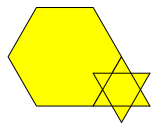
Abb. 6: Kompaktlšsung

 

Die Abbildung 7 zeigt nochmals den Fall fŸr die Eckenzahl n = 7. Wir haben zum ersten Mal zwei Sterne.

 

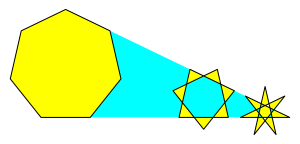
Abb. 7: Eckenzahl 7

 

Bei der Eckenzahl n = 8 gibt es wieder eine Kompaktlšsung (Abb. 8).

 

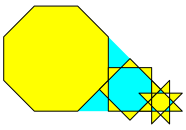
Abb. 8: Eckenzahl 8

 

Bei der Eckenzahl n = 9 gibt es drei Sterne (Abb. 9).

Die Anzahl der Sterne ist allgemein .

 

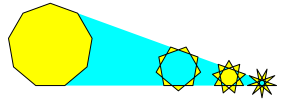
Abb. 9: Eckenzahl 9

 

Das GedrŠnge bei der Eckenzahl n = 10 war zu erwarten (Abb. 10).

 

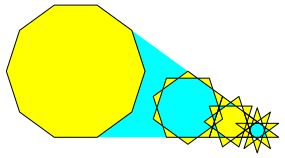
Abb. 10: Eckenzahl 10

 

Bei der Eckenzahl n = 11 erscheint ein vierter Stern (Abb. 11).

 

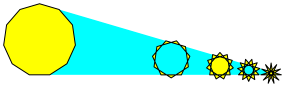
Abb. 11: Eckenzahl 11

 

Schlie§lich bei der Eckenzahl n = 12 nochmals eine Kompaktsituation (Abb. 12):

 

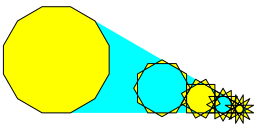
Abb. 12: Eckenzahl 12

 

5     Sternbilder

 

Abb. 13: Cluster mit FŸnfecksternen

 

Abb. 14: Cluster mit Siebenecksternen

 

Abb. 15: Zwšlfecksterne