Hans Walser, [20140417]
Regulre Polygone gerader Eckenzahl
1 Flchengleichheiten
Bei regulren Polygonen gerader Eckenzahl gelten die in der Abbildung 1 angedeuteten Flchenbeziehungen.

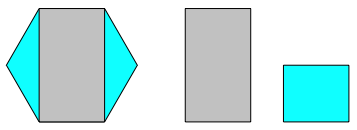
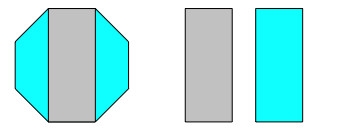




Abb. 1: Flchenbeziehungen
Diese Beziehungen lassen sich durch Nachrechnen verifizieren. Fr ein 2m-Eck erhalten wir einerseits den gesamten Flcheninhalt
![]()
und andererseits fr das Rechteck den Flcheninhalt
![]() .
.
Somit ergibt sich das Flchenverhltnis
![]() .
.
Wenn m eine gerade Zahl ist, also die Eckenzahl des Polygons eine Viererzahl, geht es auf.
Falls m eine ungerade Zahl ist, ergibt sich ein halbzahliges Verhltnis. Die Eckenzahl des Polygons ist dann 6, 10, 14, ... . Euler (1782) bezeichnete diese Zahlen als nombres impairement pairs. Diese etwas merkwrdige Formulierung wurde von meinen Studierenden etwa so interpretiert: Diese Zahlen setzen sich aus einer ungeraden Anzahl von Paaren zusammen. Sie besetzen in der Liste der geraden Zahlen die ungeraden Positionen. Sie sind die Summe von zwei ungeraden Zahlen.
2 Zerlegungsbeweise
Die Abbildung 2 zeigt einheitliche Zerlegungsbeweise.





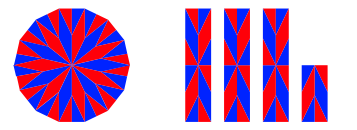

Abb. 2: Zerlegungsbeweise
Die Abbildung 3 zeigt dasselbe in einer anderen Frbung.




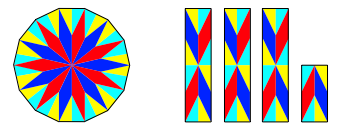
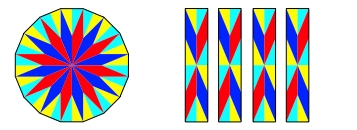
Abb. 3: Sterne
Die Abbildung 4 zeigt eine weitere Variante.

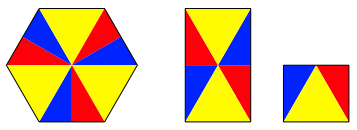
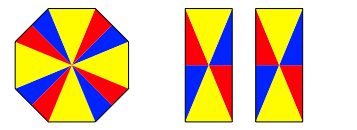
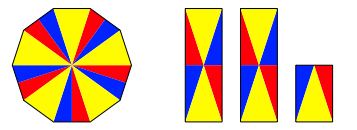
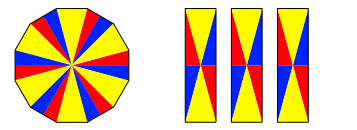
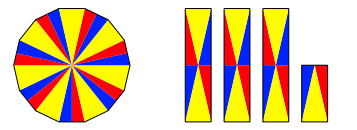
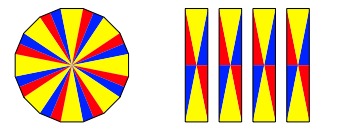
Abb. 4: Variante
Natrlich gibt es noch viele andere Zerlegungsbeweise.
Literatur
Euler, L.
(1782): Recherches sur une
nouvelle espce de quarrs magiques. Opera
Omnia, Series 1, Volume 7, 291-392. Enestrm Index 530.