1 What about

We draw circles of equal size and inscribe them regular polygons and regular star polygons. With the sides of these figures we try to form right triangles.

2 Possible solutions

A brute force approach indicates the conjecture that there are only fife solutions, two of them with stars (Tab. 1).

First polygon	Second polygon	Third polygon
6	4	3
6	6	4
10	6	5
10	10/3	3
6	10/3	5/2

Tab. 1: Solutions

2.1 Hexagon, square, and triangle

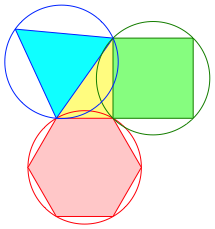
Fig. 1: 6, 4, 3

The right triangle is half a rectangle in the DIN format (European paper format).

2.2 Two hexagons and a square

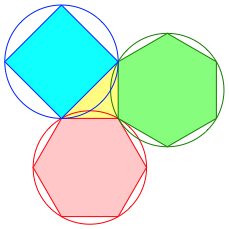
Fig. 2: 6, 6, 4

The right triangle is half a square

2.3 Decagon, hexagon, and pentagon

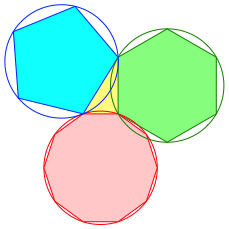
Fig. 3: 10, 6, 5

The right triangle is half a golden rectangle.

2.4 Decagon, decagonal star, and triangle

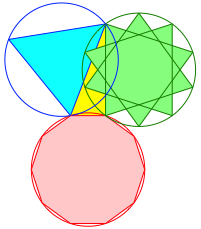
Fig. 4: 10, 10/3, 3

The right triangle is half a long golden rectangle with sides and .

2.5 Hexagon, decagonal star, and pentagram

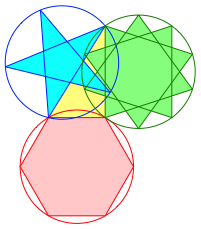
Fig. 5: 6, 10/3, 5/2

The right triangle is half a golden rectangle.

3 Two-gons

If we allow regular two-gons, i. e. diameters, we get infinitely many solutions. Table 2 gives the first solutions. The two-gon is always the third polygon.

First polygon	Second polygon	Third polygon
4	4	2
6	3	2
6	4	3
6	6	4
8	8/3	2
10	5/2	2
10	6	5
10	10/3	3
5	10/3	2
6	10/3	5/2
12	12/5	2
14	7/3	2
14/3	7/2	2
7	14/5	2
16	16/7	2
16/3	16/5	2
16	16/7	2
18	9/4	2
9/2	18/5	2
9	18/7	2
20	20/9	2
20/3	20/7	2

Tab. 2: Two-gons included

3.1 6, 3, 2

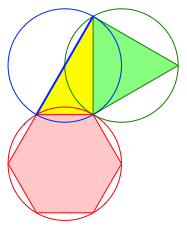
Fig. 6: 6, 3, 2

3.2 14/3, 7/2, 2

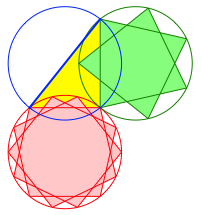
Fig. 7: 14/3, 7/2, 2

3.3 General case

One of the two first polygons is arbitrary. The second polygon is such that each side is orthogonal to a side of the first polygon. The circles of the two polygons are tangent.