Hans Walser, [20200619]
Regelmäßige Vielecke
1 Worum geht es?
Eine Schließungsfigur mit regelmäßigen Vielecken.
2 Einführung
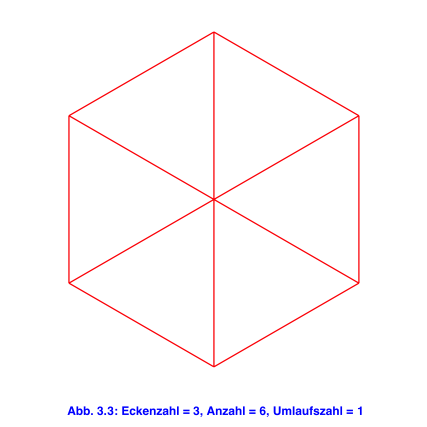
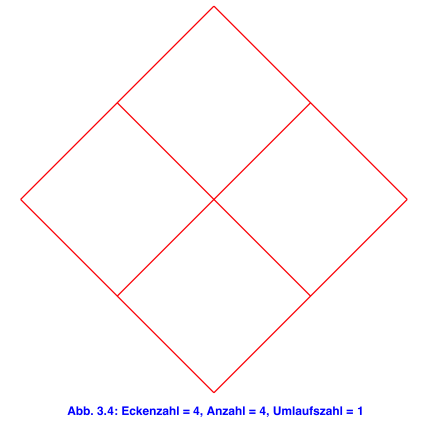
Wir können sechs regelmäßige Dreiecke (Abb. 1a), vier Quadrate (Abb. 1b) oder drei regelmäßige Sechsecke (Abb. 1c) an einer Ecke zusammenfügen, so dass es nach einem Umlauf aufgeht.
Abb. 1: Aneinanderfügen von regelmäßigen Vielecken
Bei regelmäßigen Fünfecken geht es nicht mehr so schlank.
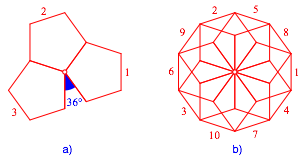
Abb. 2: Regelmäßige Fünfecke
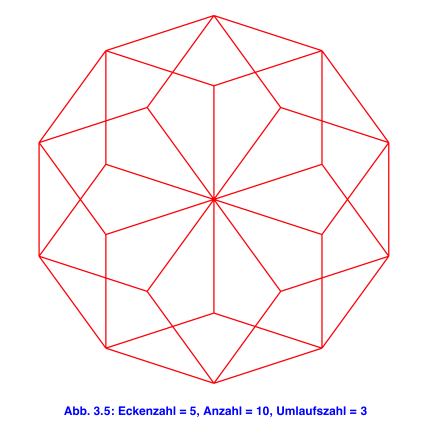
Nach drei Fünfecken bleibt eine Lücke von 36° übrig (Abb. 2a), die sich nicht mehr mit einem weiteren Fünfeck schließen lässt. Wenn wir jedoch unbeirrt weiterfahren, kommen wir nach insgesamt zehn Fünfecken und drei Umläufen zurück (Abb. 2b). Wir haben also eine Schließungsfigur.
Tatsächlich ist es so, dass Dreieck, Quadrat und Sechseck (Abb. 1) die einzigen konvexen Vielecke sind, die sich nach einem Umlauf schließen.
3 Beispiele
Im Folgenden systematisch Beispiele. Es sind jeweils die Eckenzahl n ≥ 3 des regelmäßigen Vieleckes, die Anzahl a der benötigten Vielecke und die Umlaufszahl u angegeben.
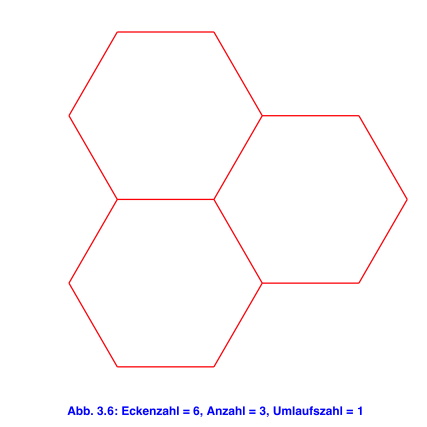
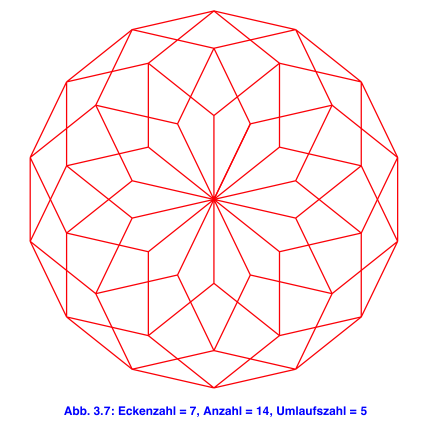
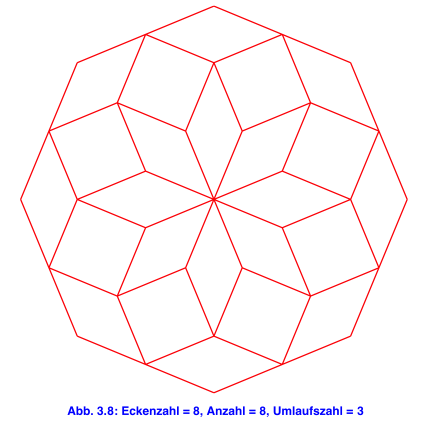
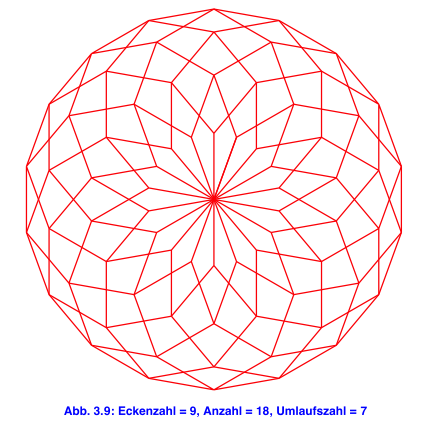
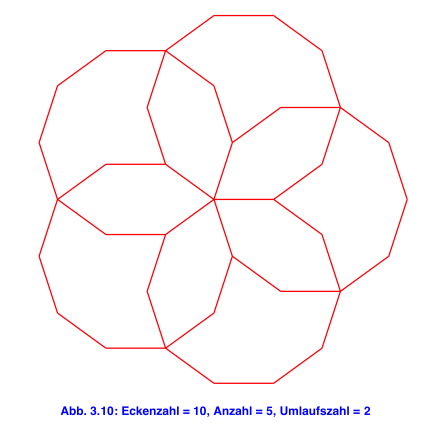
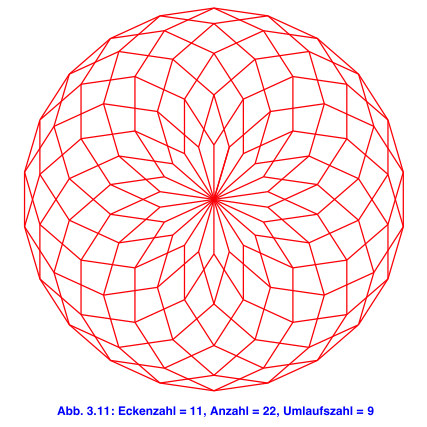
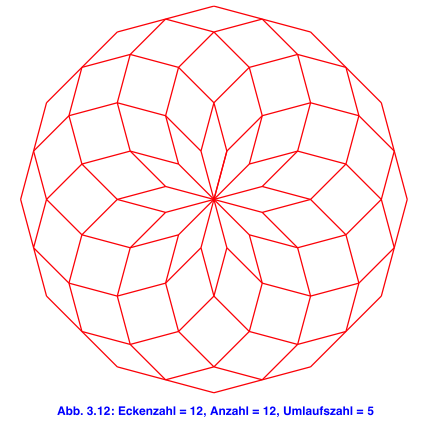
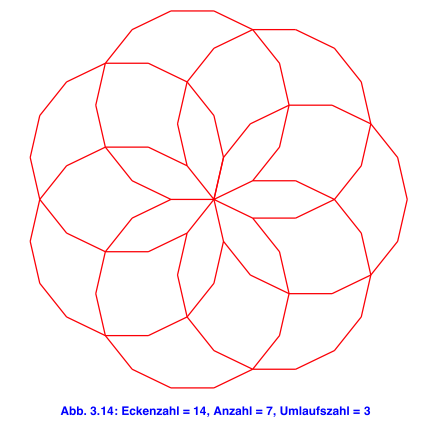
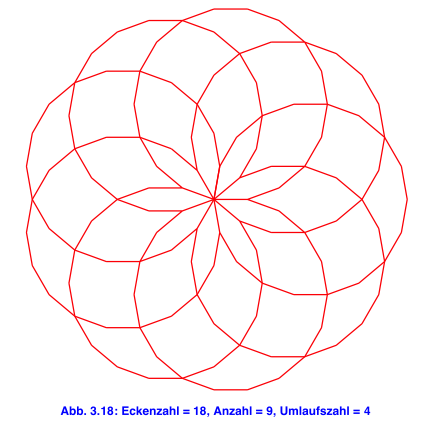
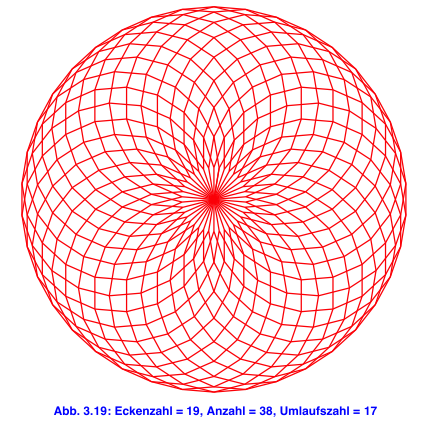
4 Anzahl und Umlaufszahl
Der
Innenwinkel eines n-Ecks ist 
. Bei jedem Anfügen eines n-Eckes wird also um diesen Winkel weitergedreht. Die
Schließungsbedingung führt auf:
(1)
Weiter müssen a und u teilerfremd sein (um Ehrenrunden zu vermeiden). Somit ergibt sich für gegebenes n:
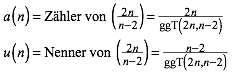(2)
Dadurch,
dass wir zuerst den Bruch 
bilden und
kürzen und erst anschließend in Zähler und Nenner aufteilen, erreichen wir,
dass a und u teilerfremd sind.
|
n |
a |
u |
|
n |
a |
u |
|
|
|
|
|
21 |
42 |
19 |
|
|
|
|
|
22 |
11 |
5 |
|
3 |
6 |
1 |
|
23 |
46 |
21 |
|
4 |
4 |
1 |
|
24 |
24 |
11 |
|
5 |
10 |
3 |
|
25 |
50 |
23 |
|
6 |
3 |
1 |
|
26 |
13 |
6 |
|
7 |
14 |
5 |
|
27 |
54 |
25 |
|
8 |
8 |
3 |
|
28 |
28 |
13 |
|
9 |
18 |
7 |
|
29 |
58 |
27 |
|
10 |
5 |
2 |
|
30 |
15 |
7 |
|
11 |
22 |
9 |
|
31 |
62 |
29 |
|
12 |
12 |
5 |
|
32 |
32 |
15 |
|
13 |
26 |
11 |
|
33 |
66 |
31 |
|
14 |
7 |
3 |
|
34 |
17 |
8 |
|
15 |
30 |
13 |
|
35 |
70 |
33 |
|
16 |
16 |
7 |
|
36 |
36 |
17 |
|
17 |
34 |
15 |
|
37 |
74 |
35 |
|
18 |
9 |
4 |
|
38 |
19 |
9 |
|
19 |
38 |
17 |
|
39 |
78 |
37 |
|
20 |
20 |
9 |
|
40 |
40 |
19 |
Tab. 1: Eckenzahl, Anzahl, Umlaufszahl
5 Rationales
Wenn wir
in (2) die rationale Zahl 
einsetzen,
ergibt sich:
(3)
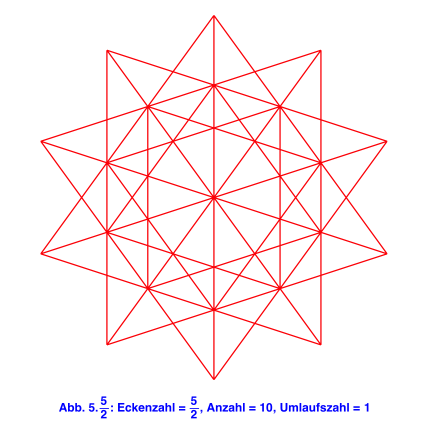
Beim 
haben wir
also mit 10 Exemplaren schon nach einem Umlauf eine Schließungsfigur. Das 
ist das
Pentagramm (Abb. 4a). Die Zahl 2 im Nenner bedeutet, dass auf dem Umkreis
jeweils jede zweite Ecke genommen wird.
Das angefügte zweite Pentagramm (Abb. 4b) überlappt sich teilweise mit dem ersten.
Abb. 4: Pentagramm
Im Folgenden einige Beispiele dieser Art.
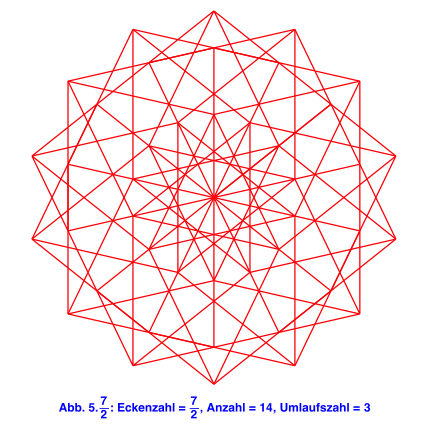
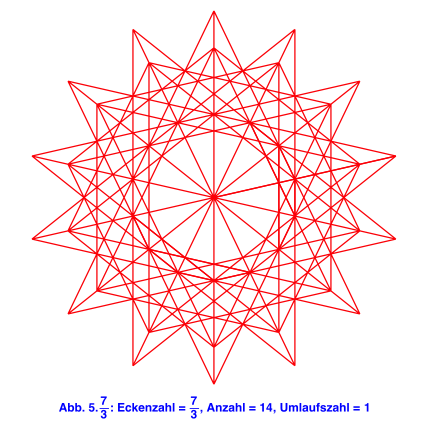
Websites
[1] The on-line encyclopedia of integer sequences