Hans Walser, [20150106]
Regelm§ige Zahlenvielecke
1 Worum es geht
Mit Hilfe der Bi-, Tri- und Tetranomialzahlen werden Zahlenanordnungen im regelm§igen Dreieck, im Quadrat und im regelm§igen Sechseck konstruiert.
2 Binomialkoeffizienten
2.1 Ausgangslage
Die Abbildung 1 zeigt oben Mitte das Pascalsche Dreieck der Binomialkoeffizienten. Das Dreieck ist unten offen, in der Abbildung 1 ist nur die Situation bis zur Reihe Nummer 6 (Nummerierung beginnt mit null) angegeben. Das Dreieck hat eine senkrechte Symmetrieachse.
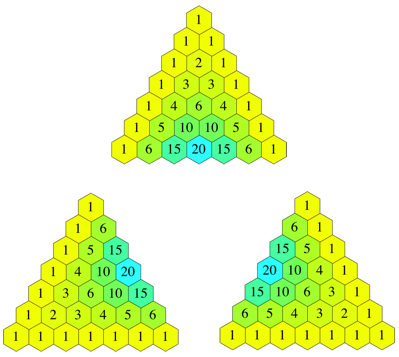
Abb. 1: Binomialkoeffizienten
In der Abbildung 1 sind unten zwei weitere Dispositionen des Pascalschen Dreiecks der Binomialkoeffizienten angegeben.
2.2 berlagerung
Die Idee ist nun, diese drei Dreiecke zu berlagern. Die berlagerungsfigur hat dann die Symmetrien des regelm§igen Dreiecks.
Dann haben wir in jedem Feld drei Zahlen.
Wir knnen diese drei Zahlen auf verschiedene Arten miteinander verrechnen. Um die Symmetrie zu erhalten, mssen die ternren Rechenoperationen gegenber Permutationen der drei Zahlen invariant sein. Als Beispiele bieten sich etwa an:
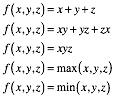
2.3 Beispiele
2.3.1 Produkt
Wir arbeiten mit dem Produkt der drei Zahlen. Die Abbildung 2 zeigt die Situation fr verschieden gro§e Dreiecke. Wir erkennen an den Rndern die gewhnlichen Binomialkoeffizienten.
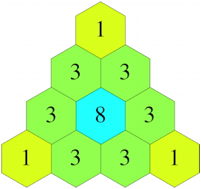
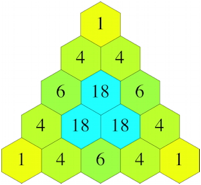
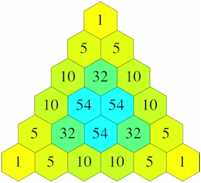
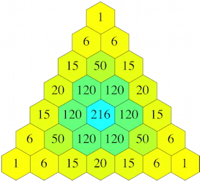
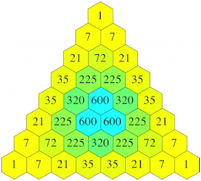
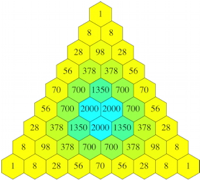
Abb. 2: Produkte
2.3.2 Summe
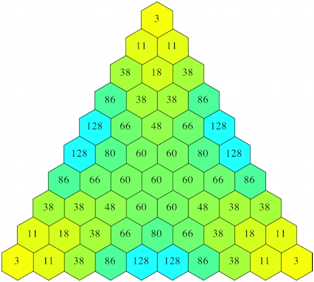
Abb. 3: Summe
2.3.3 Summe der Produkte von je zwei Zahlen
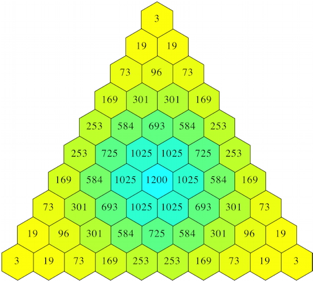
Abb. 4: Summe der Produkte von je zwei Zahlen
2.3.4 Maximum
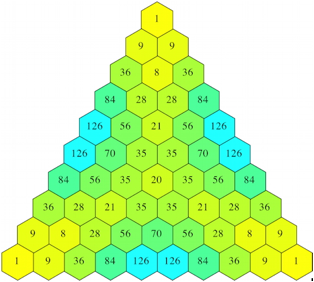
Abb. 5: Maximum der drei Zahlen
2.3.5 Minimum
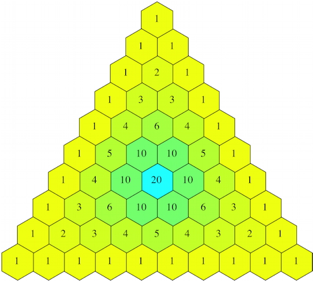
Abb. 6: Minimum
2.4 Frbung
In der Abbildung 7 wird mit dem Produkt gearbeitet. Die Felder sind gefrbt je nachdem, welchen Wert das Produkt modulo 8 annimmt (Tab. 1).
|
x mod 8 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
RGB |
0, 0, 0 |
1, 0, 0 |
0, 1, 0 |
1, 1, 0 |
0, 0, 1 |
1, 0, 1 |
0, 1, 1 |
1, 1, 1 |
|
Farbe |
|
|
|
|
|
|
|
|
Tab. 1: Farbcode
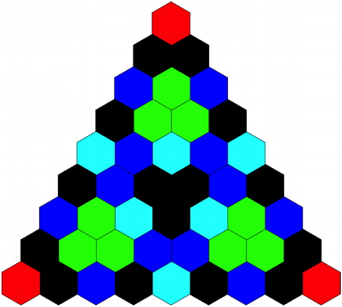
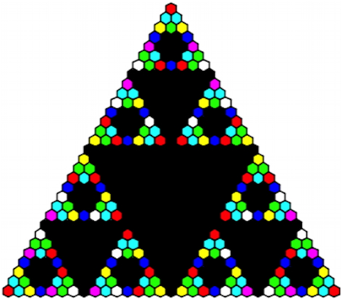
Abb. 7: Frbung modulo 8
Eine Vernderung der Ausma§e des Dreieckes verndert die Farben.
2.5 Parkettierung
Die Dreiecke haben keinen glatten Rand. Das macht Probleme bei einer Parkettierung.
Wenn wir mit zwei Farben auskommen wollen, mssen wir Lcken einbauen (Abb. 8).
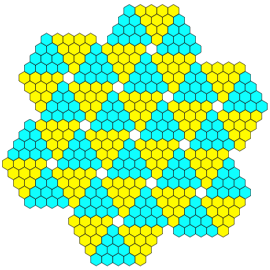
Abb. 8: Parkettierung mit Lcken
Die Mittelpunkte der Parkettsteine bilden ein regelm§iges Sechseckraster (Abb. 9).
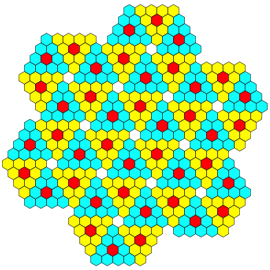
Abb. 9: Regelm§iges Sechseckraster
Bei vier Farben geht es lckenlos (Abb. 10).
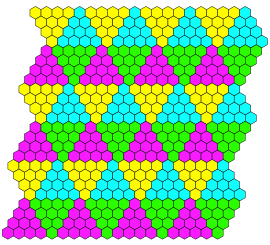
Abb. 10: Lckenlose Parkettierung
Allerdings bilden die Mittelpunkte der Parkettsteine nun kein regelm§iges Sechseckraster mehr (Abb. 11). Die Sechsecke sind affin verzerrt.
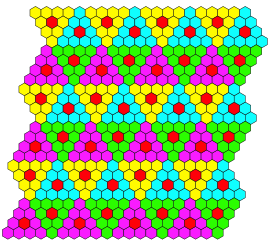
Abb. 11: Kein regelm§iges Sechseckraster
3 Trinomialkoeffizienten
3.1 Die Koeffizienten
Wir
arbeiten mit den Koeffizienten von ![]() .
Es ist:
.
Es ist:
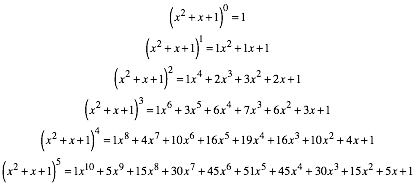
Diese Trinomialkoeffizienten knnen symmetrisch in einem Karoraster angeordnet werden gem§ Abbildung 12. Wir haben ein nach unten offenes Zahlendreieck.
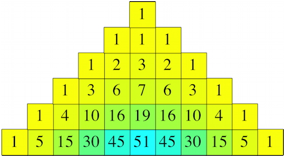
Abb. 12: Trinomialkoeffizienten
Jede Zahl ist die Summe der drei Zahlen, welche in der oberen Reihe direkt darber sowie links und rechts davon stehen.
3.2 berlagerung
Die Abbildung 13 zeigt nun quadratische Ausschnitte aus dem Dreieck der Trinomialkoeffizienten in vier verschiedenen Anordnungen.
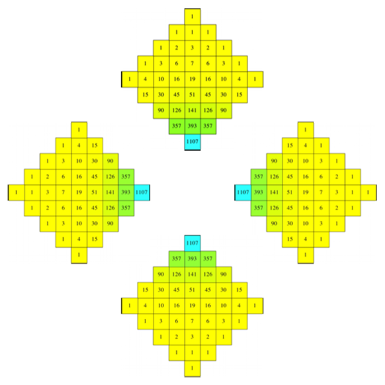
Abb. 13: Ausschnitte
Wir knnen nun die vier Quadrate berlagern und in jedem Feld die vier Zahlen geeignet verrechnen.
Die Abbildungen 14 und 15 zeigen berlagerungen mit Summen und Produkten.
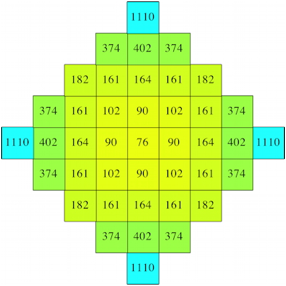
Abb. 14: Summen
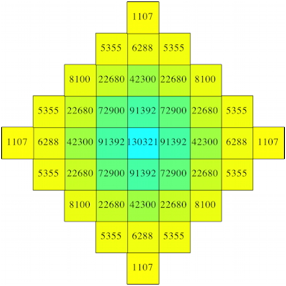
Abb. 15: Produkte
3.3 Frbung
Wir arbeiten wieder mit einer modularen Frbung gem§ Tabelle 1. In den Beispielen der Abbildung 16 ist mit Summen gearbeitet worden.
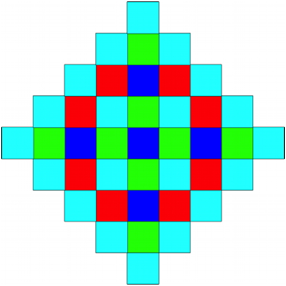

Abb. 16: Frbung modulo 8
3.4 Parkettierung
Die Parkettierung macht keine Probleme (Abb. 17). Die Mittelpunkte der Parkettsteine bilden ein Quadratraster, das allerdings etwas schrg in der Landschaft hngt.


Abb. 17: Parkettierung
4 Tetranomialkoeffizienten
4.1 Die Koeffizienten
Wir
arbeiten mit den Koeffizienten von ![]() .
Es ist:
.
Es ist:
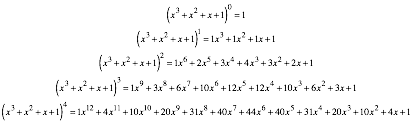
Die Koeffizienten passen nun wieder in ein Hexagonalraster (Abb. 18).
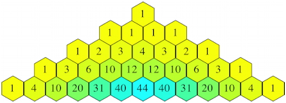
Abb. 18: Tetranomialkoeffizienten
Jede Zahl ist die Summe der vier Zahlen, die in der Reihe darber symmetrisch oberhalb der Zahl positioniert sind.
4.2 berlagerung
Die Abbildung 19 zeigt einen hexagonalen Ausschnitt aus dem Dreieck der Tetranomialkoeffizienten.
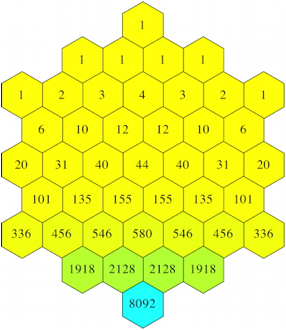
Abb. 19: Hexagonaler Ausschnitt
Die Abbildung 20 zeigt die sechs Anordnungen fr die berlagerung.

Abb. 20: Bereitstellung zur berlagerung
Die Abbildungen 21 und 22 zeigen Summe und Produkt in der berlagerung.
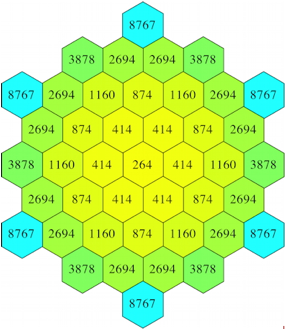
Abb. 21: Summe
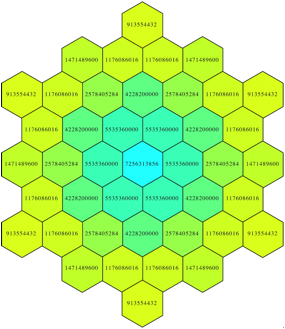
Abb. 22: Produkt
4.3 Frbung
Die Abbildungen 23 und 24 zeigen Frbungen gem§ Tabelle 1 fr Summe und Produkt.
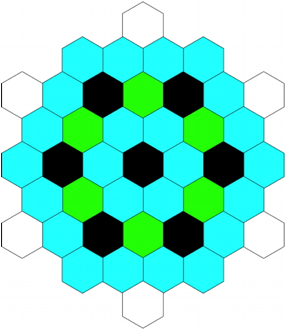
Abb. 23: Frbung, Summe

Abb. 24: Frbung, Produkt
Sobald drei Primfaktoren 2 vorkommen, wird es schwarz.
4.4 Parkettierung
Die Parkettierung geht gut, braucht aber drei Farben (Abb. 25). Die Mittelpunkte der Parkettsteine bilden ein regelm§iges Dreiecksraster.
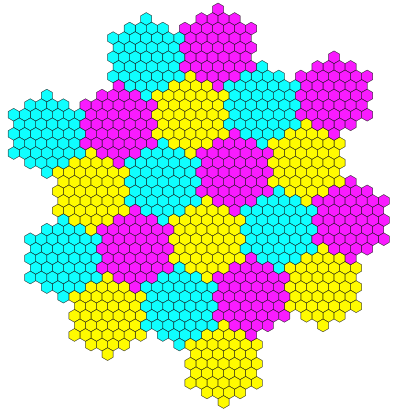
Abb. 25:Parketteriung
5 Wie geht es weiter?
Die Frage ist falsch gestellt. Es msste hei§en: Geht es weiter?
Wir knnen zwar problemlos zum Beispiel Pentanomialkoeffizienten bilden. Diese lassen sich auch in einem Quadratraster anordnen. Und die Hexanomialkoeffizienten lassen sich in einem Hexagonalraster anordnen. Allerdings werden bei den Koeffizientendreiecken die Winkel an der Spitze immer stumpfer, ein passendes regelm§iges Vieleck msste mehr Ecken haben. Das ist aber in der Rastergeometrie nicht mglich.