Hans Walser, [20170613]
Regulre Rhomboeder
1 Worum geht es?
Wir untersuchen konvexe Polyeder, welche von kongruenten Rhomben begrenzt sind. Zustzlich machen wir folgende Regularittsvoraussetzung: An einer Ecke sollen entweder ausschlie§lich spitze Winkel der Rhomben oder ausschlie§lich stumpfe Winkel der Rhomben zusammensto§en.
Bekannte Beispiele sind das Rhombendodekaeder und das Rhombentriakontaeder. Wir werden zeigen, dass es keine anderen gibt.
Der Wrfel ist ein Grenzfall, den ich auch zu den regulren Rhomboedern zhle.
Der Beweis ist etwas mhsam.
Genau die regulren Rhomboeder haben eine Kantenberhrkugel.
2 Terminologie
Bei einem konvexen Rhomboeder mit kongruenten Seitenrhomben knnen an einer Ecke ausschlie§lich spitze Rhombenwinkel ansto§en. Eine solche Ecke nennen wir eine spitze Ecke. In den Abbildungen sind die spitzen Ecken rot markiert. Stumpfe Ecken mit ausschlie§lich stumpfen Rhombenwinkel sind blau markiert. Ecken, an denen sowohl spitze wie stumpfe Rhombenwinkel ansto§en, nennen wir ãgemischtÒ und markieren sie schwarz.
In der Figur der Abbildung 1a haben wir zwei spitze Ecken. An den brigen Ecken sto§en jeweils ein spitzer und zwei stumpfe Rhombenwinkel an. Dies kann durch Einzeichnen der langen Rhombendiagonalen sichtbar gemacht werden.
In der Abbildung 1b haben wir zwei stumpfe Ecken. An den brigen Ecken sto§en jeweils zwei spitze und eine stumpfer Rhombenwinkel an.
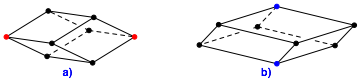
Abb. 1: Ecken
Ein regulres Rhomboeder soll jetzt also nur spitze (rote) und stumpfe (blaue) Ecken haben, keine gemischten.
3 Konvexitt
An jeder
Ecke mssen mindestens drei Rhomben ansto§en. Die Summe der Rhombenwinkel an
einer Ecke muss aber kleiner als 360¡ sein. Fr stumpfe Ecken hei§t das, dass
genau drei Rhomben ansto§en. Fr den stumpfen Rhombenwinkel ![]() gilt
daher:
gilt
daher:
![]() (1)
(1)
In einer stumpfen Ecke kommen immer genau drei Kanten zusammen. Stumpfe Ecken haben im grafentheoretischen Sinn den Grad 3.
Fr den
spitzen Rhombenwinkel ![]() gilt wegen
gilt wegen
![]() :
:
![]() (2)
(2)
Aus Konvexittsgrnden knnen an einer spitzen Ecke nicht mehr als fnf Rhomben ansto§en. Spitze Ecken knnen also die Grade 3, 4, oder 5 haben.
4 Regulre Rhomboeder
Fr die regulren Rhomboeder haben wir also bei spitzen Ecken die mglichen Grade 3, 4 oder 5. Es wird sich sogar zeigen, dass bei einem regulren Rhomboeder ausschlie§lich spitze Ecken desselben Grades vorkommen knnen. Eine Figur gem§ der Abbildung 2 mit zwei spitzen Ecken vom Grad 3 und drei spitzen Ecken vom Grad 4 ist also nicht mglich.
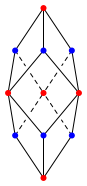
Abb. 2: Kein regulres Rhomboeder
Die Polyederformel von Euler hilft da nicht weiter.
4.1 Spitze Ecke vom Grad 3
Wir nehmen an, das Rhomboeder enthalte (mindestens) eine spitze Ecke vom Grad 3. Diese Ecke ist mit drei stumpfen Ecken verbunden, welche ebenfalls den Grad 3 haben (Abb. 3).
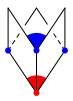
Abb. 3: Start mit einer spitzen Ecke vom Grad 3
Aus Parallelittsgrnden ist der blaue Winkel gleich dem roten Winkel (der rote Winkel ist ãhintenÒ). Andererseits mssen sich die beiden Winkel auf 180¡ ergnzen. Sie sind also rechte Winkel und wir sind in der Situation des Wrfels.
4.2 Spitze Ecke vom Grad 4
Wir beginnen mit der spitzen Ecke vom Grad 4 und bauen mit Rhomben auf gem§ Abbildung 4a.
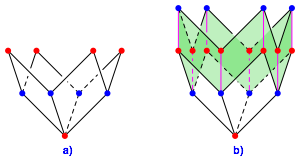
Abb. 4: Start mit einer spitzen Ecke vom Grad 4
Wenn wir jetzt eine noch nicht verwendete Kantenrichtung (magenta in Abb. 4b) einbauen, ergibt sich eine Zone von Rhomben (grn in Abb. 4b). Dies steht aber im Widerspruch dazu dass die stumpfen Ecken (blau) genau den Grad 3 haben.
Wir mssen also mit den bereits vorhandenen Kantenrichtungen weiterfahren. Damit ergibt sich eine Schlie§ungsfigur mit der Topologie des Rhombendodekaeders (Abb. 5a). Alle spitzen Ecken haben den Grad 4.
Zunchst haben wir allerdings erst ein allenfalls affin verzerrtes Bild des Rhombendodekaeders. Die Metrik braucht noch nicht zu stimmen. Da die Seitenrhomben aber kongruent sind, haben alle dieselbe lange Diagonale. In der Abbildung 5b sind diese Diagonalen rot eingezeichnet. Sie bilden die Kanten eines Oktaeders. Da alle Kanten gleich lang sind, ist das Oktaeder regulr. Die spitzen Ecken sind also die Ecken eines regulren Oktaeders.
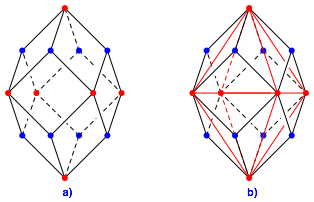
Abb. 5: Topologie des Rhombendodekaeders
Auf den Oktaederseiten sind kongruente dreiseitige Pyramiden mit den blauen Punkten als Spitzen aufgesetzt. Da die Pyramidenseiten benachbarter Pyramiden in einer Ebene liegen, haben wir es tatschlich mit dem Rhombendodekaeder zu tun.
Die
Diagonalen der Seitenrhomben haben das Verhltnis ![]() . Das entspricht dem Seitenverhltnis im DIN-Format
(Walser 2013b).
. Das entspricht dem Seitenverhltnis im DIN-Format
(Walser 2013b).
Der
spitze Winkel ![]() der
Seitenrhomben ist:
der
Seitenrhomben ist:
![]() (3)
(3)
4.3 Spitze Ecke vom Grad 5
Es kann weder eine spitze Ecke vom Grad 3 noch eine vom Grad 4 vorkommen. Daher haben alle spitzen Ecken den Grad 5.
Wir beginnen mit der spitzen Ecke vom Grad 5 und bauen mit Rhomben auf gem§ Abbildung 6a.
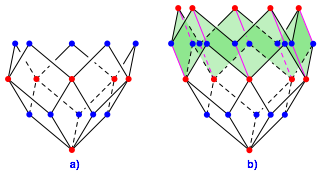
Abb. 6: Start mit einer spitzen Ecke vom Grad 5
Die roten Ecken in der obersten Lage von Abbildung 6a mssen aber den Grad 5 haben. Wir sind also gezwungen, eine zustzliche Kantenrichtung (magenta in Abb. 6b) einzufhren.
Die Figur der Abbildung 6b kann jetzt zu einer Schlie§ungsfigur mit der Topologie des Rhombentriakontaeders ergnzt werden (Abb. 7).
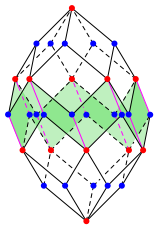
Abb. 7: Rhombentriakontaeder
Die langen Rhombendiagonalen bilden ein regulres Ikosaeder. Damit knnen wir schlie§en, dass wir es auch metrisch mit dem Rhombentriakontaeder zu tun haben.
Das
Diagonalenverhltnis der Seitenrhomben ist der Goldene Schnitt (Walser 2013a).
Der spitze Winkel ![]() der Seitenrhomben
ist:
der Seitenrhomben
ist:
![]() (4)
(4)
Damit ist bewiesen, dass Wrfel, Rhombendodekaeder und Rhombentriakontaeder die einzigen regulren Rhomboeder sind. Etwas viel Holz fr eine Geige.
5 Kantenberhrkugeln
Genau die regulren Rhomboeder haben eine Kantenberhrkugel, eine Kugel also, die alle Kanten berhrt.
Zunchst die Bilder.
5.1 Kantenmittenkugel beim Wrfel
Beim Wrfel berhrt die Kantenkugel in den Kantenmitten (Abb. 8a). Der Durchschnitt des Wrfels mit seiner Kantenmittenkugel ist der Spielwrfel mit abgerundeten Ecken (Abb. 8b).

Abb. 8: Kantenmittenkugel beim Wrfel
5.2 Kantenberhrkugel beim Rhombendodekaeder
Beim Rhombendodekaeder berhrt die Kantenberhrkugel nicht mehr in den Kantenmitten (Abb. 9a). Die Berhrpunkte dritteln die Kanten (nachrechnen).
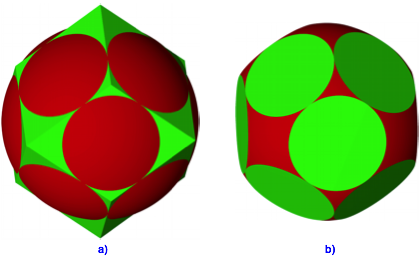
Abb. 9: Kantenberhrkugel beim Rhombendodekaeder
Die Abbildung 9b zeigt den zugehrigen Spielwrfel.
5.3 Kantenberhrkugel beim Rhombentriakontaeder
Die Abbildung 10 zeigt die Situation beim Rhombentriakontaeder.

Abb. 10: Kantenberhrkugel beim Rhombentriakontaeder
Die Berhrpunkte unterteilen die Kanten in einem Verhltnis, das dem Quadrat des Goldenen Schnittes entspricht.
5.4 Ausschluss weiterer Flle
Die Schnittfiguren der Kantenberhrkugel mit den Seitenrhomben sind deren Inkreise.
Bei Vorhandensein einer Kantenberhrkugel berhren sich die Inkreise benachbarter Seitenrhomben (Abb. 11a). Das geht nur, wenn jeweils spitze Winkel und stumpfe Winkel der Seitenrhomben benachbart sind, also im Fall regulrer Rhomboeder.

Abb. 11: Inkreise der Rhomben
Sobald gemischte Ecken auftreten (Abb. 11b) kann es keine Kantenberhrkugel geben.
Die regulren Rhomboeder lassen sich daher auch durch die Existenz einer Kantenberhrkugel charakterisieren.
Literatur
Walser, Hans (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.
Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.