Hans Walser, [20080103b]

Rekursiv definierte Parabeln

Anregung: Archimedes. [Netz/Noel 2007]

1 Worum es geht

Es werden rekursiv Punkte definiert, welche auf Parabeln liegen.

2 Unterteilen eines Intervalls

Wir unterteilen das Einheitsintervall fortlaufend durch Halbieren.

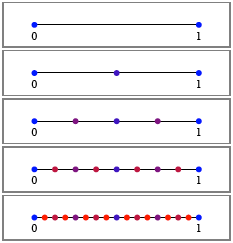
Fortlaufendes Unterteilen

Das kann mit den Startwerten und mit folgender Rekursion geschehen:

Dabei sind und das Ab- beziehungsweise Aufrundungssymbol. In MuPAD sieht das so aus:

x[0,0]:=0: x[0,1]:=1:

for i from 1 to n do

for k from 0 to 2^i do

x[i,k]:=1/2*(x[i-1,floor(k/2)]+x[i-1,ceil(k/2)]):

end_for:

end_for:

Für gerade k-Indizes ist und daher:

Für gilt folgende explizite Formel:

Dies ist eigentlich klar aus dem fortlaufenden Halbieren, kann aber auch induktiv aus der Rekursionsformel bewiesen werden:

(I) Für stimmt die explizite Formel mit den Startwerten überein.

(II) Induktionsvoraussetzung: . In die Rekursionsformel eingesetzt, ergibt dies

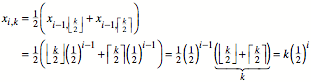
3 Rekursiv definierte y-Werte

In analoger Weise definieren wir nun y-Werte. Wir beginnen mit den Startwerten und und legen ein „Stichmaß“ fest. Auf die geometrische Bedeutung dieses „Stichmaßes“ kommen wir später zurück. Dann arbeiten wir mit der Rekursion:

Wir haben also gegenüber der Rekursion bei den x-Werten einen Zusatzterm

,

der jeweils nur bei den ungeraden k-Indizes eine Rolle spielt. Für gerade k-Indizes ist:

Der Zusatzterm enthält das Stichmaß s als Faktor und nimmt mit wachsendem i ab. In MuPAD:

y[0,0]:=0: y[0,1]:=1:

for i from 1 to n do

for k from 0 to 2^i do

y[i,k]:=1/2*(y[i-1,floor(k/2)]+y[i-1,ceil(k/2)])

+(k mod 2)*s*(1/4)^(i-1):

end_for:

end_for:

4 Die Parabel

Die folgende Figur lässt vermuten, dass die Punkte auf der grün eingezeichneten Parabel liegen, dass also gilt:

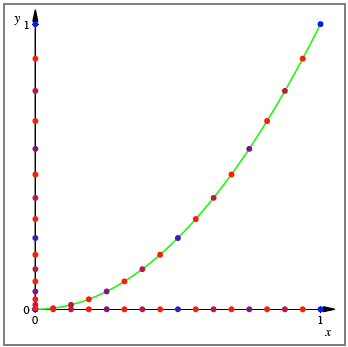
Parabel

Das kann induktiv bezüglich i bewiesen werden. Im Beweis arbeiten wir für mit der expliziten Formel .Wegen ist für :

(I) Für stimmt die Vermutung auf Grund der Startwerte.

(II) Induktionsvoraussetzung: .

Fallunterscheidung:

a) k gerade

In diesem Fall ist und:

b) k ungerade

Es ist und:

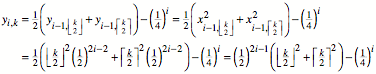
Nebenrechnung:

Somit ergibt sich:

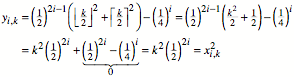
Damit ist die Vermutung bewiesen.

5 Das Stichmaß

Der Ausdruck kommt aus der Bauhütte. In unserem Kontext verstehen wir das Stichmaß gemäß Figur.

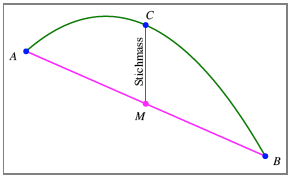
Stichmaß

Wir denken uns eine Sehne AB mit deren Mittelpunkt M. Senkrecht unter oder über M befindet sich der Kurvenpunkt C. Der Abstand von M nach C ist des Stichmaß. Dieses ist positiv, wenn C oberhalb von M liegt.

Das Stichmaß ist die größte senkrechte Abweichung der Kurve von der Sehne. Das Stichmaß ist eine Art Krümmungsparameter.

Für die Standardparabel mit und ist das Stichmaß .

6 Die a,b,c-Parabel

Für die Parabel in der „Schulform“ können wir mit den Startwerten und sowie dem Stichmaß arbeiten. Die folgende Figur illustriert den Fall .

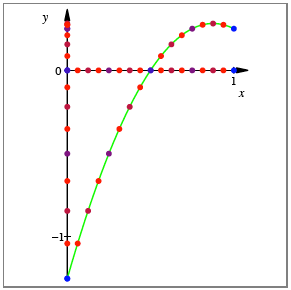
Parabel

7 Zwei Parabelpunkte und Stichmaß

Für die Parabelpunkte und sowie das Stichmaß s können wir mit den Startwerten und sowie und arbeiten. Die folgende Figur illustriert den Fall , und .

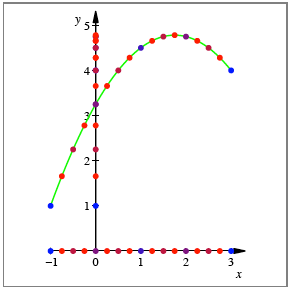
Zwei Parabelpunkte und Stichmaß

8 Stichmaß und Fläche

Wir zeichnen in den Parabelbogen das durch die beiden Endpunkte und das Stichmaß definierte Dreieck ein.

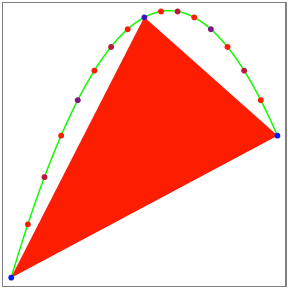
Dreieck

Der Flächeninhalt dieses Dreieckes ist gegeben durch die horizontale Ausdehnung sowie das Stichmaß s, nämlich:

Nun zeichnen wir zwei weitere Dreiecke und ein:

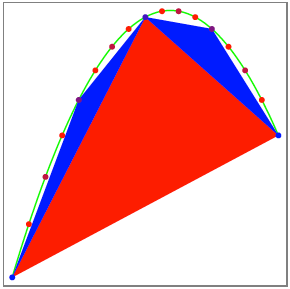
Zwei weitere Dreiecke

Die größte Ausdehnung dieser beiden Dreiecke in der senkrechten Richtung ist noch ein Viertel des Stichmaßes. Dies geht aus der Rekursionsformel für hervor. Die gesamte horizontale Ausdehnung ändert sich nicht. Die Gesamtfläche dieser beiden Dreiecke ist also:

Wir haben für diese beiden Dreiecke gesamthaft nur noch einen Viertel der Fläche des ersten Dreieckes.

Im nächsten Schritt erhalten wir vier zusätzliche Dreiecke.

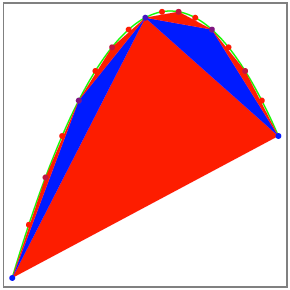
Vier zusätzliche Dreiecke

Sie haben gesamthaft den Flächeninhalt:

In der folgenden Figur sind noch einige weitere Generationen von Dreiecken eingezeichnet. Wir sehen, dass die Dreiecke das Parabelsegment von innen ausschöpfen. Die eigentlich „eckige“ Randlinie ist von einer glatten Kurve optisch nicht unterscheidbar.

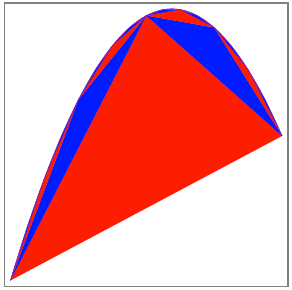
Ausschöpfung des Parabelsegmentes

Die Flächen aller dieser Dreiecke bilden insgesamt eine geometrische Reihe:

Die von innen ausgeschöpfte Fläche des Parabelsegmentes misst also vier Drittel der Fläche des ersten Dreieckes.

9 Kubische Parabel

Durch eine leichte Modifikation (rot) der Rekursionsformel für erhalten wir die kubische Standardparabel:

Der Faktor k im Zusatzterm macht diesen asymmetrisch und unsympathisch. Er verunmöglicht eine einfache Flächenberechnung nach obigem Muster.

Das folgende Bild bezieht sich auf Die Startwerte und sowie und und das „Stichmaß“ .

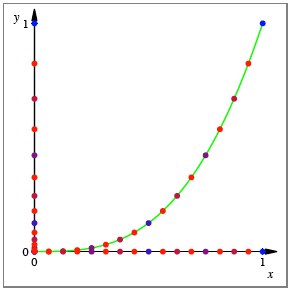
Kubische Parabel

Rekursiv kann gezeigt werden, dass in dieser Situation gilt: .

Literatur

[Netz/Noel 2007] Netz, Reviel und Noel, William: Der Kodex des Archimedes. Das berühmteste Palimpsest der Welt wird entschlüsselt. Aus dem Englischen von Thomas Filk. 2. Auflage. München: Verlag C. H. Beck 2007. ISBN 978 3 406 56336 2