Hans Walser, [20161219]
Reuleaux-Dreieck
1 Worum geht es?
Es wird die elliptische Bewegung eines Reuleaux-Dreieckes in einem Quadrat illustriert.
2 Gleichdick
Das Reuleaux-Dreieck ist in jeder Richtung gleich dick. Es kann daher in beliebiger Position so in einen gleich dicken Streifen eingelegt werden, dass in jeder Position Ober- und Unterkante des Streifens berźhrt werden (Abb. 1).
Insbesondere kann es auch in die Schnittfigur zweier gleich breiter Streifen (Rhombus) berźhrend eingelegt werden. Wir untersuchen den Sonderfall des Quadrates.
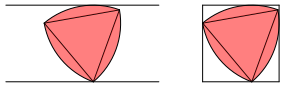
Abb. 1: Reuleaux-Dreieck in Streifen und Quadrat
Die GeoGebra-Animation A1 illustriert die Bewegung im Quadrat.
3 Elliptische Bewegung
3.1 Keine Drehung
Das Reuleaux-Dreieck dreht sich zwar im Quadrat, die Bewegung ist aber keine Drehung um einen festen Drehpunkt. Dies ist schon deshalb ausgeschlossen, weil sich die Ecken zeitweise auf den geraden Quadratseiten bewegen.
3.2 Ellipsenzirkel
Die beiden Endpunkte eines Stabes fester LŠnge sollen auf je einer von zwei gekreuzten Schienen verlaufen (Abb. 2). Dann beschreibt jeder beliebige Punkt auf dem Stab eine Ellipse. Die beiden Abschnitte des Stabes ergeben die LŠngen der langen und der kurzen Halbachse. Mit GerŠten dieser Art hat man frźher Ellipsen gezeichnet.
Der Mittelpunkt des Stabes beschreibt einen Kreis. Die beiden Endpunkte des Stabes beschreiben je eine Strecke. Beides sind SonderfŠlle von Ellipsen.
Auch die Punkte in den VerlŠngerungen des Stabes beschreiben Ellipsen.
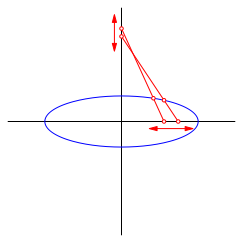
Abb. 2: Ellipsenzirkel
Mehr noch: Wir kšnnen an den Stab eine Ebene heften, die mitbewegt wird. Jeder Punkt dieser Ebene beschreibt eine Ellipse in der Grundebene, in welcher die Kreuzschienen liegen.
Die Schienen mźssen sich nicht orthogonal kreuzen. Es gibt auch bei schiefen Kreuzschienen Ellipsen.
3.3 Anwendung in unserem Beispiel
In jeder Position des Reuleaux-Dreiecks im Quadrat berźhren (mindestens) zwei der drei Ecken je eine Quadratseite, welche orthogonal zueinander stehen(Abb. 3).
Daher funktioniert die Angelegenheit wie ein Ellipsenzirkel. Jeder Punkt des Reuleaux-Dreiecks beschreibt eine Ellipse, wenigsten so lange, als beide Eckpunkt ihre Quadratseite berźhren.
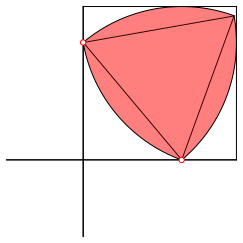
Abb. 3: Ellipsenzirkel im Quadrat
Nun hat aber das Quadrat vier rechte Winkel und damit vier Kanten, die als Kreuzschienen fungieren kšnnen. Au§erdem sind es im Wechsel immer zwei andere der drei Ecken des Reuleaux-Dreieckes, welche auf einer Quadratseite sich bewegen. Daher ist die Bahnkurve eines Punktes des Reuleaux-Dreiecks aus vier Ellipsenbšgen zusammengesetzt. Wir haben also eine Zusammensetzung von vier elliptischen Bewegungen.
Die GeoGebra-Animation A1 ist daher aus vier konsekutiven Animationen zusammengesetzt, von denen immer nur eine aktiv ist. Drei sind inaktiv, daher die vielen ăundefiniertŇ-Notationen im algebraischen Begleittext. Technisch wird das mit Fallunterscheidungen fźr den Parameter t gehandhabt.
Da die Kreuzschienen auch schief zueinander stehen dźrfen, gilt entsprechendes fźr ein Reuleaux-Dreieck, das sich in einem Rhombus bewegt.
3.4 Bahnkurve des Mittelpunktes
In der GeoGebra-Animation A1 ist blau der Mittelpunkt des Reuleaux-Dreieckes eingezeichnet. Optisch sieht es so aus, als wźrde er sich auf einem Kreislein bewegen. In Wirklichkeit ist seine Bahnkurve ebenfalls aus vier Ellipsenbšgen zusammengesetzt.
Die Abbildung 4 zeigt die vier Ellipsen. Der Mittelpunkt des Reuleaux-Dreiecks bewegt sich auf den innersten kleinen Ellipsenbšgen.
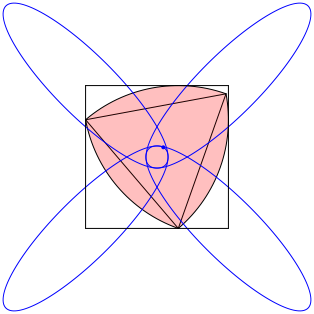
Abb. 4: Die vier Ellipsen
Die
Ellipsen haben ihre Zentren in den Quadratecken. Die Achsen sind parallel zu
den Quadratdiagonalen. In einem Quadrat der SeitenlŠnge 1 haben die Ellipsen
eine lange Halbachse ![]() und eine
kurze Halbachse
und eine
kurze Halbachse ![]() . Die beiden Halbachsen ergŠnzen sich auf 1.
. Die beiden Halbachsen ergŠnzen sich auf 1.
Die GeoGebra-Animation A2 zeigt die Bewegung des Mittelpunktes auf den Bahnellipsen. Das Reuleaux-Dreieck dreht sich im positiven Drehsinn, sein Mittelpunkt kurvt aber im negativen Drehsinn.