Hans Walser, [20120513]

Reuleaux-Dreieck, Tetraeder und Seifenblasen

Das Reuleaux-Dreieck kann durch geeignete Projektionen aus dem Tetraeder hergeleitet werden.

1 Das Reuleaux-Dreieck

Die Abbildung 1 zeigt das Reuleaux-Dreieck.

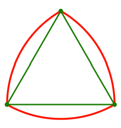
Abb. 1: Reuleaux-Dreieck

Es besteht aus drei Kreisbögen, deren Zentren die Ecken eines gleichseitigen Dreiecks sind. Das Reuleaux-Dreieck hat überall denselben Durchmesser, ist also ein so genanntes Gleichdick.

An den Ecken hat das Reuleaux-Dreieck Innenwinkel von 120°.

2 Tetraeder

Wir beginnen mit einem regelmäßigen Tetraeder und zeichnen seine Umkugel (Abb. 2). Eine Tetraederecke, die Spitze, kommt in den Nordpol zu liegen. Die drei übrigen Tetraederecken liegen auf den Meridianen 0°, 120°E, 120°W. Sie haben alle die Breite:

Das Bodendreieck des Tetraeders liegt also südlich der Äquatorebene.

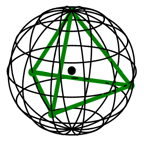
Abb. 2: Tetraeder mit Umkugel

Nun projizieren wir die Kanten des Tetraeders auf die Umkugel. Dadurch entstehen vier regelmäßige sphärische Dreiecke (Abb. 3).

Drei der sechs Großkreisbögen gehen vom Nordpol aus, liegen also auf Meridianen.

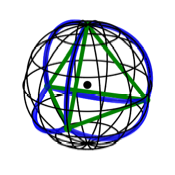
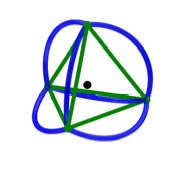
Abb. 3: Sphärische Dreiecke

Diese regelmäßigen sphärischen Dreiecke sind aus Großkreisbögen zusammengesetzt und haben Innenwinkel von 120°, da an jeder Ecke drei solche Dreiecke zusammenstoßen.

Die sphärischen Dreiecke sind also gleich aufgebaut wie das Reuleaux-Dreieck. Wie bringen wir diese sphärischen Dreiecke in die Ebene?

3 Stereografische Projektion

Die stereografische Projektion ist eine konforme, das heißt winkeltreue, Abbildung von der Kugel in die Ebene. Sie ist eine Zentralprojektion von einem Kugelpunkt aus auf eine Ebene, welche normal zur Geraden durch das Projektionszentrum und das Kugelzentrum geht.

Die stereografische Projektion ist auch kreistreu, genau genommen Möbius-Kreis-treu. Kreise auf der Kugel werden im Regelfall auf Kreise abgebildet. Wenn allerdings der Kreis durch das Projektionszentrum geht, ist sein Bild eine Gerade. Möbius (August Ferdinand Möbius, 1790-1868, Erfinder des Möbius-Bandes) fasste daher die Kreise und Geraden der Ebene unter einem Oberbegriff zusammen. Dieser Oberbegriff wird heute als Möbius-Kreis bezeichnet.

Unsere sphärischen Dreiecke werden also bei einer stereografischen Projektion auf Dreiecke mit Innenwinkeln von 120° abgebildet, deren Seiten Möbius-Kreise sind. Wir haben also eine Chance, dass dabei unser Reuleaux-Dreieck entsteht. Das ist letztlich die Frage der Wahl eines geeigneten Projektionszentrums.

4 Projektion vom Nordpol aus

Wir projizieren vom Nordpol aus auf die Äquatorebene (Abb. 4).

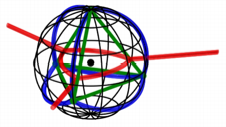
Abb. 4: Projektion vom Nordpol aus

Die Abbildung 5 zeigt die Situation im Grundriss. Die Bilder der drei vom Nordpol, also dem Projektionszentrum, ausgehenden Großkreisbögen, sind Halbgeraden, die sich bis ins Unendliche erstrecken.

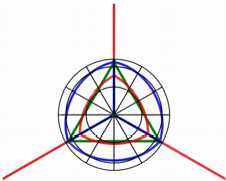
Abb. 5: Grundriss

In der Abbildung 6 ist nur noch das stereografische Bild eingezeichnet. Wir erkennen im Zentrum ein Reuleaux-Dreieck.

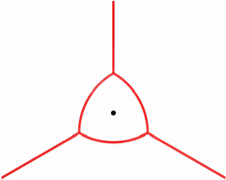
Abb. 6: Reuleaux-Dreieck im Zentrum

5 Projektion vom Südpol aus

Wir projizieren nun vom Südpol aus auf die Äquatorebene (Abb. 7)

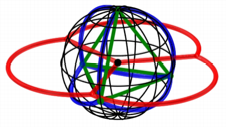
Abb. 7: Projektion vom Südpol aus

Die Abbildung 8 zeigt die Situation im Grundriss.

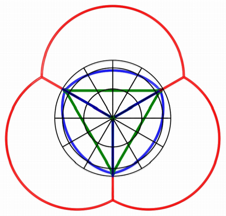
Abb. 8: Grundriss

In der Abbildung 9 ist nur noch das stereografische Bild eingezeichnet.

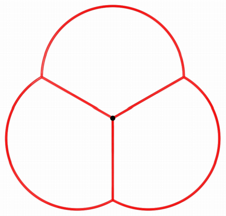
Abb. 9: Wer sieht das Reuleaux-Dreieck?

Die Abbildung 10 zeigt, wie die Rosette mit dem Reuleaux-Dreieck in Beziehung gebracht werden kann.

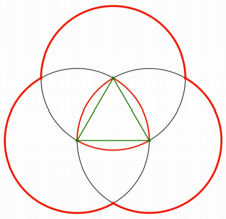
Abb. 10: Rosette und Reuleaux-Dreieck

6 Projektion vom Ostpunkt aus

Wir projizieren vom Punkt mit den geografischen Koordinaten aus auf die Ebene durch den 0°-Meridian (Abb. 11).

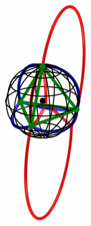
Abb. 11: Projektion vom Ostpunkt aus

In der Abbildung 12 sehen wir die Situation im Seitenriss.

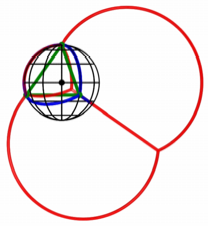
Abb. 12: Im Seitenriss

In der Abbildung 13 schließlich ist nur noch das stereografische Bild eingezeichnet. Hier ist kein Reuleaux-Dreieck mehr erkennbar. Die Figur erinnert an Seifenblasen.

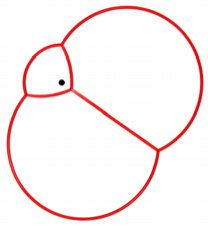
Abb. 13: Seifenblasen