Hans Walser, [20121112]

Spiel mit Reuleaux-Dreiecken

Einem regelmäßigen Sechseck passen wir zwei um 60° verdrehte Reuleaux-Dreiecke ein (Abb. 1).

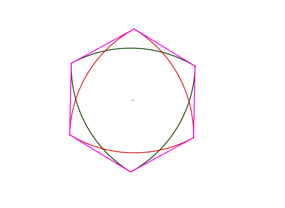
Abb. 1: Reuleaux-Dreiecke

Nun suchen wir die Punkte, welche von den beiden Reuleaux-Dreiecken gleichen Abstand haben („ausmitteln“). Das sind die Zentren der Kreise, welche beide Reuleaux-Dreiecke berühren (Abb. 2).

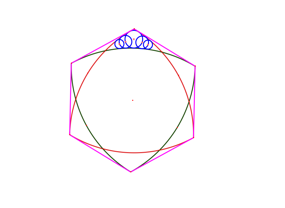
Abb. 2: Punkte gleichen Abstandes

Diese Punkte liegen auf Ellipsen, welche zwei aufeinanderfolgende Ecken des Sechsecks als Brennpunkte haben (Abb. 3). Die Ellipsen sind fast Kreise, das Verhältnis der langen Achse zur kurzen Achse ist 1.0444659357.

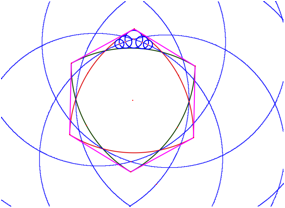
Abb. 3: Ellipsen

Der Durchschnitt dieser Ellipsen ist kein Gleichdick (Abb. 4).

Abb. 4: Kein Gleichdick

Eine Figur mit der Symmetrie des regelmäßigen Sechsecks (allgemein des regelmäßigen 2n-Ecks) kann kein Gleichdick sein.

Der Faktor zwischen dem längsten und dem kürzesten Durchmesser ist in unserem Beispiel 1.0798321007.