Hans Walser, [20130608a], Version 14. Juni 2013

Reuleaux-Dreieck-Triangulation

Anregung: R. V., S.

1 Problemstellung

Gesucht ist eine „schöne“ Triangulation des Reuleaux-Dreiecks (Abb. 1).

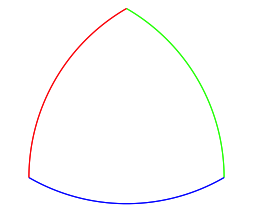
Abb. 1: Reuleaux-Dreieck

2 Idee

Wir zeichnen eine lineare Triangulation auf den Boden eines Tetraeders, projizieren vom Zentrum aus auf seine Umkugel (inverse gnomonische Projektion) und dann vom Nordpol aus auf eine Tangentialebene im Südpol (stereografische Projektion).

3 Schritt für Schritt

3.1 Lineare Triangulation und Tetraeder

Die Abbildung 2 zeigt eine lineare Triangulation in einem gleichseitigen Dreieck. Sie hat eine Zehner-Teilung: Jede Dreiecksseite ist in zehn Teile unterteilt. Insgesamt haben wir daher 100 Teildreiecke.

Abb. 2: Lineare Triangulation

Diese lineare Triangulation setzen wir nun auf den Boden eines regulären Tetraeders (Abb. 3).

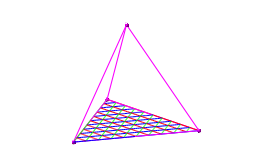
Abb. 3: Tetraeder

3.2 Die Kugel kommt ins Spiel

Wir zeichnen und denken uns die Umkugel des Tetraeders (Abb. 4). Die Spitze des Tetraeders liegt in Nordpol, die drei Basispunkte sind auf dem Breitenkreis 19.47°S.

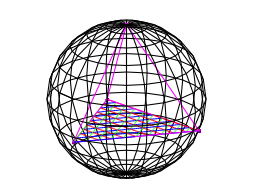
Abb. 4: Umkugel des Tetraeders

Nun projizieren wir die lineare Triangulation auf dem Tetraederboden vom Kugelmittelpunkt aus auf die Kugeloberfläche (Abb. 5). Auf der Kugeloberfläche besteht die Triangulation aus Großkreisbögen.

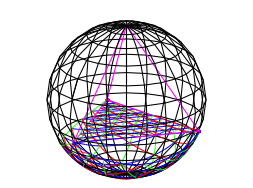
Abb. 5: Projektion vom Kugelmittelpunkt aus

Da dies recht unübersichtlich ist, lassen wir die Kugel mal weg (Abb. 6).

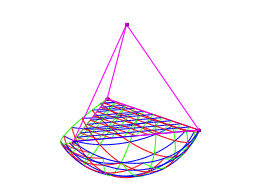
Abb. 6: Ohne Bild der Kugel

Wir können auch noch die lineare Triangulation auf dem Tetraederboden weglassen (Abb. 7).

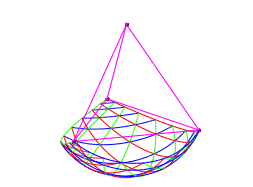
Abb. 7: Fischernetz am Tetraeder

Die Abbildung 8 zeigt dasselbe von der Seite.

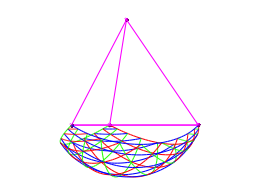
Abb. 8: Spezielle Sicht

3.3 Projektion auf die Tangentialebene am Südpol

Wir projizieren nun vom Nordpol (das ist die Tetraederspitze) aus auf die Tangentialebene am Südpol. Diese Abbildung heißt stereografische Projektion. Sie ist winkeltreu (konform) und wird daher in der Kartografie gerne verwendet. Die Abbildung 9 zeigt das Vollbild.

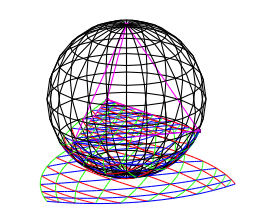
Abb. 9: Stereografische Projektion

Die Abbildung 10 zeigt die Situation von der Seite.

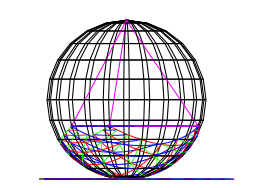
Abb. 10: Sicht von der Seite

Die Abbildung 11 zeigt das Vollbild aus der Sicht von „unten“. Wir sehen auf den Südpol.

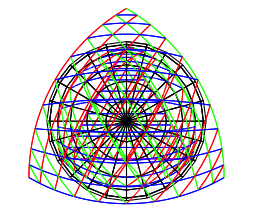
Abb. 11: Sicht auf den Südpol

Nun lassen wir die ganze Herleitung weg und sehen die gesuchte Triangulation (Abb. 12). Die Krümmungen der Triangulationslinien suggerieren eine Wölbung. In der Mitte haben wir einen Lupeneffekt.

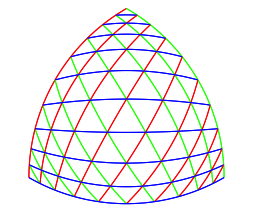
Abb. 12: Triangulation des Reuleaux-Dreieckes

3.4 Hintergrund

Die Projektion des regulären Tetraeders auf eine konzentrische Sphäre unterteilt diese in vier kongruente regelmäßige sphärische Dreiecke mit Winkeln von 120°.

Die stereografische Projektion ist winkeltreu und Möbiuskreis-treu. Wir erhalten daher in der Projektion genau das Reuleaux Dreieck.

3.5 Krümmungsverhalten

Die zum Beispiel roten Kreise der Abbildung 12 sind unterschiedlich gekrümmt. Somit muss es einen „Durchgang durch null“ ergeben. Krümmung null bedeutet aber eine Gerade. Dies wird sichtbar bei einer Teilungszahl, welche durch drei teilbar ist. Die Abbildung 13 zeigt die Situation mit einer Zwölfer-Teilung. Wir haben drei Geraden durch die Mitte.

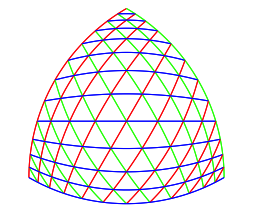
Abb. 13: Geraden durch die Mitte

4 Händische Konstruktion mit Zirkel und Lineal

Wir untersuchen nun, wie die Triangulation des Reuleaux-Dreieckes rein elementar mit Zirkel und Lineal bewerkstelligt werden kann.

Für die praktische Durchführung arbeiten wir im Folgenden mit der Teilungszahl fünf. Die Abbildung 14 zeigt die Triangulation des Reuleaux-Dreieckes mit der Teilungszahl fünf.

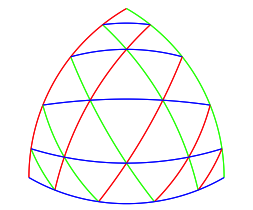
Abb. 14: Teilungszahl 5

4.1 Herleitung

Die Abbildung 15 zeigt zunächst nochmals das räumliche Vollbild mit der Teilungszahl fünf, aber aus einer sehr speziellen Sicht.

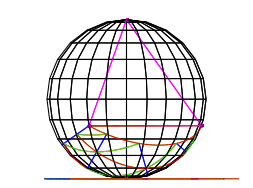
Abb. 15: Sehr spezielle Sicht

Wir gucken in Richtung einer Bodenkante des Tetraeders. In dieser Sicht erscheinen die blauen Großkreisbogen auf der Kugel als Strecken (Abb. 16).

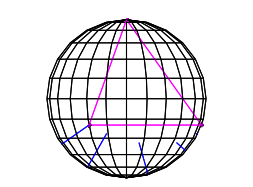
Abb. 16: Blaue Großkreise erscheinen als Geraden

Mehr noch: Wenn wir diese Strecken verlängern, schneiden sich alle in einem Punkt (Abb. 17).

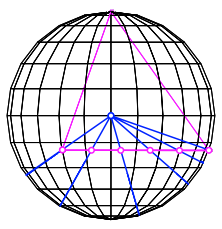
Abb. 17: Schnittpunkt

Die scheinbaren blauen Geraden sind in Wirklichkeit Großkreisbögen auf der Kugel, nach der Verlängerung sogar halbe Großkreise, die in zwei diametralen Punkten auf dem Äquator enden. In unserer Sicht können die Winkel zwischen den Halbkreisen direkt abgelesen werden.

Weiter unterteilen die blauen Strecken die magenta Bodenlinie des Tetraeders in fünf gleiche Teile. Genau genommen: es wird die Höhe des Bodendreieckes in fünf gleiche Teile geteilt. Unsere gewählte Teilungszahl fünf wird also sichtbar.

4.2 Das DIN-Format erscheint

Schließlich – und das ist verblüffend – passen zwischen Tetraederboden und Äquator genau drei Rechtecke mit dem Seitenverhältnis des DIN-Formates hinein (Abb. 18). Dies ist unabhängig von unserer Teilungszahl fünf.

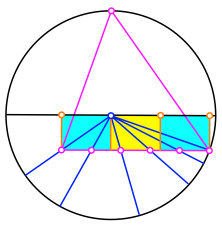
Abb. 18: Das DIN-Format erscheint

Wenn wir nun noch bedenken, dass die stereografische Projektion, welche ja schließlich die Triangulation geliefert hat, winkel- und kreistreu ist, wird folgende Konstruktion plausibel. Der Nachweis der Korrektheit ist etwas aufwändig.

4.3 Konstruktion

Wir beginnen mit drei im Querformat aneinandergefügten DIN-Rechtecken gemäß Abbildung 19 und unterteilen die obere Gesamtseite gemäß der gewählten Teilungszahl, in unserem Beispiel also in fünf Teile. Wir haben eine so genannte reguläre Skala.

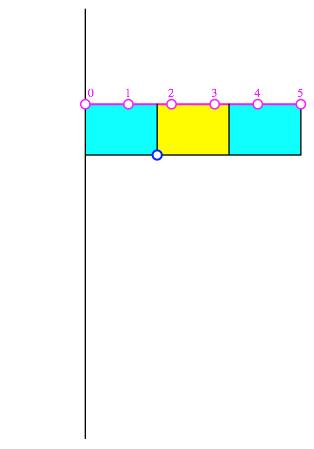
Abb. 19: Drei DIN-Rechtecke. Reguläre Skala

Nun projizieren wir die reguläre Skala über den in der Abbildung 19 eingezeichneten blauen Punkt auf die linke senkrechte Gerade (Abb. 20). Wir erhalten eine so genannte projektive Skala. Sie ist nicht mehr äquidistant, auch die Reihenfolge der Zahlen ist nicht die übliche. Die Sache hat noch eine Tücke. Wenn wir mit einer durch drei teilbaren Teilungszahl arbeiten, ergibt sich ein magenta Punkt auf der regulären Skala, der in der projektiven Skala nicht erscheint. Bei der Teilungszahl zwölf ist es der Punkt mit der Nummer vier. Dies ist ein so genannter Verschwindungspunkt. Es ist ein „unendlich ferner“ Punkt.

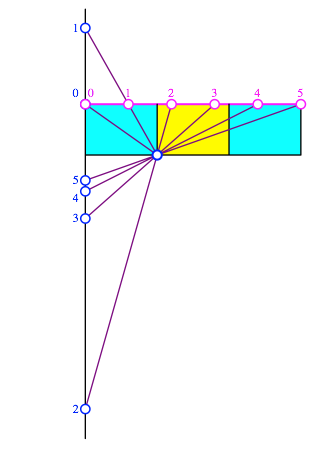
Abb. 20: Projektive Skala

Die Punkte der projektiven Skala verwenden wir nun als Zentren von Kreisbögen gemäß Abbildung 21. Falls wir einen unendlich fernen Punkt als Zentrum im Spiel haben, wird der zugehörige Kreisbogen zur horizontalen Strecke.

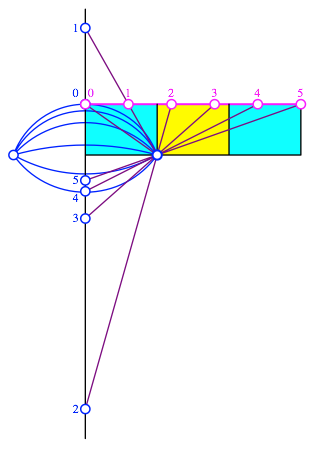
Abb. 21: Kreisbögen

Wir kopieren diese Kreisbögen zwei Mal, färben um, drehen um 120° beziehungsweise 240° und überlagern (Abb. 22).

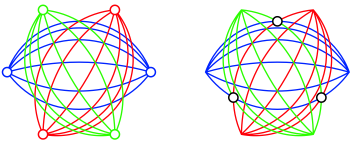
Abb. 22: Triangulation

Zwischen den schwarz markierten Punkten erkennen wir das triangulierte Reuleaux-Dreieck der Abbildung 14.

4.4 Ausweitung

Wir können die in der Abbildung 19 eingeführte reguläre Skala links über 0 in die negativen Zahlen und rechts über fünf hinaus vergrößern. Das führt dann zu einer Triangulation der Kreisscheibe (Abb. 23). Wo ist unser ursprüngliches Reuleaux-Dreieck?

Abb. 23: Triangulation des Kreises. Teilungszahl 5

Die Abbildung 24 zeigt das Beispiel mit der durch drei teilbaren Teilungszahl zwölf. Es gehen drei Durchmesser durch das Kreiszentrum.

Abb. 24: Teilungszahl 12