Hans Walser, [20210224]
Rhomben-Pythagoras
1 Worum geht es?
Spiel mit Šhnlichen Rhomben.
2 Vorgehen
Zwischen die Ecken eines rechtwinkligen Dreiecks (Abb. 1a) spannen wir ăschlankeŇ Šhnliche Rhomben ein (Abb. 1b). Im Beispiel der Abbildung 1 wurde das so gemacht, dass die langen Rhombendiagonalen die ehemaligen Dreiecksseiten sind. Wenn die Rhomben zu ŇdickŇ sind, źberschneiden sie sich und die Gesamtfigur wird unansehnlich. Dasselbe gilt erst recht, wenn wir entsprechend mit den kurzen Rhombendiagonalen arbeiten.
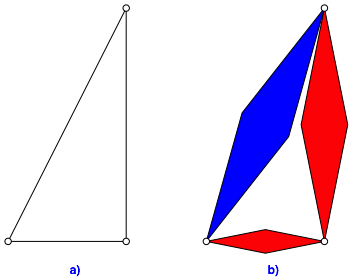
Abb. 1: Vorgehen
Nun gilt folgender FlŠchensatz: Die FlŠchensumme der beiden Kathetenrhomben ist gleich dem FlŠcheninhalt des Hypotenusenrhombus. Dies kann mit verschiedenen Argumenten aus dem Satz des Pythagoras hergeleitet werden.
3 Zerlegungsgleichheit
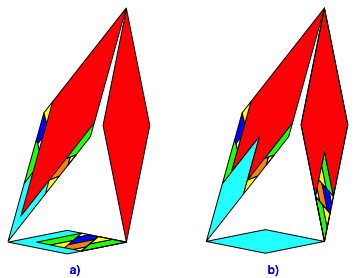
Abb. 2: Zerlegungsgleichheit
Die Abbildung 2 zeigt je eine gemeinsame Zerlegung der beteiligten Rhomben.
Websites
Hans Walser: Pythagoras-Zerlegungsbeweise