Hans Walser, [20130326]
Rhomben
Anregung: R. S., C.
1 Konstruktionsvorgang
Wir beginnen mit 
Punkten 
mit 
. Die Abbildung 1 zeigt die Situation fŸr 
.
Abb. 1: Ausgangslage
Nun ergŠnzen wir die Punkte zu Rhomben mit der SeitenlŠnge 1 gemŠ§ Abbildung 2. Zwei aufeinander folgende Punkte werden diametrale Eckpunkte eines Rhombus.
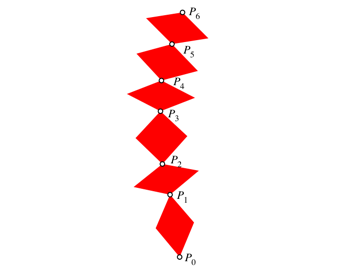
Abb. 2: Rhomben der SeitenlŠnge 1
Wir ergŠnzen mit weiteren Rhomben gemŠ§ Abbildung 3.
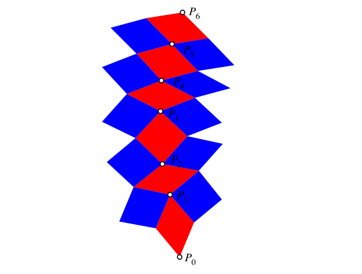
Abb. 3: Weitere Rhomben
Schlie§lich kšnnen wir weitere Rhomben anfŸgen gemŠ§ Abbildung 4. Es entsteht ein dynamisches Schachbrettmuster.
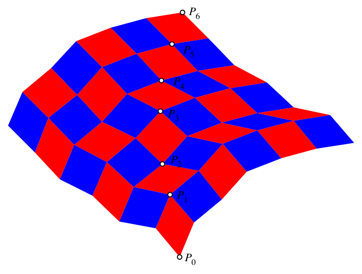
Abb. 4: ErgŠnzung zum dynamischen Schachbrettmuster
Das dynamische
Schachbrettmuster ist nur abhŠngig von den 
Punkten 
.
Die Figur kann zu einer Kachelung der ganzen Ebene ausgeweitet werden (Abb. 5). Das liegt daran, dass gegenŸberliegende Seiten kongruent und parallel sind. Die Šu§ersten Ecken bilden ein Parallelogramm (in der Regel kein Rhombus).
Abb. 5: Kachelung der Ebene
2 Spezielle Lage der Basispunkte. Beispiele
2.1 V-Form
In der Abbildung 6 sind
die Basispunkte V-fšrmig und mit dem Abstand 
angeordnet. Wir
erhalten ein Karo-Raster, das um die Ecke geht.
Abb. 6: Karo-Raster um die Ecke
Die Abbildung 7 zeigt die zugehšrige Kachelung der Ebene.
Abb. 7: Tanzende Quadrate
2.2 Punkte auf Parabel
Die Basispunkte sind bezŸglich der x-Koordinate gleichmŠ§ig und symmetrisch auf einer quadratischen Parabel verteilt (Abb. 8).
Abb. 8 Punkte auf Parabel
Die Abbildung 9 zeigt die zugehšrige Kachelung der Ebene.
Abb. 9: Kachelung der Ebene
2.3 Der Zickzack im Winkel
Wir wŠhlen einen
Winkel, der einen Bruchteil von 180¡ misst. In der Abbildung 10 ist ein Winkel
von 15¡ gewŠhlt worden. Auf dem einen Schenkel wŠhlen wir einen beliebigen
Punkt 
und ergŠnzen zu
einer Zickzacklinie der SeitenlŠnge 1 gemŠ§ Abbildung 10. †ber Zickzack-Linien
dieser Art siehe [Francke 2011a], [Francke 2011b] und [Walser 1988].
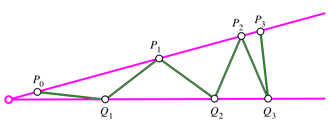
Abb. 10: Winkel und Zickzacklinie
Nun passen wir die Rhomben ein (Abb. 11).
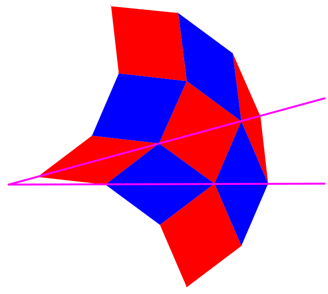
Abb. 11: Einpassen der Rhomben
Die Figur ist achsensymmetrisch. Wegen der speziellen Wahl des Winkels kann sie zu einer Rosette ergŠnzt werden (Abb. 12). In der Mitte haben wir allerdings ein Loch.
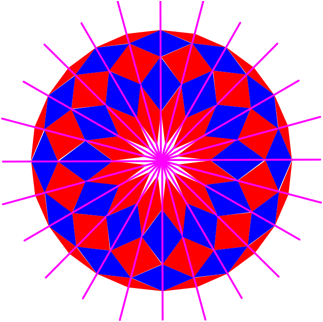
Abb. 12: Rosette
Wir legen nun den Punkt
speziell in den
Scheitelpunkt (Abb. 13).
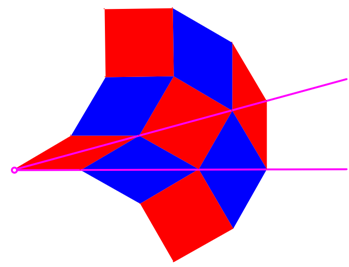
Abb. 13: Startpunkt im Scheitel
SŠmtliche Rhombenwinkel sind nun in einem rationalen VerhŠltnis zu 360¡. Ausspiegeln ergibt die Rose der Abbildung 14. In der Mitte haben wir kein Loch mehr.
Abb. 14: Rose
Der Umriss der Rose ist ein regelmŠ§iges Vieleck, in der Abbildung 14 ein regelmŠ§iges Zwšlfeck.
Allerdings lŠsst sich das regelmŠ§ige Vieleck sparsamer mit den Rhomben auskacheln (Abb. 15).
Abb. 15: Tulpe
Literatur
[Francke 2011a] Francke Dietrich: Gleichschenklige Teildreiecke im regelmŠ§igen Vieleck. Elemente der Mathematik 66 (2011), S. 155-163.
[Francke 2011b] Francke, Dietrich: Vielfachteilung eines Winkels mittels Halbierungsrhomben. Die Wurzel, 45, Juni 2011, S. 135-137.
[Walser 1988] Walser, Hans: Ein Schlie§ungssatz der Elementargeometrie. Elemente der Mathematik (43), 1988, 161-169.