Hans Walser, [20210207], [20240418]
Rhomben
1 Worum geht es?
Eine Schließungsfigur mit ähnlichen Rhomben
2 Schritt für Schritt
Wir zeichnen zwei ähnliche rote Rhomben, welche eine spitze Ecke in U (U ist der Nullpunkt des x-y-Koordinatensystems) gemeinsam haben. Die Ähnlichkeit der Rhomben legen wir durch das Diagonalenverhältnis v (kurze Diagonale zu lange Diagonale) fest.
Die Abbildung 1 zeigt die Situation für v = ½.
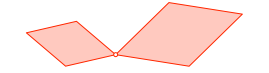
Abb. 1: Zwei ähnliche Rhomben
Nun passen wir zwischen die stumpfen Ecken der roten Rhomben zwei weitere Rhomben (blau) ein, welche ähnlich sind zu den roten (Abb. 2).
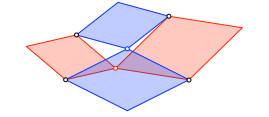
Abb. 2: Zwei weitere Rhomben
Die beiden neu eingefügten Rhomben haben eine Ecke gemeinsam. Wir haben eine Schließungsfigur. Die Schließungsfigur ist struktursymmetrisch.
Natürlich könnten wir auch zwei stumpfe Ecken in U legen und entsprechend dual weiterfahren.
3 Beweis
Der Beweis ist eine idyllische Rechenaffäre. Für den Start verwenden wir die Bezeichnungen der Abbildung 3.
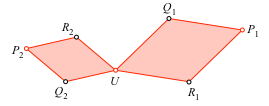
Abb. 3: Bezeichnungen
Die Situation der beiden Rhomben ist durch v sowie P1 und P2 gegeben. Wir setzen:
![]()
Damit lassen sich die Koordinaten der Punkte Q1 und Q2 sowie R1 und R2 berechnen:
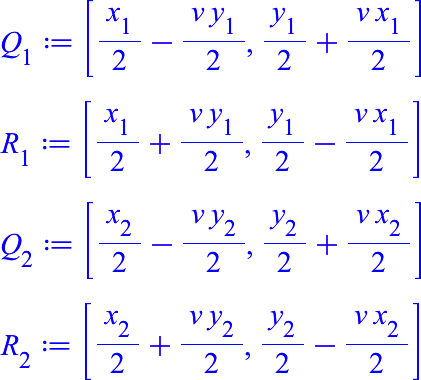
Nun setzen wir oben einen blauen Rhombus ein (Abb. 4).
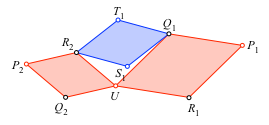
Abb. 4: Eingesetzter Rhombus
Für die freien Ecken erhalten wir:
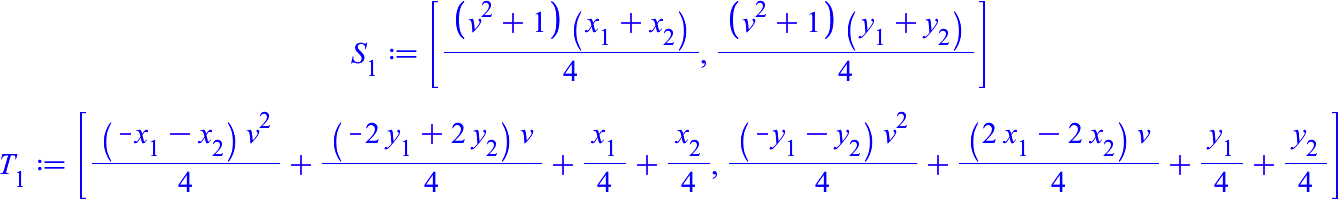
Wir hätten ebenso gut den unteren Rhombus einsetzen können (Abb. 5).
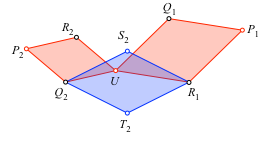
Abb. 5: Unterer Rhombus
Für dessen freie Ecken ergibt sich:
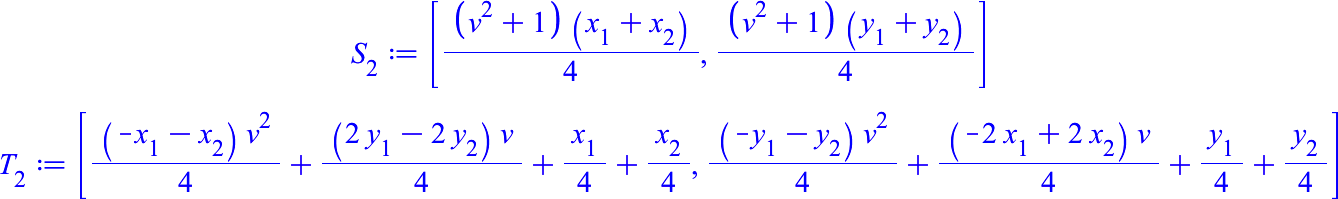
Wir sehen, dass S1 und S2 übereistimmen. Damit ist die Schließungseigenschaft gezeigt.
4 Iteration
Die Abbildung 6 zeigt eine Iteration des Vorgehens.

Abb. 6: Iteration
5 Details
Ohne Beweis einige weitere Eigenschaften.
5.1 Diagonalen
Die beiden Diagonalen (Abb. 7) sind orthogonal. Ihr Längenverhältnis ist v.
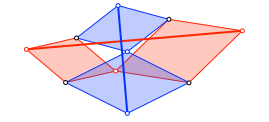
Abb. 7: Diagonalen
Die beiden schwarzen Verbindungen der rot/blau-Gelenkpunkte (Abb. 8) sind gleich lang. Ihr Schnittwinkel ist gleich dem Rhombenwinkel.
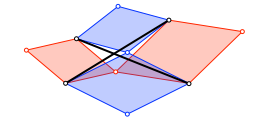
Abb. 8: Verbindungslinien
5.2 Kreise
Drei der vier Ecken eines jeden Rhombus sind gelenkig mit je einem weiteren Rhombus verbunden.
Wir zeichnen den Kreis durch die drei Gelenkpunkte des roten Rhombus links (Abb. 9).
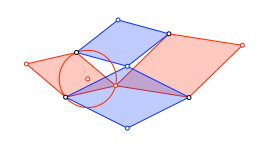
Abb. 9: Kreis durch drei Gelenkpunkte
Entsprechend zeichnen wir die Kreise für die drei anderen Rhomben (Abb. 10). Die vier Kreise verlaufen durch einen gemeinsamen Punkt.
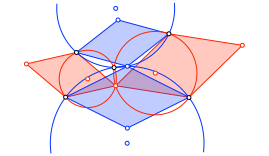
Abb. 10: Vier Kreise durch denselben Punkt
Dieser Punkt ist auch der Schnittpunkt der Verbildungslinien der rot/blauen Gelenkpunkte (Abb. 11).
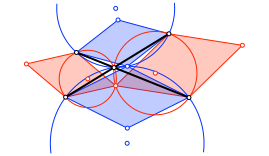
Abb. 11: Schnittpunkt
Die Mittelpunkte der vier Kreise bilden einen Rhombus (Abb. 12). Dieser ist ähnlich zu den vier schon vorhandenen Rhomben.
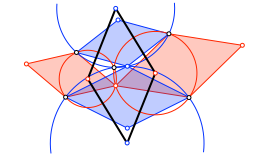
Abb. 12: Weiterer Rhombus
Die Diagonalen dieses Rhombus (Abb. 13) sind parallel zu den Diagonalen der Abbildung 7.
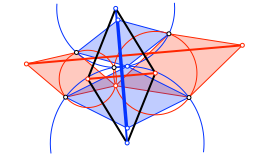
Abb. 13: Parallele Diagonalen
5.3 Mittelpunkte
Die Mittelpunkte der vier Rhomben sind Eckpunkte eines weiteren Rhombus (Abb. 14). Dieser ist ähnlich zu den schon vorhandenen Rhomben.
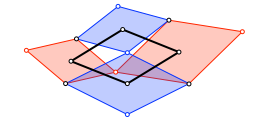
Abb. 14: Noch ein Rhombus
Die Diagonalen dieses weiteren Rhombus (Abb. 15) sind ebenfalls parallel zu den Diagonalen der Abbildung 7.
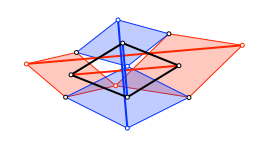
Abb. 15: Parallele Diagonalen
5.4 Eine Gerade
Die Mittelpunkte der beiden neuen Rhomben sowie der rot/rote und der blau/blaue Gelenkpunkt liegen auf einer Geraden (Abb. 16).
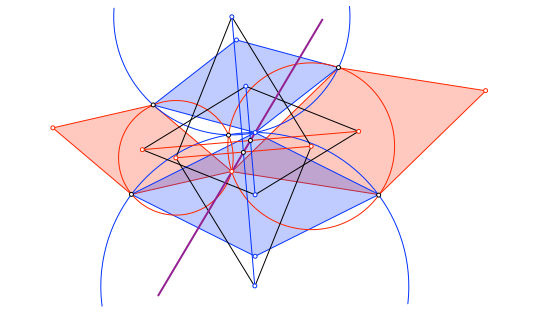
Abb. 16: Vier Punkte auf einer Geraden
5.5 Sonderfall
Im Sonderfall v = 1 erhalten wir Quadrate (Abb. 17). In diesem Sonderfall ist die Flächensumme der roten Quadrate gleich der Flächensumme der blauen Quadrate.

Abb. 17: Quadrate