Hans Walser, [20170723a]
Rhomben im Raster
1 Worum geht es
Wir zeichnen Rhomben im Quadratraster und im Dreiecksraster. Dabei treffen wir auch auf einen grafischen Zugang zu den Formeln der pythagoreischen Dreiecke.
2 Rhombus
Ein Rhombus kann verschieden charakterisiert werden.
In der Regel wird eine der drei folgenden charakterisierenden Eigenschaften als Definition verwendet. Die beiden anderen Eigenschaften mźssen dann als Theorem bewiesen werden.
2.1 Diagonaleneigenschaft
Viereck mit orthogonalen sich halbierenden Diagonalen.
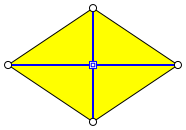
Abb. 1: Diagonalen
Parameter: Die beiden DiagonalenlŠngen
Modell: Heidelberger Kreuz
2.2 Seiteneigenschaft
Viereck mit vier gleich langen Seiten (Abb. 2).
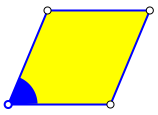
Abb. 2: Seite und Winkel
Parameter: SeitenlŠnge, spitzer Innenwinkel
Gelenkmodell
2.3 Streifen
Durchschnitt zweier gleich breiter Streifen (Abb. 3).
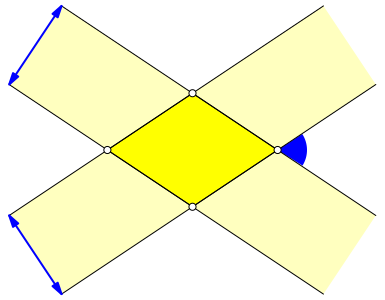
Abb. 3: Zwei Streifen
Parameter: Streifenbreite, spitzer Winkel der Streifen
3 Im Quadratraster
Im Quadratraster (Karoraster) kšnnen Rhomben auf verschiedene Weisen eingezeichnet werden.
Die Abbildung 4 orientiert sich an der Diagonaleneigenschaft. Die Diagonalen sind Rasterlinien.
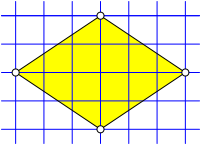
Abb. 4: Diagonaleneigenschaft im Raster
Die Abbildung 5 orientiert sich ebenfalls an der Diagonaleneigenschaft. Die Diagonalen liegen auf schrŠgen Symmetrieachsen des Rasters.
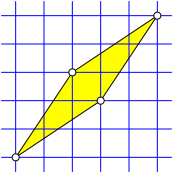
Abb. 5: Diagonalen auf schrŠgen Symmetrieachsen
Die Abbildung 6a operiert ebenfalls mit der Diagonaleneigenschaft.
Wir kšnnen aber auch mit Pythagoras rechnen und die Seiteneigenschaft verwenden (Abb. 6b).
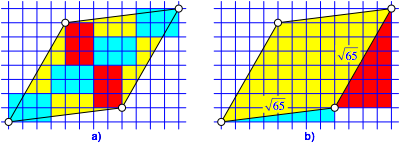
Abb. 6: Diagonaleneigenschaft. Seiteneigenschaft
Die Abbildung 7 zeigt ein zweites Beispiel dieser Art.
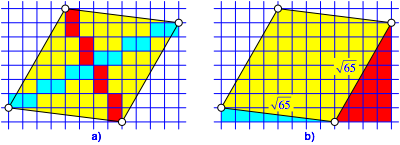
Abb. 7: Weiteres Beispiel
Die Abbildung 8 zeigt noch ein Beispiel.
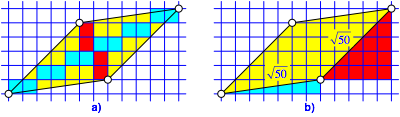
Abb. 8: Noch ein Beispiel
4 Pythagoreische Rhomben
In der Abbildung 9 wind zwei gegenźberliegende Rhombenseiten auf Rasterlinien. Entsprechend verschwindet in der Abbildung 9b das hellblaue rechtwinklige Dreieck. Das rote rechtwinklige Dreieck hat die Katheten 3 und 4 (Lehrerdreieck, pythagoreisches Dreieck).
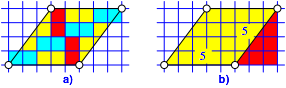
Abb. 9: Pythagoreische Rhombus
Rhomben dieser Art nennen wir pythagoreische Rhomben.
Die Abbildung 10 zeigt das nŠchste Beispiel. Das pythagoreische Dreieck hat die Katheten 5 und 12.
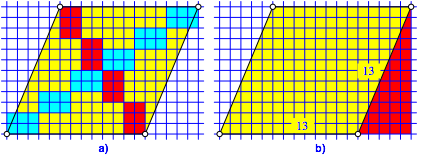
Abb. 10: NŠchstes Beispiel
Wir sehen, wie der Hase lŠuft.
Wir wŠhlen zwei natźrliche Zahlen 0 < v < u und bilden damit einerseits Rechtecke im Querformat (hellblau) und im Hochformat (rot).
Von einem Rasterpunkt aus bilden wir mit je u hellblauen Rechtecken eine gemŠchliche Treppe nach rechts oben beziehungsweise nach links unten. Weiter bilden wir mit je v roten Rechtecken eine steile Treppe nach links oben beziehungsweis nach rechts unten.
Wegen uv = vu źberwinden die blaue und die rote Treppe dieselbe Hšhendifferenz 2uv. Wir erhalten also einen Rhombus mit zwei Rasterlinien als Seiten. Die schrŠgen Rhombenseiten haben ein pythagoreisches Dreieck als Stźtzdreieck.
Die
horizontale Rhombenseite ist 
. Das ist dann auch die HypotenusenlŠnge des
pythagoreischen Dreieckes. Die gesamte Treppenhšhe ist 2uv. Dies ist die Hšhe des Rhombus und damit auch die senkrechte
Kathete des pythagoreischen Dreieckes. Der ă†berhangŇ des Rhombus ist 
. Dies ist die kurze Kathete des pythagoreischen
Dreieckes.
Wir haben also die bekannten Formeln (in Standardschreibweise) neu gefunden:
(1)
5 Im Dreiecksraster
Die Diagonaleneigenschaft des Rhombus lŠsst sich im Dreiecksraster weniger gut einsetzen. Gleichwohl gibt es triviale Lšsungen (Abb. 11).
Abb. 11: Triviale Lšsungen
Fźr den Sonderfall eines spitzen Winkels von 60ˇ gibt es ebenfalls viele Lšsungen (Abb. 12).
Ab. 12: Spitzer Winkel 60ˇ
Die Abbildung 13 zeigt ein ăpythagoreischesŇ Bespiel.
Abb. 13: ăPythagoreischesŇ Beispiel
Das rote Dreieck hat die kurzen Seiten 3 und 5 und den stumpfen Winkel 120ˇ. Fźr die lŠngste Seite liefert der Kosinussatz die LŠnge 7.
Es ist also ein ăpythagoreischesŇ 120ˇ-Dreieck.
Die Abbildung 14 zeigt ein zweites Beispiel dieser Art. Die Seiteneigenschaft kann wiederum mit dem Kosinussatz nachgewiesen werden.
Abb. 14: Pythagoreischer Rhombus
Es ist mir nicht gelungen, die zu (1) analogen Formeln visuell zu zeigen.
Die zu (1) analogen Formeln lauten:
(2)
Der Nachweis von (2) geschieht mit dem Kosinussatz.
Im Beispiel der Abbildung 13 ist u = 2 und v = 1.
Im Beispiel der Abbildung 14 ist u = 3 und v = 1.