Hans Walser, [20180414]

Rhombendodekaeder

1     Worum geht es?

Konstruktion einer einparametrigen Schar von Rhombendodekaedern. Sie enthŠlt das Rhombendodekaeder zweiter Art, aber nicht das Rhombendodekaeder erster Art.

2     Eckpunktkoordinaten

Die Abbildung 1 zeigt die Situation fŸr den Parameterwert p = 2.

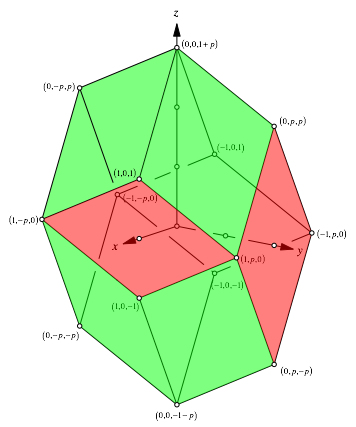
Abb. 1: Koordinaten der Eckpunkte

3     Beschreibung

Das Rhombendodekaeder enthŠlt vier untereinander kongruente Rhomben (rot in Abb. 1 und 2a) mit dem DiagonalenverhŠltnis

 

                                                                   *                                                              (1)

 

 

und dem (in der Abbildung 1 spitzen) Winkel

 

                                                                                                             (2)

 

 

Ferner enthŠlt es acht weitere untereinander kongruente Rhomben (grŸn in Abb. 1 und 2a) mit dem DiagonalenverhŠltnis

 

                                                                                                (3)

 

 

und dem spitzen Winkel:

 

                                                                                                         (4)

 

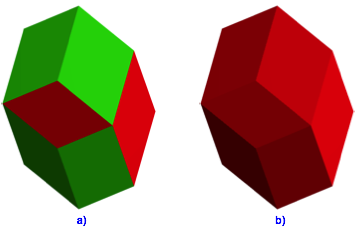
Abb. 2: Rhombendodekaeder, p = 2. Zweifarbig und monochrom

Die Abbildung 2b zeigt dieselbe Figur monochrom.

 

4     RaumfŸller

Das Rhombendodekaeder ist fŸr jedes p ein RaumfŸller. Die Abbildung 3 zeigt die Situation fŸr p = 2.

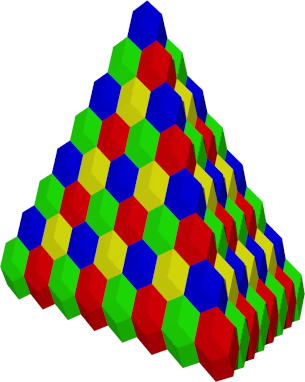
Abb. 30: RaumfŸller

5     SonderfŠlle

5.1    p = 1

FŸr p = 1 erhalten wir vier Quadrate und acht Rhomben mit einem spitzen Winkel von 60¡ (Abb. 4).

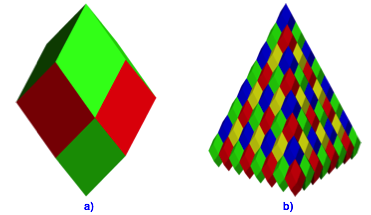
Abb. 4: p = 1

5.2    Goldener Schnitt

Wenn wir zwšlf kongruente Rhomben haben wollen, mŸssen die VerhŠltnisse (1) und (3) Ÿbereinstimmen:

 

                                                                                                                   (5)

 

 

 

Aus (5) erhalten wir:

 

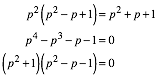                                                                                     (6)

 

 

 

 

Die Gleichung (6) hat die Lšsungsmenge:

 

                                                                         (7)

 

 

Die positive reelle Lšsung ist der Goldene Schnitt (Walser 2013):

 

                                                                                                   (8)

 

 

Das resultierende Rhombendodekaeder wird als Rhombendodekaeder zweiter Art bezeichnet. Es wurde von Bilinski (1960) beschrieben (Abb. 5).

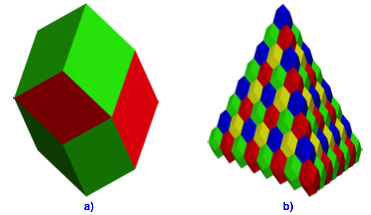
Abb. 5: Rhombendodekaeder zweiter Art

5.3    Quadratwurzel aus 2

Im Rhombendodekaeder erster Art haben wir ein DiagonalenverhŠltnis  (Abb. 6).

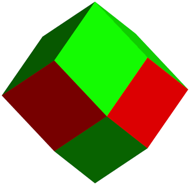
Abb. 6: Rhombendodekaeder erster Art

Beim Rhombendodekaeder erster Art sind sŠmtliche Rhomben kongruent. Die roten €quatorrhomben sind alle ãliegendÒ.

Wir setzen nun bei unserem Rhombendodekaeder  (Abb. 7). Jeder zweite €quatorrhombus ist ãstehendÒ. Die grŸnen Rhomben sind nicht kongruent zu den roten.

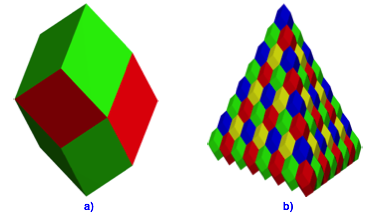
Abb. 7: Quadratwurzel aus 2

Die Rhombendodekaeder der Abbildungen 6 und 7a kšnnen nicht mit einer affinen Abbildung ineinander ŸbergefŸhrt werden.

 

Literatur

Bilinski, Stanko (1960): †ber Rhombenisoeder. Glasnik mat.-fiz. i astr. 15, 1960, No. 4, S. 251-262.

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.