Hans Walser, [20220720]

Rhombenhexaeder

1 Problemstellung

Die Abbildung 1 zeigt zwei Figuren, die aus je sechs kongruenten Rhomben zusammengesetzt sind.

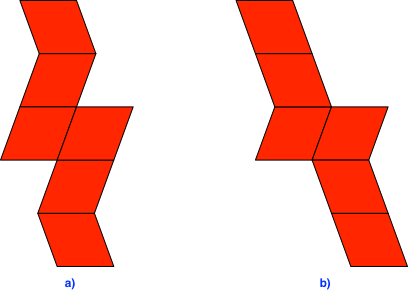
Abb. 1: Rhombenfiguren

Wir können jede dieser Figuren als Abwicklung eines von sechs kongruenten Rhomben begrenzten Körpers (eines Rhombenhexaeders) interpretieren.

Frage: Sind die beiden Rhombenhexaeder kongruent?

2 Bearbeitung

Die beiden Rhombenhexaeder sind nicht kongruent.

Eine ausführliche Studie über Rhombenhexaeder findet sich hier.

2.1 Unterschiedliche Winkelstruktur an den Ecken

In den Abwicklungen (Abb. 3) sind die Ecken in der bei Hexaedern, insbesondere bei Würfeln (Abb. 2), üblichen Reihenfolge beschriftet.

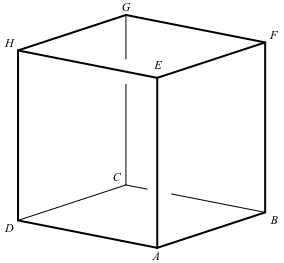
Abb. 2: Eckenbeschriftung beim Würfel

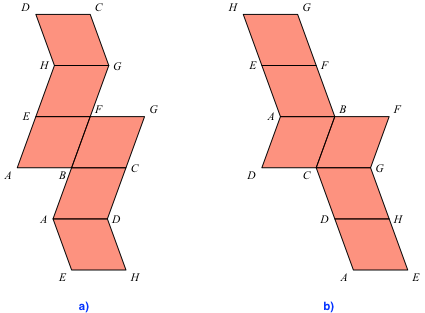
Abb. 3: Entsprechende Beschriftung der Ecken der Rhombenhexaeder

Wir sehen nun folgendes:

a) Im Beispiel a) haben wir zwei diametrale Ecken, nämlich A und G, bei denen ausschließlich spitze Rhombenwinkel liegen. Bei den sechs übrigen Ecken kommen je ein spitzer und zwei stumpfe Rhombenwinkel vor. Wir bezeichnen dieses Rhombenhexaeder als spitzes Rhombenhexaeder.

b) Im Beispiel b) ist es genau umgekehrt. Wir haben zwei diametrale Ecken, nämlich A und G, bei denen ausschließlich stumpfe Rhombenwinkel liegen. Bei den sechs übrigen Ecken kommen je ein stumpfer und zwei spitze Rhombenwinkel vor. Wir bezeichnen dieses Rhombenhexaeder entsprechend als stumpfes Rhombenhexaeder.

Wegen der unterschiedlichen Winkelstruktur an den Ecken sind die beiden Rhombenhexaeder nicht kongruent.

2.2 Unterschiedliches Volumen

Für das Volumen eines Rhombenhexaeders der Kantenlänge 1 und mit drei gleichen Rhombenwinkeln w an zwei diametralen Ecken erhält man nach einiger Rechnung die Formel:

In unserem Beispiel a) des spitzen Rhombenhexaeders ist der spitze Winkel w = 70° und entsprechend im Beispiel b) des stumpfen Rhombenhexaeders der stumpfe Winkel w = 110°.

Die Tabelle 1 zeigt, dass das spitze Rhombenhexaeder das größere Volumen hat.

w	Volumen	Bemerkungen
0°	0	Strecke
10°	0.0261801496
20°	0.1023340925
30°	0.2214454910
40°	0.3722826858
50°	0.5400379424
60°	0.7071067810	Oktaeder mit zwei diametral angesetzten Tetreaedern. √(½)
70°	0.8538642625	Spitzes Rhombenhexaeder der Abb. 1a
80°	0.9591721420
90°	1	Würfel
100°	0.9481912596
110°	0.7543534670	Stumpfes Rhombenhexaeder der Abb. 1b
120°	0	Plattes regelmäßiges Sechseck

Tab. 1: Volumina

2.3 Modelle

Die Abbildung 4 zeigt je ein Papiermodell des spitzen (links) und des stumpfen (rechts) Rhombenhexaeders mit kongruenten Seitenrhomben. Wir sehen deutlich, dass das spitze Rhombenhexaeder höher ist. Bei kongruenten Grundflächen bedeutet dies ein größeres Volumen.

Abb. 4: Papiermodelle

Die Papiermodelle der Abbildung 4 sind mit den Schnittmustern der Abbildungen 5a und 5b gebaut worden.

2.4 Schnittmuster

Abb. 5a: Schnittmuster spitzes Rhombenhexaeder

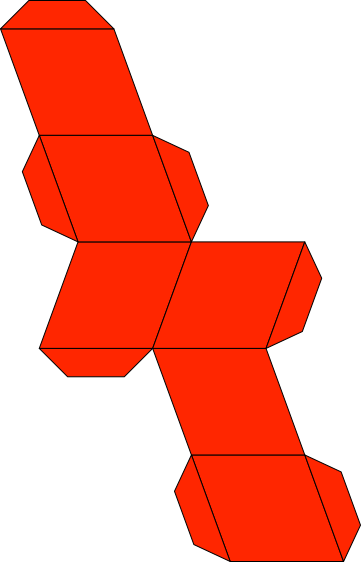
Abb. 5b: Schnittmuster stumpfes Rhombenhexaeder

Weblink

Hans Walser: Rhombenhexaeder

http://www.walser-h-m.ch/hans/Miniaturen/R/Rhombenhexaeder2/Rhombenhexaeder2.html