1 What about?

Construction of the rhombic dodecahedron in the cube using diagonals.

2 Procedure

We draw the diagonals of the faces of a cube and intersect them (Fig. 1). Of course, the resulting six points are also the centers of the faces of the cube.

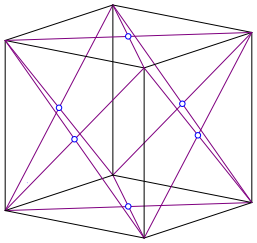
Fig. 1: Centers of the faces

The six points are the vertices of an octahedron (Fig. 2). The octahedron is the dual to the cube.

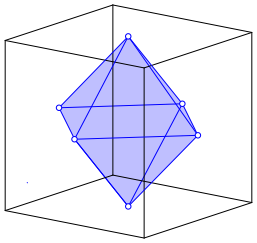
Fig. 2: Octahedron dual to the cube

Together with the diagonals of figure 1 we get the Kepler star (stella octangula, fig. 3 and 4).

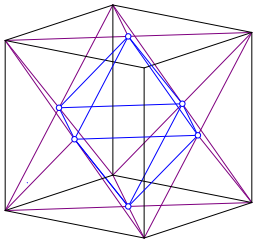
Fig. 3: Kepler star

Fig. 4: Kepler star

We get the Kepler star also by placing a tetrahedron on each side of the octahedron.

Back to the cube: we draw the room diagonals and divide them into four parts (Fig. 5).

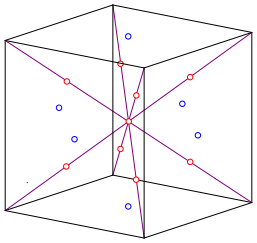
Fig. 5: Room diagonals

The outer dividing points are the vertices of a cube of half the length of the initial cube (Fig. 6).

These points are also the centers of the attached tetrahedra of the Kepler star.

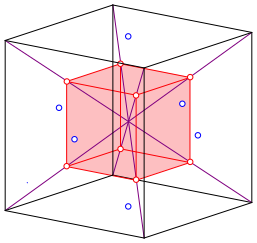
Fig. 6: Cube in the cube

The eight red vertices of the cube and the six blue vertices of the octahedron are the vertices of a rhombic dodecahedron (Fig. 7). The proof is left to the reader.

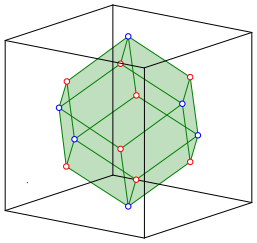
Fig. 7: Rhombic dodecahedron

The volume of the rhombic dodecahedron is one quarter of the cube volume.

Reference

Knoll, Eva and Morgan, Simon (2003): Finding the Dual of the Tetrahedral-Octahedral Space Filler. Meeting Alhambra, ISAMA-BRIDGES Conference Proceedings (2003). Pages 205–212.