Hans Walser, [20210603]
Rohrpost
1 Worum geht es?
Spielerei mit Rohrprofilen.
2 Rohrsysteme
Die Rohre der Abbildungen 1, 2 und 3 haben einen runden, einen quadratischen und einen auf der Kante stehenden quadratischen Querschnitt.
Das erste Rohrstck liegt auf einer horizontalen Ebene, das zweite ebenfalls, aber im rechten Winkel zum ersten, und das dritte steht senkrecht.
Dir Rohrwinkel sind alle auf Gehrung gearbeitet.

Abb. 1: Runder Querschnitt

Abb. 2: Quadratischer Querschnitt

Abb. 3: Die ersten beiden Rohre liegen auf einer Kante
3 Problemstellung
Wir fragen bei jedem Rohrquerschnitt nach dem volumenm§ig gr§ten Krper, der durch das Rohr geschoben werden kann.
4 Quadratischer Querschnitt
Beim quadratischen Querschnitt (Abb. 2) ist die Lsung offensichtlich ein Wrfel mit gleicher Kantenlnge wie der Querschnitt (Abb. 4).

Abb. 4: Wrfel
Die Kugel, welche in der Abbildung 2 durchgeht, ist die Inkugel des Wrfels der Abbildung 4.
5 Rohre auf Kante
5.1 Versuch mit einem Wrfel
Wenn die ersten beiden Rohre auf einer Kante liegen (Abb. 3) wird man ja wohl auch den Wrfel auf eine Kante stellen mssen (Abb. 5).
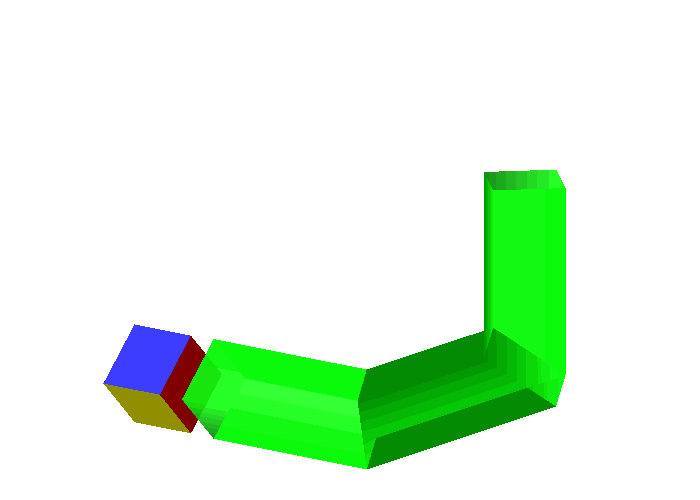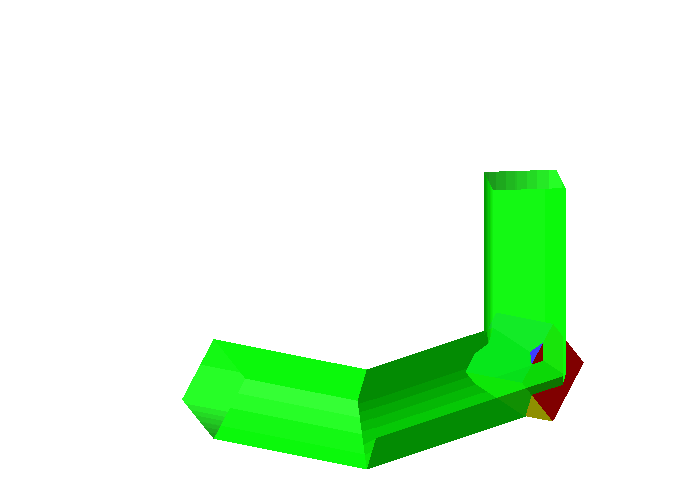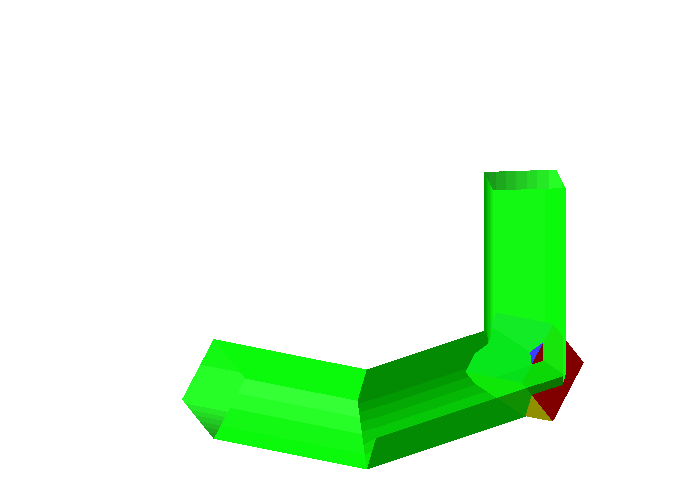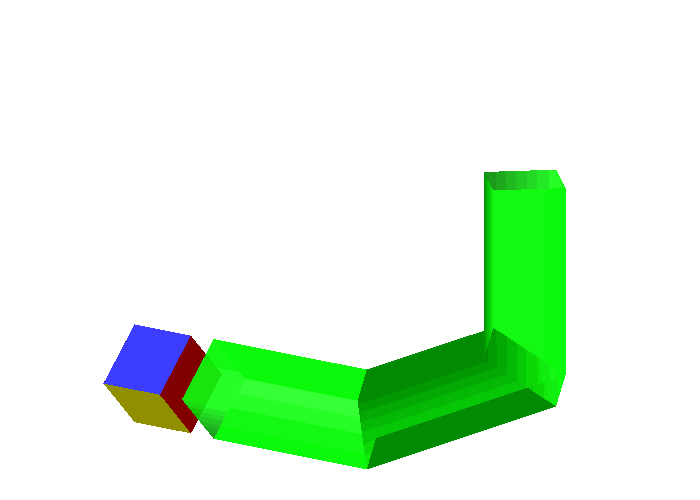
Abb. 5: Versuch mit Wrfel
So geht es nicht. Der Wrfel ist zu gro§. Wir mssten ihn in den Ecken drehen knnen. Da er aber dort verkantet, ist dies nicht mglich.
5.2 Oktaeder
Erinnern wir uns an das Oktaeder (Abb. 6).
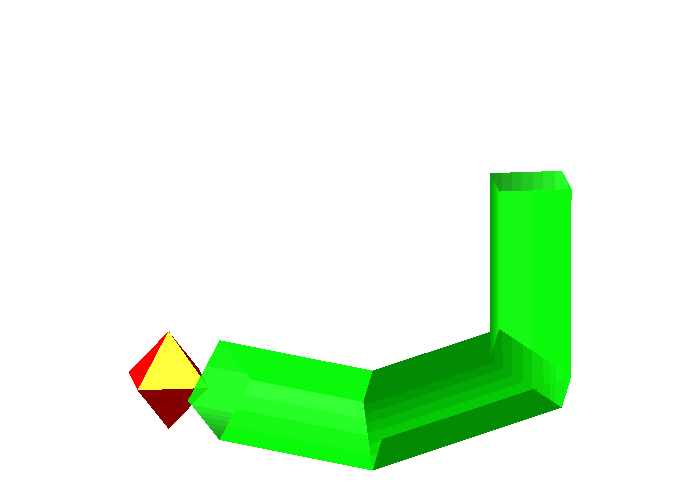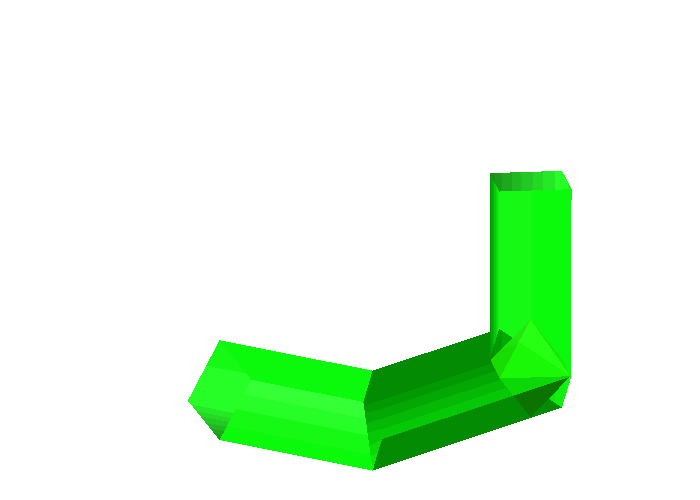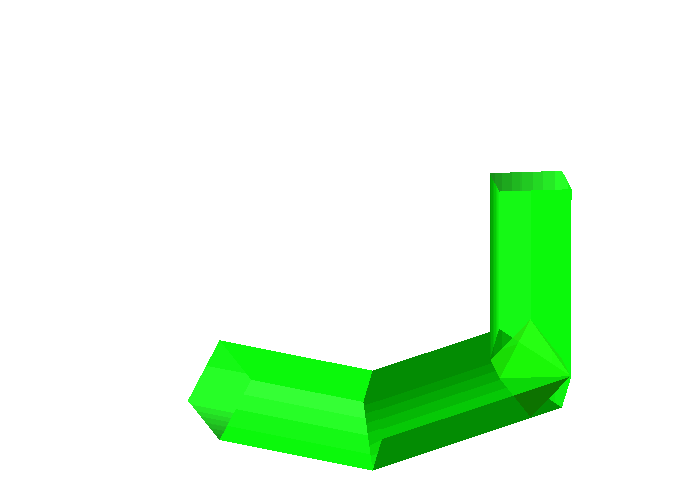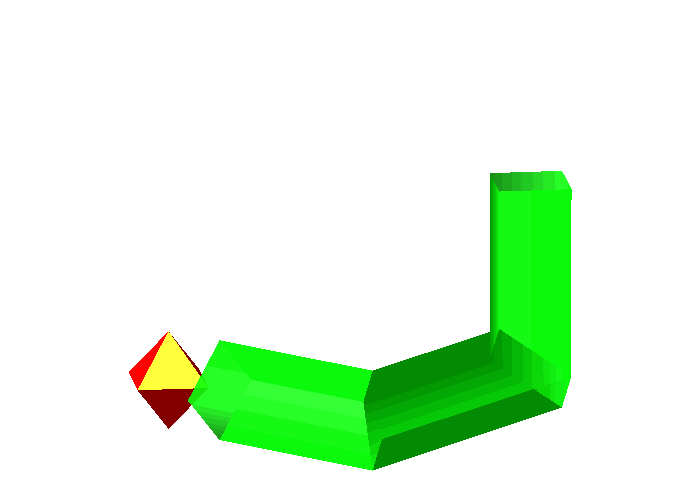
Abb. 6: Oktaeder
Es funktioniert. Das Oktaeder fllt jeweils den ganzen Querschnitt eines jeden Rohrteils. Allerdings sind es nur die Kanten, welche die Rohrwnde von innen berhren.
5.3 Rhombendodekaeder
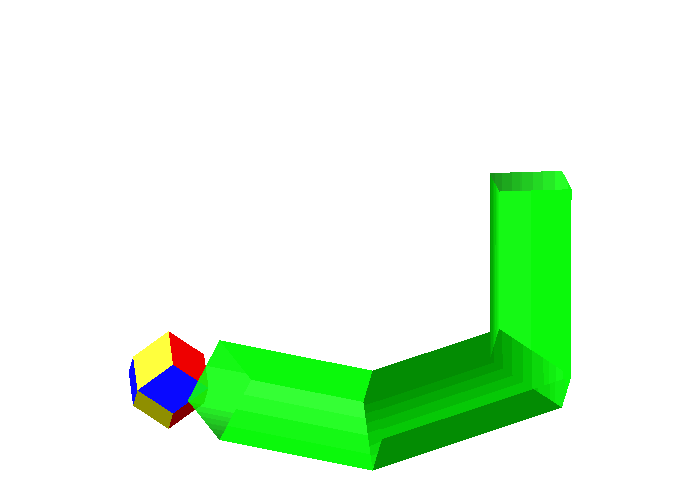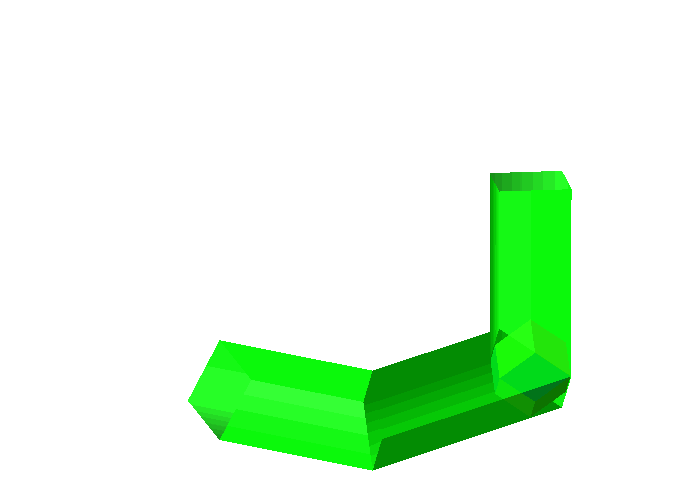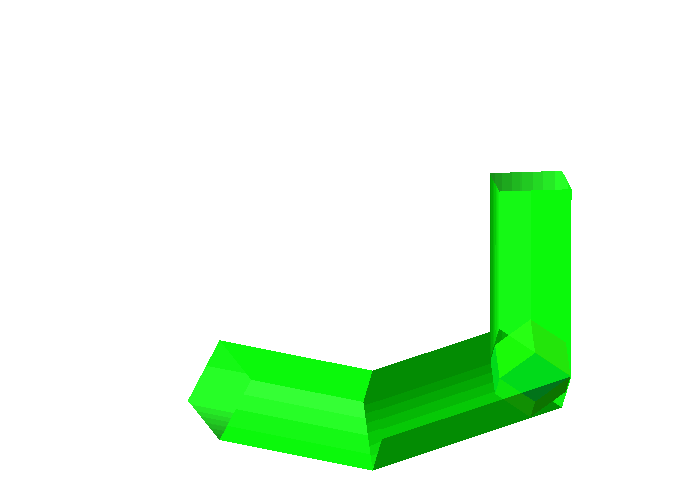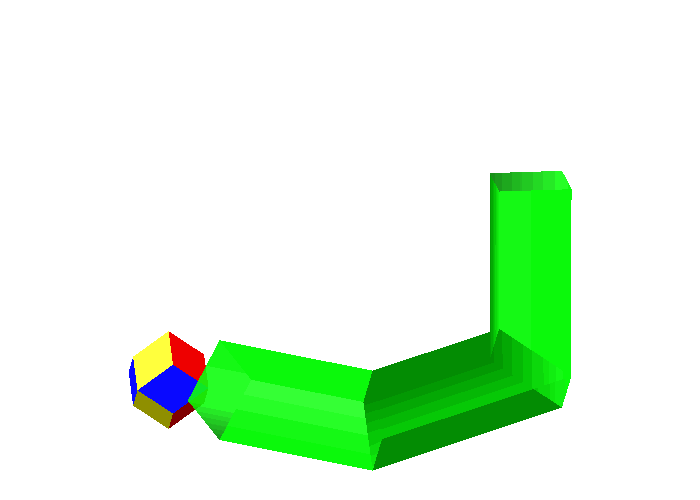
Abb. 7: Rhombendodekaeder
Die Abbildung 8 zeigt das Rhombendodekaeder vergr§ert.
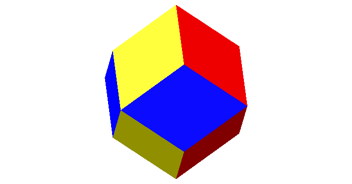
Abb. 8: Rhombendodekaeder
Das Rhombendoekaeder berhrt die Rohrwnde jeweils auf Rhombenflchen. Im ersten Rohrteil sind es die gelben Rhomben, im mittleren Rohrteil die roten Rhomben und im senkrechten Rohrteil die blauen.
Die langen Diagonalen der Rhomben bilden ein Oktaeder, welches im Rhombendodekaeder sitzt. Es ist das Oktaeder der Abbildung 6.
Die Kugel, welche in der Abbildung 3 durchgeht, ist die Inkugel des Rhombendodekaeders.
5.4 Kleiner Wrfel, aber vermutlich der gr§tmgliche
Die kurzen Diagonalen der Rhomben bilden einen Wrfel, welcher ebenfalls im Rhombendodekaeder sitzt. Mit diesem Wrfel kommen wir durch (Abb. 9). Ich vermute, dass dies der gr§te Wrfel ist, mit dem wir ohne Anecken durchkommen.
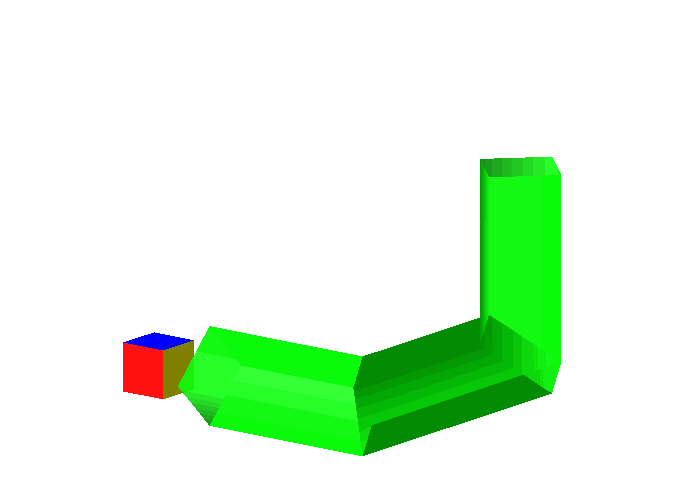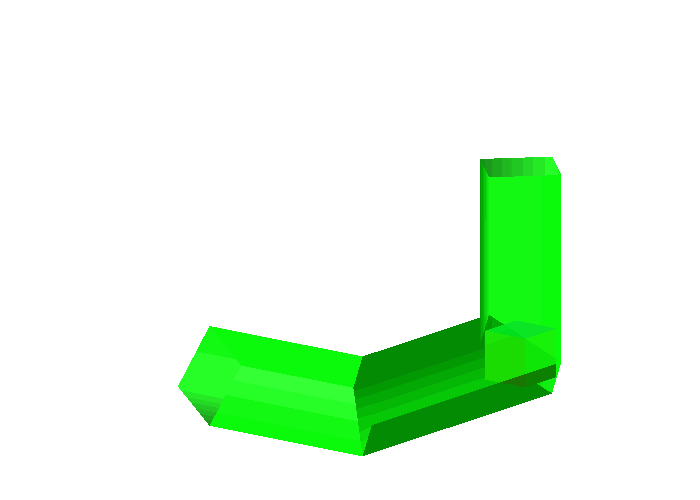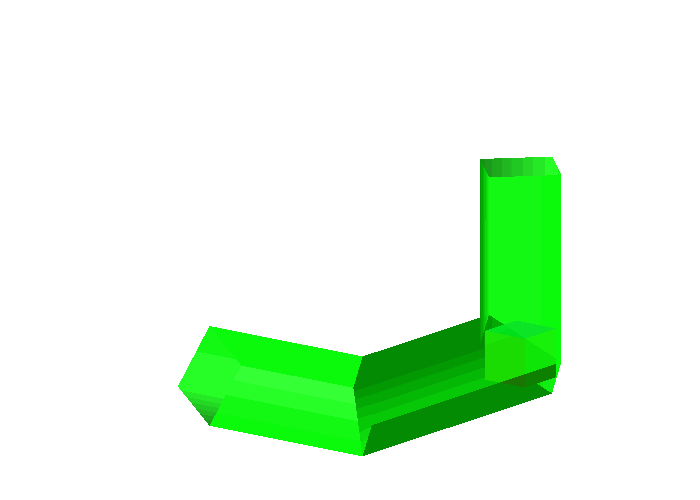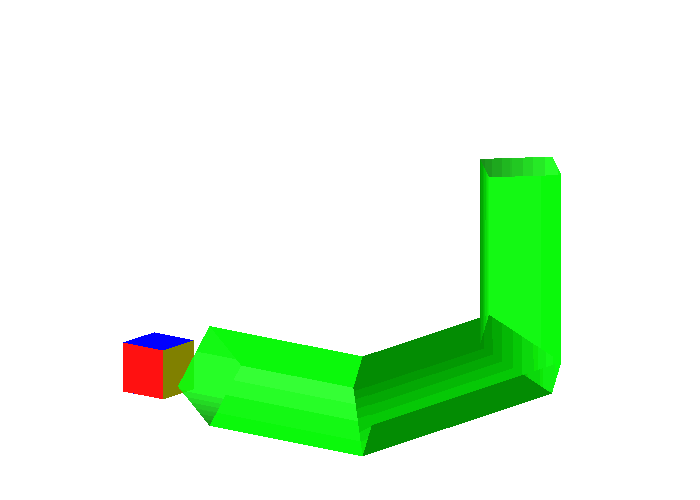
Abb. 9: Kleiner Wrfel
6 Runder Querschnitt
6.1 Kugel
Natrlich geht es mit der Kugel (Abb. 1 und 10). Allerdings berhrt die Kugel die Innenseite der Rohre immer nur lngs eines Gro§kreises. In den Ecken ist noch Luft drin.
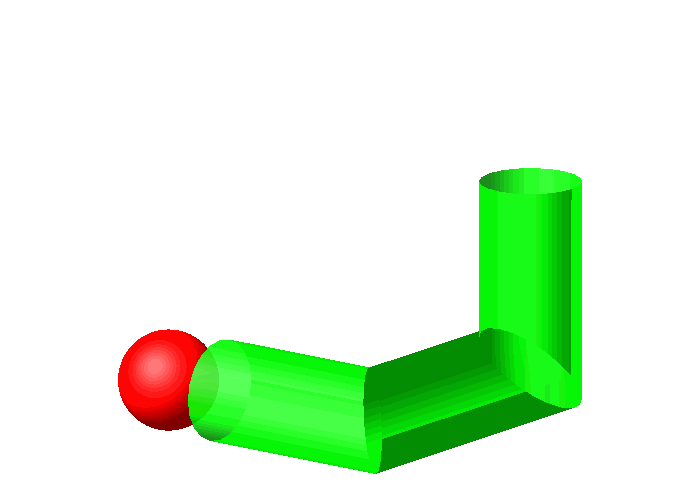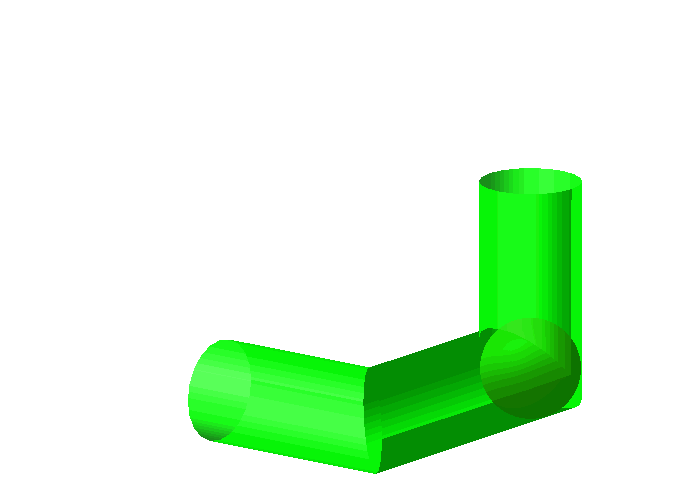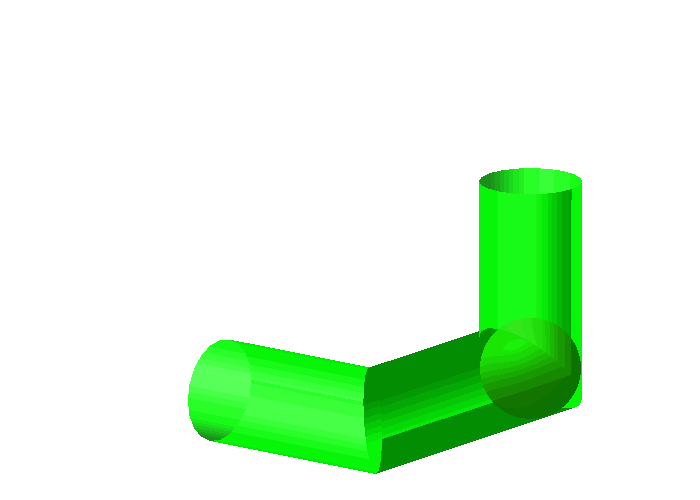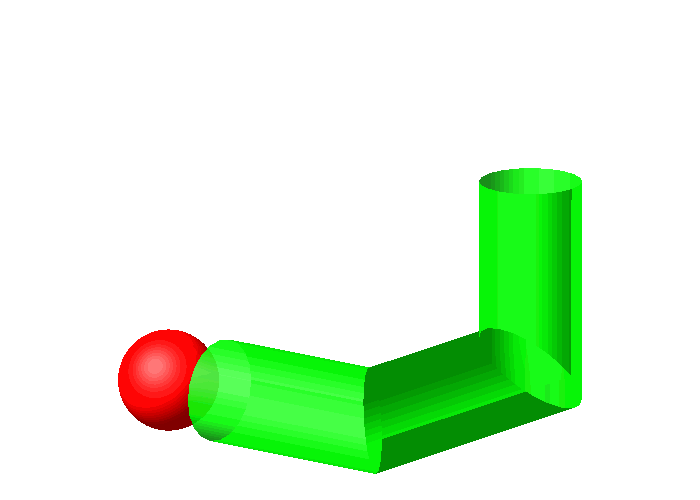
Abb. 10: Kugel im Rohr
6.2 Sphroid
Besser geht es mit dem Sphroid.
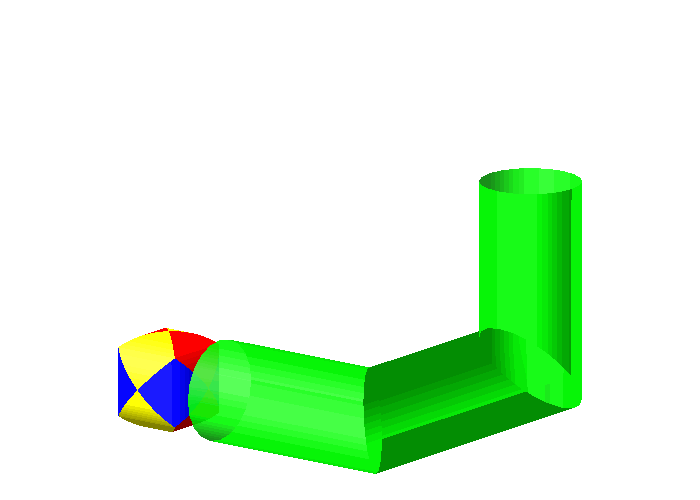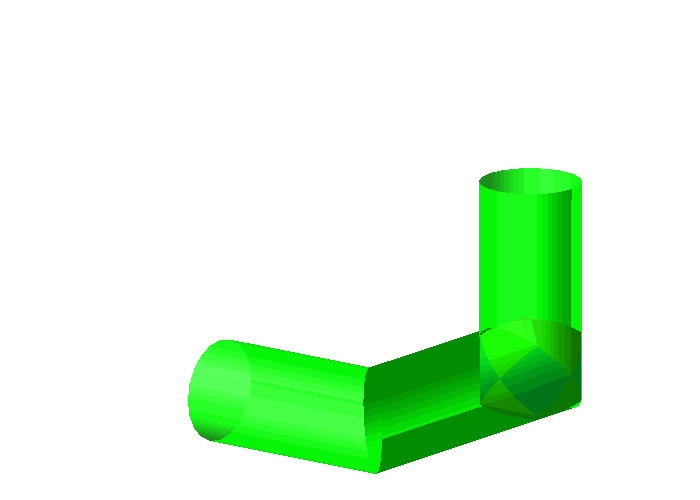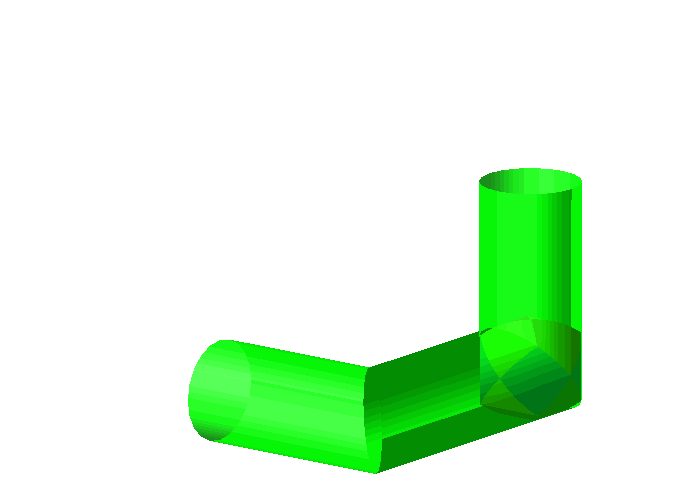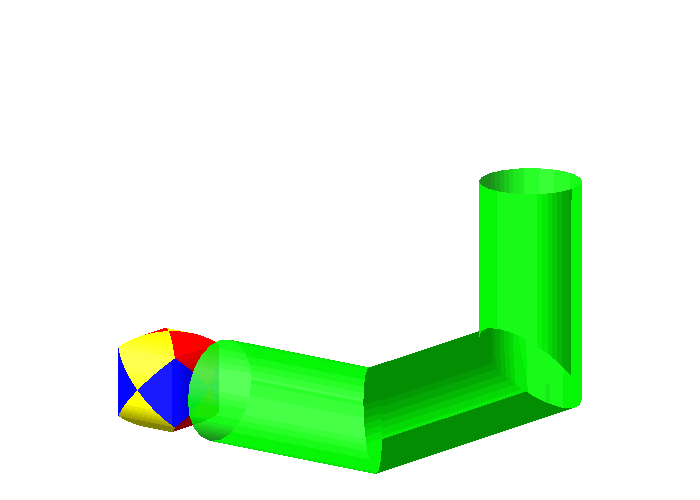
Abb. 11: Sphroid
Die Abbildung 12 zeigt das Sphroid vergr§ert. Die Verwandtschaft mit dem Rhombendodekaeder ist offensichtlich.
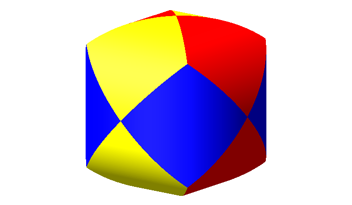
Abb. 12: Sphroid
Das Sphroid ist der volumenm§ig gr§te Krper, der noch durchs Rohrsystem geht.
Websites
Hans-Jrgen Elschenbroich: Konoid
https://www.geogebra.org/m/y57fhddh
Hans-Jrgen Elschenbroich: Konoid 2
https://www.geogebra.org/m/gqfnnhfe
Hans-Jrgen Elschenbroich: Konoidmantel
https://www.geogebra.org/m/y57fhddh
Hans Walser: Dreitafelprojektion
http://www.walser-h-m.ch/hans/Miniaturen/D/Dreitafelprojektion/Dreitafelprojektion.htm
Hans Walser: Hyperboloid-Stern
http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperboloid-Stern/Hyperboloid-Stern.htm
Hans Walser: Pyramidoid
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyramidoid/Pyramidoid.htm
Hans Walser: Paraboloid-Stern
http://www.walser-h-m.ch/hans/Miniaturen/P/Paraboloid-Stern/Paraboloid-Stern.htm
Hans Walser: Rund ohne ¹
http://www.walser-h-m.ch/hans/Miniaturen/R/Rund_ohne_Pi/Rund_ohne_Pi.htm
Hans Walser: Sphroid
http://www.walser-h-m.ch/hans/Miniaturen/S/Sphaeroid/Sphaeroid.htm