Hans Walser, [20210921]
Rosetten
Anregung: Klaus-Anton
0 Worum geht es?
Spiel mit Rosetten und regelmäßigen Vielecken
Mathematischer Hintergrund: n + (n + 1) = 2n + 1
1 Beispiele
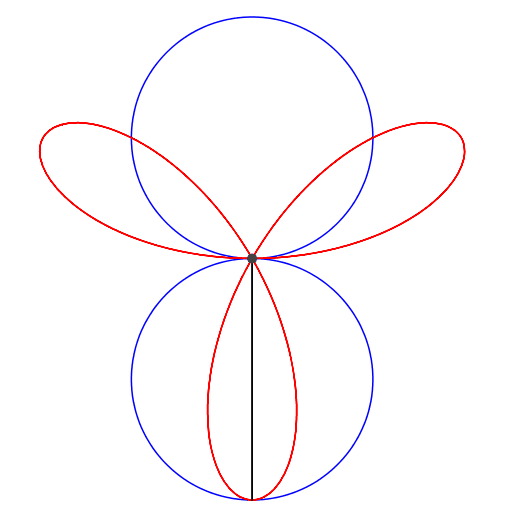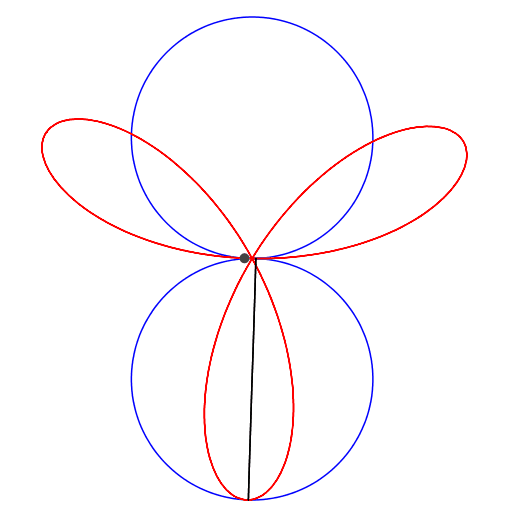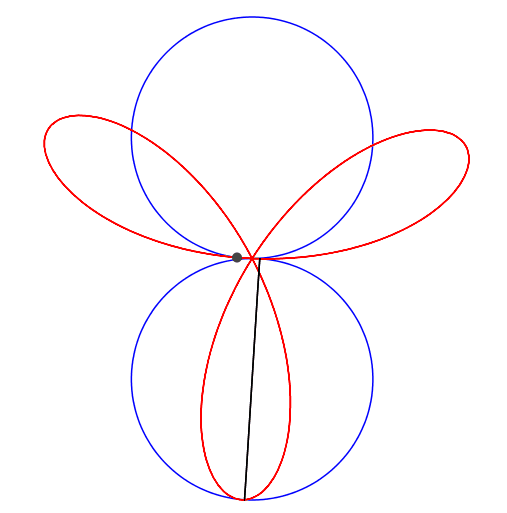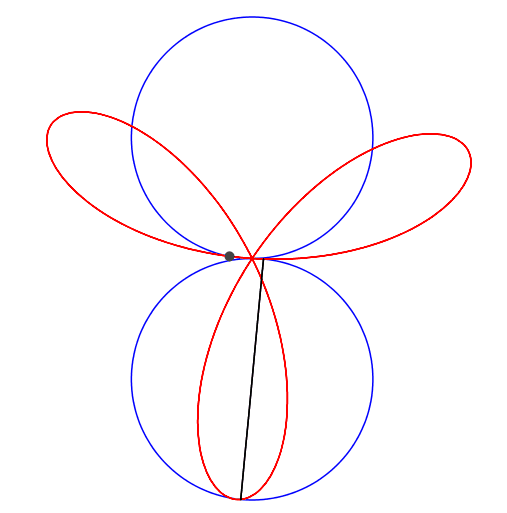
Abb. 1: 1 + 2 = 3
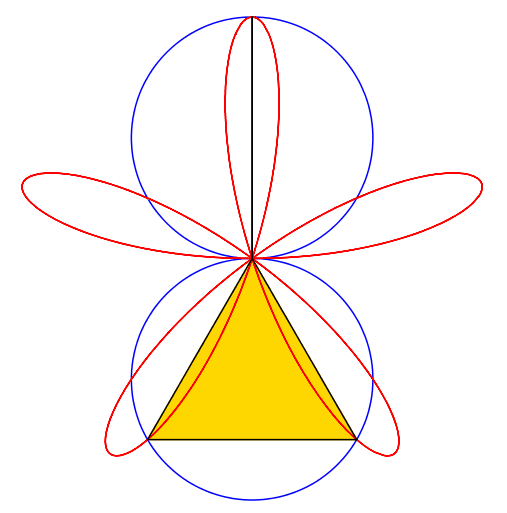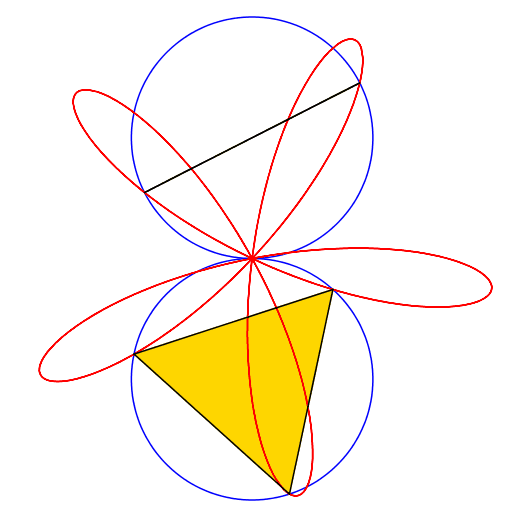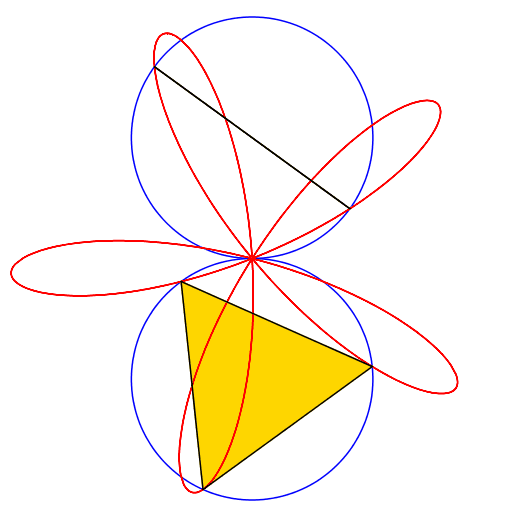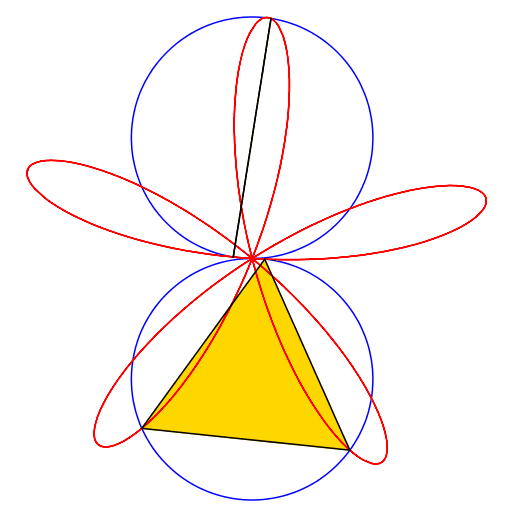
Abb. 2: 2 + 3 = 5
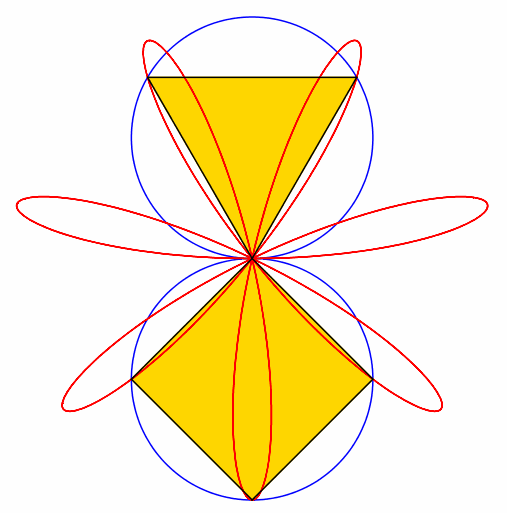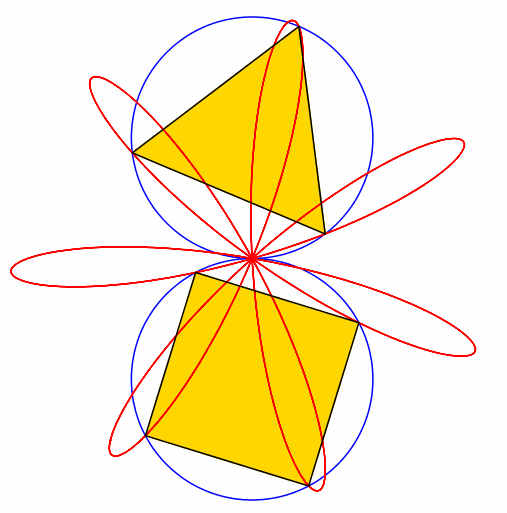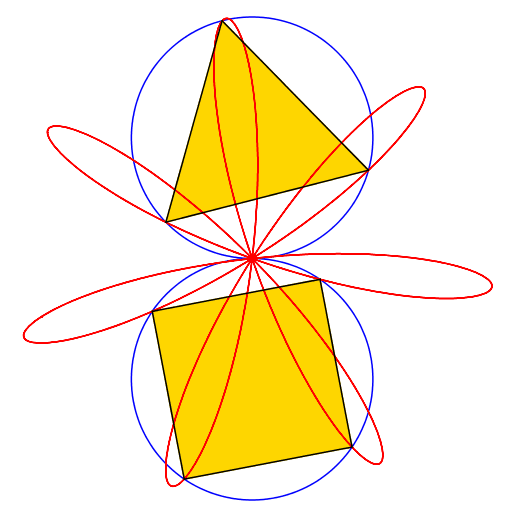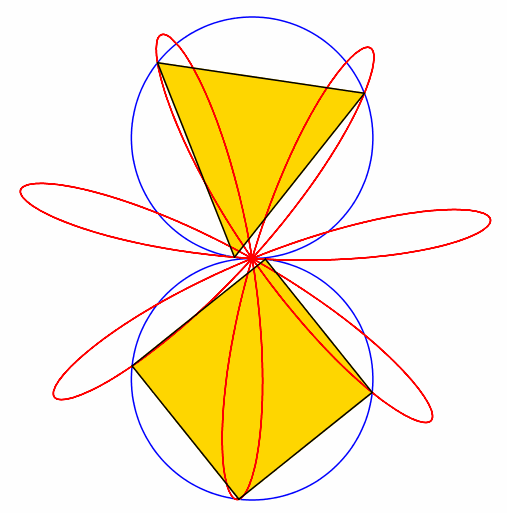
Abb. 3: 3 + 4 = 7
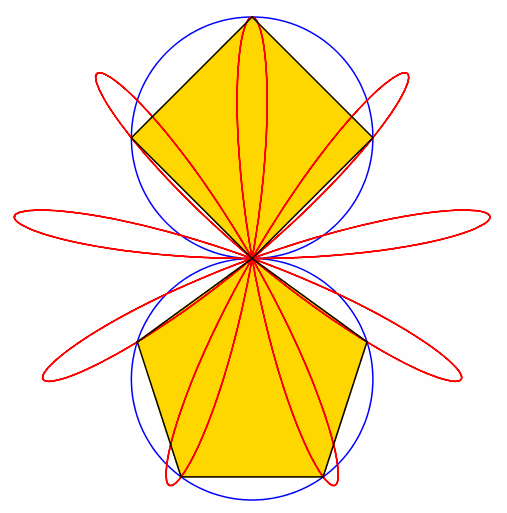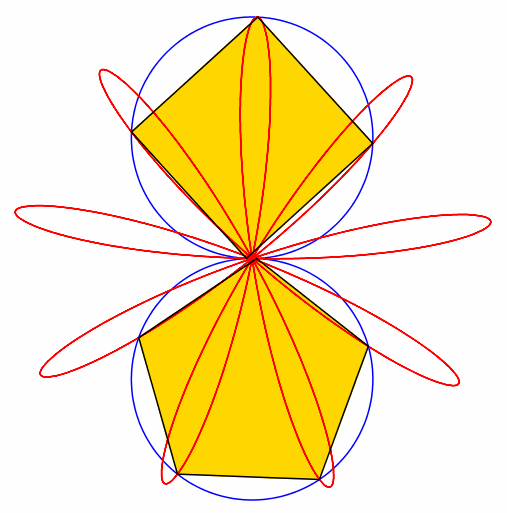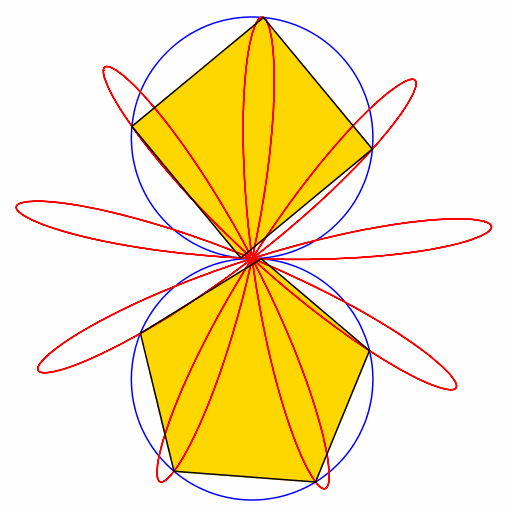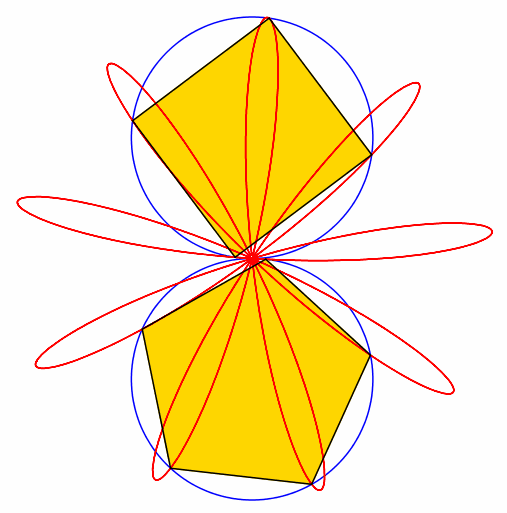
Abb. 4: 4 + 5 = 9
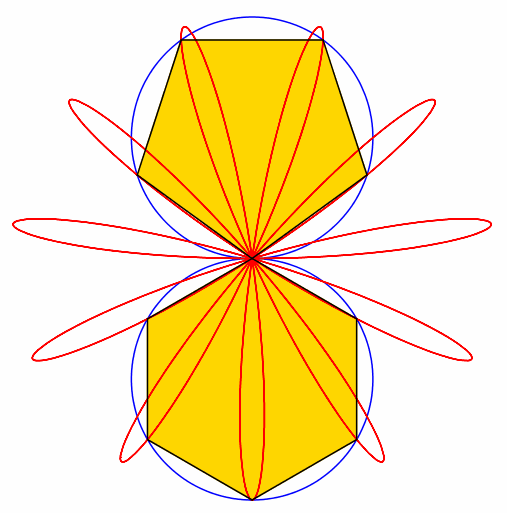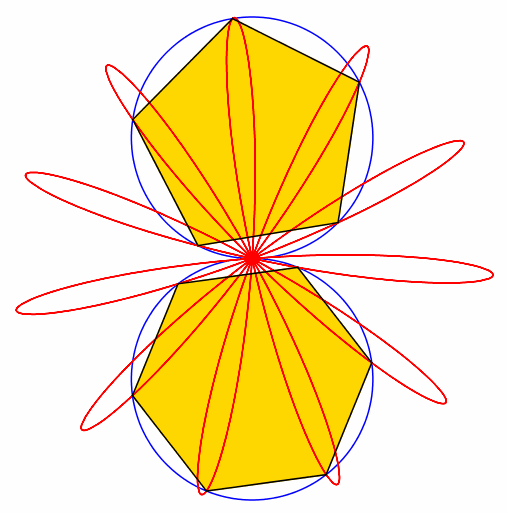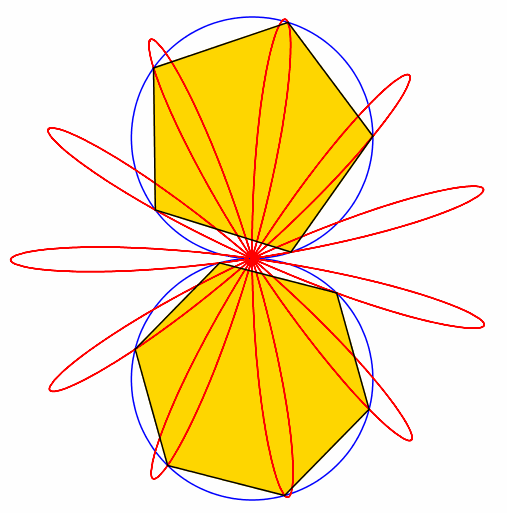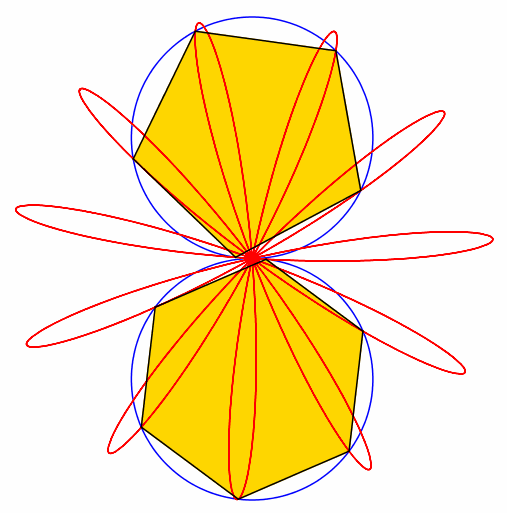
Abb. 5: 5 + 6 = 11
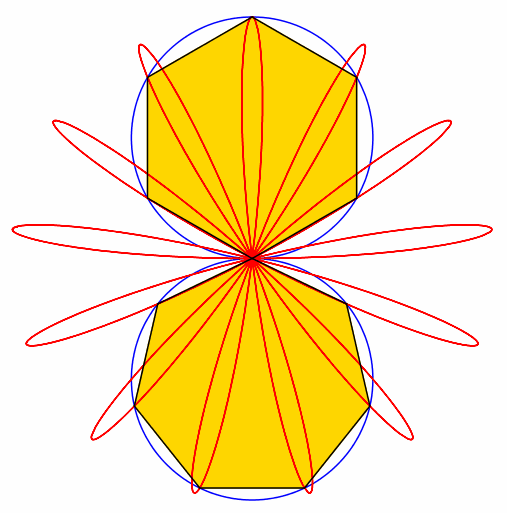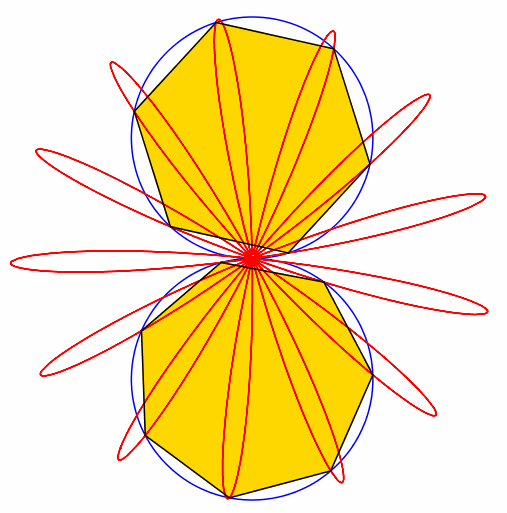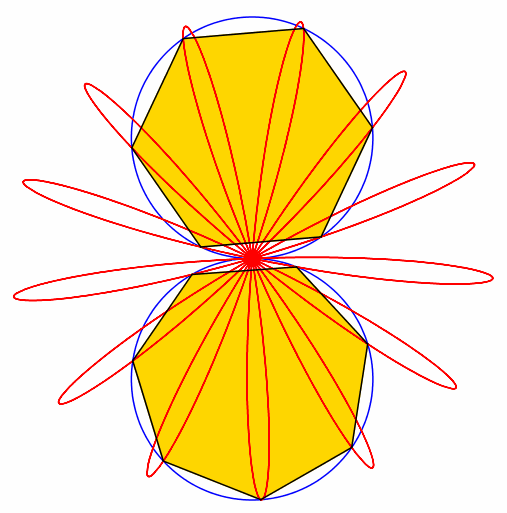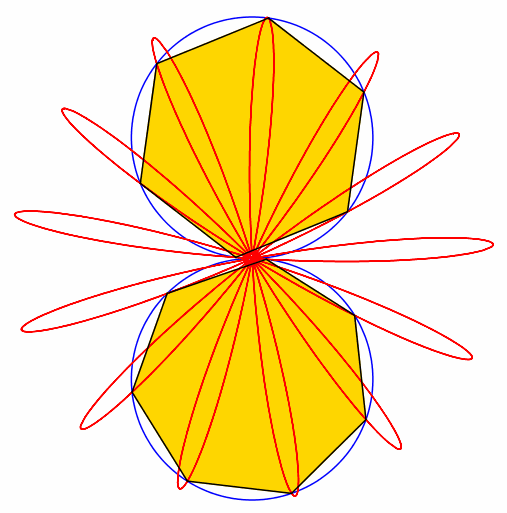
Abb. 6: 6 + 7 = 13
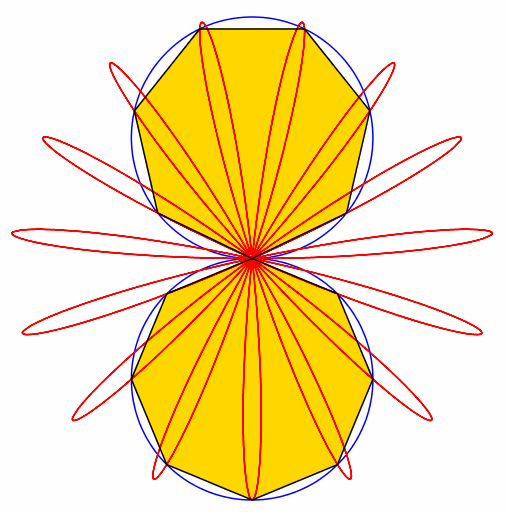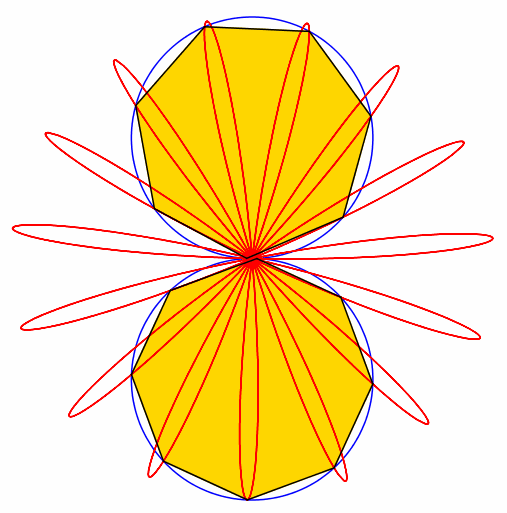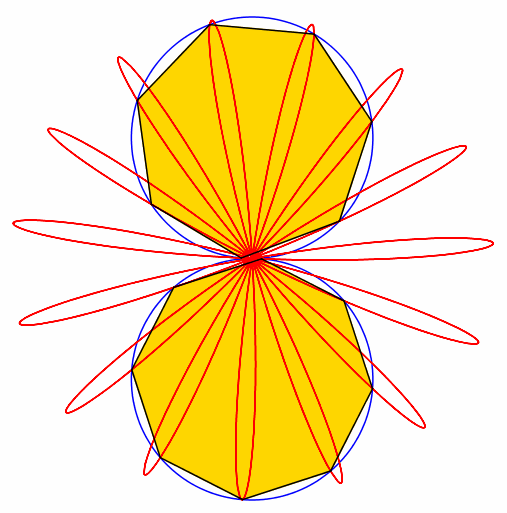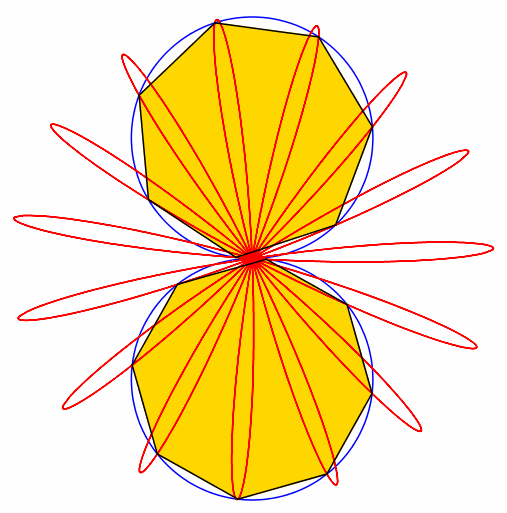
Abb. 7: 7 + 8 = 15
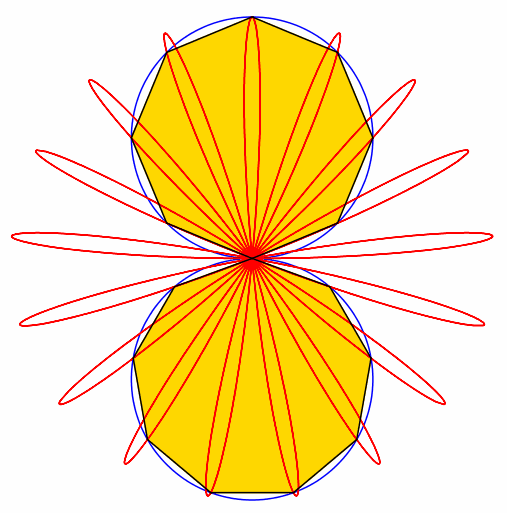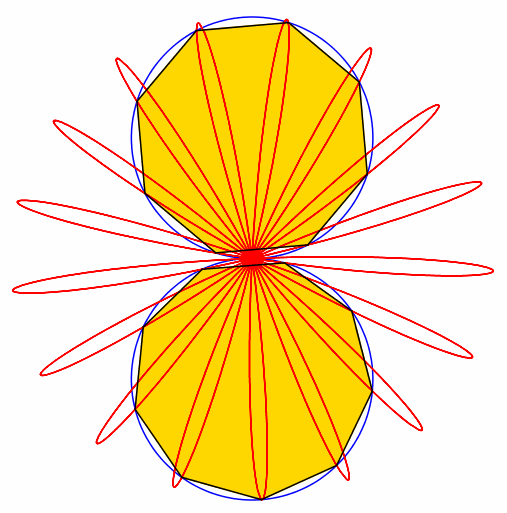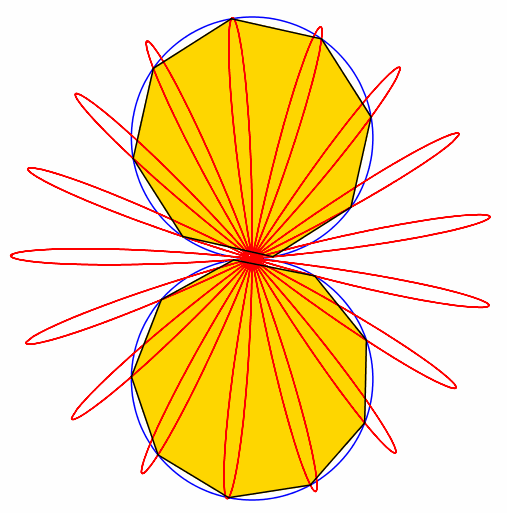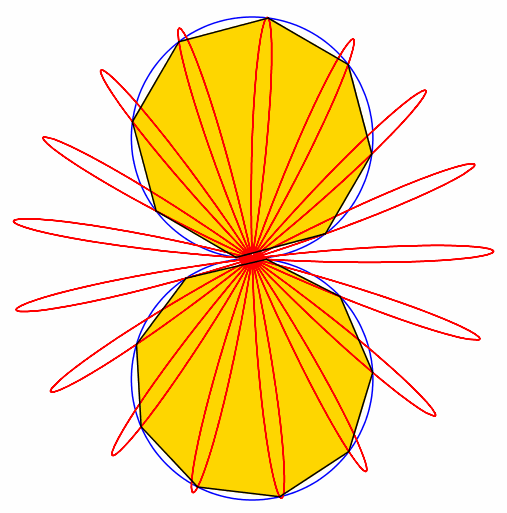
Abb. 8: 8 + 9 = 17
2 Technische Spezifikation
Das kleine regelmäßige Vieleck (oben) hat die Eckenzahl n.
Das große regelmäßige Vieleck (unten) hat die Eckenzahl (n + 1).
Die Rosette hat 2n + 1 Blätter. Ihre Parameterdarstellung ist:
Kurve(sin((2n + 1) t) cos(t + s), sin((2n + 1) t) sin(t + s), t, 0, 2π) (1)
Also:
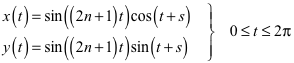 (2)
(2)
Dabei ist s der Drehparameter.
Die Drehgeschwindigkeiten der drei Figuren verhalten sich wie:
![]() (3)
(3)
Das kleine Vieleck dreht am schnellsten, die Rosette am langsamsten.
Websites
Klaus-Anton
Literatur
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1. S. 80, 89, 90.