Hans Walser, [20210709]

Rotationshyperboloid

1 Worum geht es?

Modell für das Rotationshyperboloid. Bauanleitung. Bilder und Animationen.

2 Das Modell

Das Modell ist beweglich. Im Folgenden verschiedene Situationen des Modells.

Abb. 1: Ganz schmale Situation

Abb. 2: Schmale Situation

Abb. 3: Am Äquator schneiden sich die Streifen orthogonal

Abb. 4: Breite Situation

Abb. 5: Sicht von oben

3 Bauanleitung

Das Modell besteht aus 2 mal 12 = 24 Streifen mit je sieben Löchern (Abb. 6).

Abb. 6: Ein Streifen

3.1 Papierstreifen falten

Abb. 7: Papierstreifen falten

Aus einem DIN A4-Papier können wir jeweils zwei Streifen herstellen. Wir benötigen also zwölf Blatt Papier.

Wir schneiden das Papier längs der langen Mittellinie in zwei Rechtecke. Jedes Rechteck falten wir längs drei Mal, so dass acht Lagen entstehen (Abb. 7).

3.2 Verteilung der Löcher

Abb. 8: Position der Löcher

Die Löcher sind unregelmäßig verteilt. Die Abstände zwischen den Löchern sind gegen die beiden Enden zu gespreizt (Abb. 8). Hinter dieser Unregelmäßigkeit gibt es allerdings eine versteckte Regelmäßigkeit (Abb. 9). Die Abstände ergeben sich durch einen regelmäßigen 15°-Fächer. Sie können mit der Tangens-Funktion bestimmt werden.

Abb. 9: Regelmäßiger Fächer

Der didaktische Mehrwert besteht hier in der Einsicht, dass die Tangens-Funktion nicht linear ist. Sonst gäbe es sie nicht.

3.3 Die Löcher

Die Löcher habe ich mit der Lederlochzange gestanzt. Der Lochdurchmesser richtet sich nach der Breite der für die Verbindungen verwendeten Mustertütenklammern. Für das praktische Vorgehen wird zunächst ein sorgfältig vermessener Lochstreifen hergestellt, der dann für die anderen Streifen als Markier-Lehre dient.

Insgesamt sind 24 mal 7 = 168 Löcher zu stanzen.

3.4 Zusammenbau

Der Zusammenbau ist spannend.

Wir benötigen 12 mal 7 = 84 Mustertütenklammern, halb so viele wie Löcher, da je zwei Löcher mit einer Klammer verbunden werden.

Die Streifen werden nach dem Prinzip „Lattung und Konterlattung“ verbunden und nicht nach dem Verflechtungsprinzip. Das erlaubt eine größere Beweglichkeit des Modells.

Soweit die Praxis. Und nun die Theorie.

4 Regelfläche

Das Rotationshyperboloid ist eine sogenannte Regelfläche, welche durch eine Geradenschar erzeugt wird. Im Beispiel der Abbildung 10 haben die Geraden gegenüber der Horizontalebene einen Steigungswinkel 45°. Es sind 24 Geraden der Schar gezeichnet.

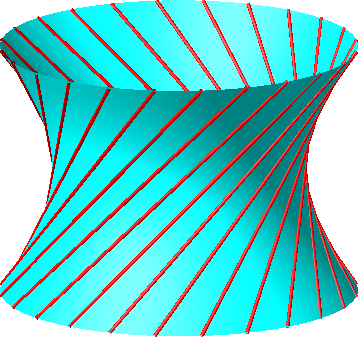
Abb. 10: Rotationshyperboloid als Regelfläche

Die Abbildung 11 gibt eine Animation dazu.

Abb. 11: Animation

Aus Symmetriegründen gibt es eine zweite Geradenschar (Abb. 12). Die Figur entspricht der Abbildung 3, allerdings nun mit doppelt so vielen Geraden.

Abb. 12: Zwei Geradenscharen

Die Abbildung 13 zeigt die Sicht von oben.

Abb. 13: Sicht von oben

Die Abbildung 14 zeigt ebenfalls die Sicht von oben, aber mit nur zwölf Geraden pro Schar. Dies entspricht unserem Modell. Zusätzlich ist der regelmäßige Fächer (Abb. 9) überlagert. Wir sehen eine gewisse Stimmigkeit. Allerdings ist zu beachten, dass die erzeugenden Geraden schräg stehen, aber alle gleich schräg. Die Teilverhältnisse der Kreuzungspunkte der Streifen bleiben also bei unserer Sicht erhalten. Der mittlere Punkt ist der Kreuzungspunkt (-Punkt) der beiden Geraden, die in unserer Sicht scheinbar aufeinander fallen. Aus den Winkelverhältnissen in der Abbildung 14 folgt die Stimmigkeit der Fächer-Überlegung.

Abb. 14: Kreuzungspunkte

In der Abbildung 15 sind auch noch Meridiane und Breitenkreise eingezeichnet. Die Meridiane sind in unserem Beispiel gleichseitige Hyperbeln, dies wegen dem Steigungswinkel 45° der erzeugenden Geradenschar. Diese Abbildung bringt keine neuen Einsichten. Sie ist lediglich schön.

Abb. 15: Meridiane und Breitenkreise

5 Veränderung des Steigungswinkels

In unserem Modell sind die Steigungswinkel der Streifen variabel. Die Abbildung 16 zeigt eine Animation dazu. Der gelbe Ring besteht aus den Brennpunkten der Hyperbeln des jeweiligen Hyperboloides. Da der Ring konstant bleibt, sind die Hyperboloide konfokal.

Abb. 16: Veränderung des Steigungswinkels. Konstanter Brennpunktkreis

Die Abbildung 17 zeigt eine Schar von fünf konfokalen Hyperboloiden, die Abbildung 18 dasselbe in einer speziellen Sicht. Wir erkennen die beiden Grenzfälle: Das in die Brennpunktkreis-Ebene plattgedrückte Hyperboloid und das zur Achse des Brennpunktkreises zusammengedrückte Hyperboloid (geschlossener Schirm). Diese beiden Grenzfälle und die dazu benachbarten Situationen sind in unserem Modell nicht realisierbar. Die Materie sträubt sich dagegen.

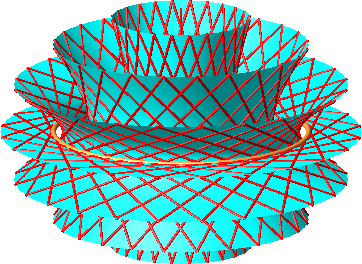
Abb. 17: Konfokale Hyperboloide

Abb. 18: Konfokale Hyperboloide. Spezielle Sicht

Die Abbildungen 19 bis 21 zeigen 51 Hyperboloide. Dabei sind die hellblauen Hyperboloid-Flächen weggelassen und nur die roten Geradenscharen gezeichnet.

Abb. 19: 51 Hyperboloid-Geradenscharen. Ansicht

Abb. 20: 51 Hyperboloid-Geradenscharen. Sicht von oben

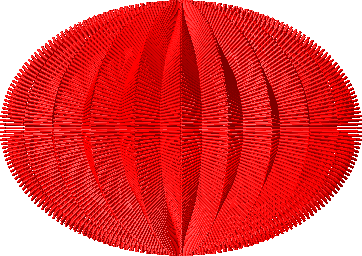
Abb. 21: 51 Hyperboloid-Geradenscharen. Sicht von vorne

Websites

Hans Walser: Rotationskörpervolumina

http://www.walser-h-m.ch/hans/Miniaturen/R/Rotationskoerpervolumina/Rotationskoerpervolumina.htm