Hans Walser, [20200217]
Regelm§ige Vielecke ungerader Eckenzahl am Dreieck
1 Worum geht es?
Spiel mit kollinearen Punkten, konstanten Teilverhltnissen und kopunktalen Geraden. Vermutungen.
2 Disposition
Es sei u = 2m – 1 eine ungerade Zahl, u ³ 5.
Einem
beliebigen Dreieck ![]() setzen wir
an den Seiten regelm§ige u-Ecke an
(Abb. 1 fr u = 7).
setzen wir
an den Seiten regelm§ige u-Ecke an
(Abb. 1 fr u = 7).
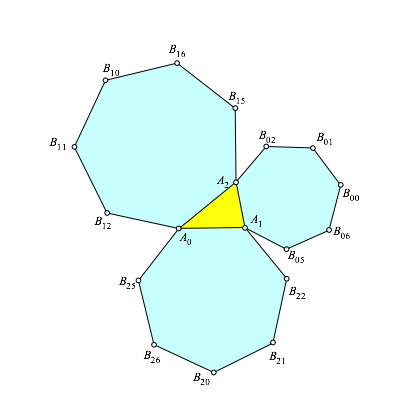
Abb. 1: Regelm§ige u-Ecke
Wir beschriften gem§ Abbildung 1. Es ist in der Zeichnung nicht eingetragen:
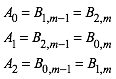 (1)
(1)
Wir
ergnzen die drei Punkte ![]() ,
, ![]() (erster
Index von B modulo 3) zum Parallelogramm
(erster
Index von B modulo 3) zum Parallelogramm
![]() (Abb. 2).
(Abb. 2).
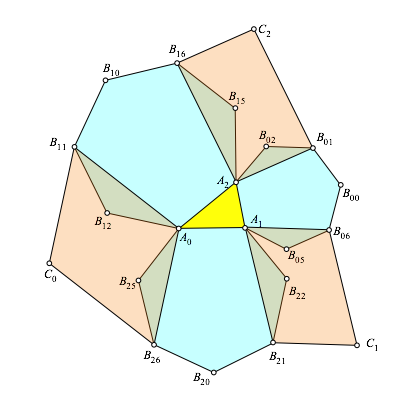
Abb. 2: Parallelogramme
3 Vermutungen
Die folgenden Vermutungen sind fr u = 5, 7, 9 und 11 mit DGS numerisch berprft.
3.1 Kollineare Punkte
Die
Punkte ![]() sind
kollinear (Abb. 3).
sind
kollinear (Abb. 3).
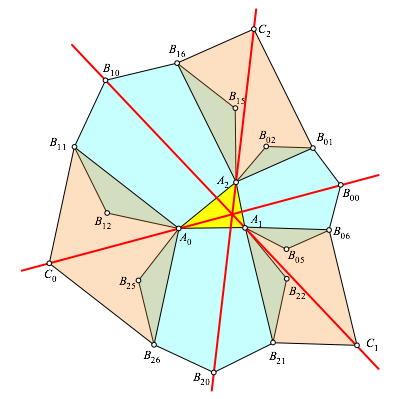
Abb. 3: Kollineare Punkte
3.2 Konstante Teilverhltnisse
![]() (2)
(2)
3.3 Diagonalenverhltnis
Dieses Teilverhltnis v ist auch das Teilverhltnis der zweitlngsten zur lngsten Diagonale im regelm§igen u-Eck und kann wir folgt formalisiert werden:
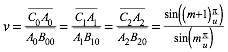 (3)
(3)
Die Tabelle 1 gibt die ersten numerischen Werte.
|
m |
u |
v |
|
3 |
5 |
0.6180339887 |
|
4 |
7 |
0.8019377357 |
|
5 |
9 |
0.8793852415 |
|
6 |
11 |
0.9189859474 |
|
7 |
13 |
0.9418836350 |
|
8 |
15 |
0.9562952016 |
|
9 |
17 |
0.9659461994 |
|
10 |
19 |
0.9727226068 |
Tab. 1: Verhltnisse
Wir erkennen beim regelm§igen Fnfeck den Goldenen Schnitt (Walser 2013). In diesem Beispiel ist die zweitlngste Diagonale die Fnfeckseite.
4 Kopunktale Geraden
Die drei
Geraden ![]() haben
einen gemeinsamen Schnittpunkt S
(Abb. 4). Dieser Schnittpunkt liegt auf der Kiepertschen Hyperbel h des Dreieckes
haben
einen gemeinsamen Schnittpunkt S
(Abb. 4). Dieser Schnittpunkt liegt auf der Kiepertschen Hyperbel h des Dreieckes ![]() . Dies folgt aus einem Satz von Jacobi (Walser 2012,
S. 153-156). Die Kiepertsche Hyperbel ist definiert durch die drei Eckpunkte
des Dreiecks, seinen Schwerpunkt und seinen Hhenschnittpunkt. Es ist eine
gleichseitige Hyperbel.
. Dies folgt aus einem Satz von Jacobi (Walser 2012,
S. 153-156). Die Kiepertsche Hyperbel ist definiert durch die drei Eckpunkte
des Dreiecks, seinen Schwerpunkt und seinen Hhenschnittpunkt. Es ist eine
gleichseitige Hyperbel.
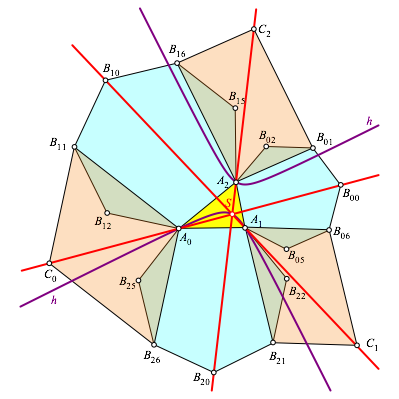
Abb. 4: Gemeinsamer Schnittpunkt
5 Weitere Vermutungen
Es gibt viele weitere Vermutungen im Umfeld unserer Figur. Wir knnen etwa gem§ Abbildung 5 Parallelogramme einfgen. Die Diagonale D0A0 verluft nun nicht mehr durch den Punkt B00. Die drei Diagonalen D0A0, D1A1 und D2A2 haben aber einen gemeinsamen Schnittpunkt T, und dieser liegt ebenfalls auf der Kiepertschen Hyperbel h (Abb. 5). Numerisch berprft.
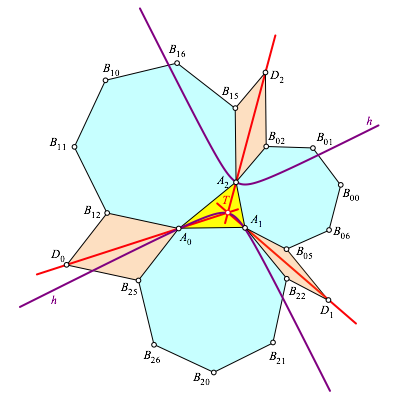
Abb. 5: Andere Parallelogramme
Beispiele dieser Art funktionieren auch mit regelm§igen Vielecken gerader Eckenzahl (Abb. 6). Numerisch berprft. Beim Schnittpunkt handelt es sich in diesem speziellen Beispiel um den Fermat-Punkt (Walser 2012, S. 155). Die roten Geraden verlaufen durch die Mittelpunkte der Sechsecke. Sie schneiden sich unter Winkeln von 60¡. Die eingezeichneten Diagonalen der Parallelogramme sind alle gleich lang und ebenso lang wie die Strecke von der Dreiecksecke zum Sechseckmittelpunkt.
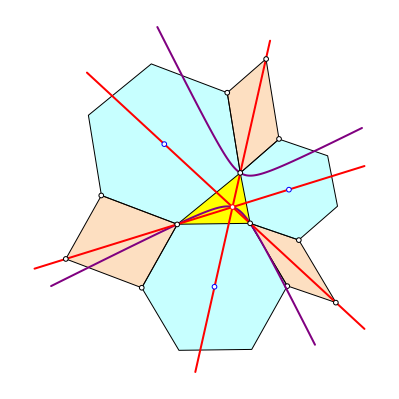
Abb. 6: Gerade Eckenzahl
Literatur
Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.
Websites
Hans Walser: Schnittpunkte
http://www.walser-h-m.ch/hans/Schnittpunkte/
Hans Walser: Schlussstriche
http://www.walser-h-m.ch/hans/Schlussstriche/