1 Worum geht es?

Zwei Halbgeraden (Abb. 1) sind mit einem S-Korbbogen zu verbinden, wobei die beiden Bögen denselben Radius haben sollen.

Konstruktionsverfahren. Mit DGS verifiziert. Beweisskizze.

Es gibt zwei Lösungen.

Abb. 1: Problemstellung

Die Abbildung 2 zeigt die Lösung.

Abb. 2: Lösung

2 Lösungsweg

Wir arbeiten mit den Bezeichnungen der Abbildung 3.

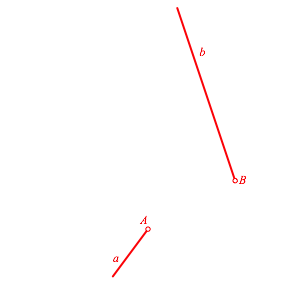
Abb. 3: Bezeichnungen

Wir zeichnen die Winkelhalbierende w der Trägergeraden von a und b (Abb. 4).

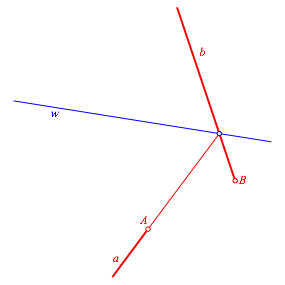
Abb. 4: Winkelhalbierende

Weiter seien M der Mittelpunkt und m die Mittelsenkrechte der Strecke AB (Abb. 5). Die Mittelsenkrechte m schneiden wir mit der Winkelhalbierenden w in N. Um N zeichnen wir den Kreis k durch A und B.

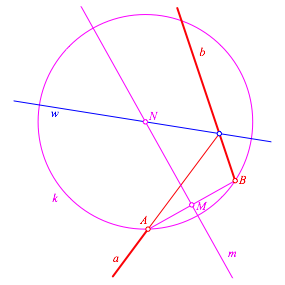
Abb. 5: Mittelsenkrechte und Kreis

Durch M zeichnen wir das Lot l zu w und schneiden mit dem Kreis k. Dies liefert den Übergangspunkt Ü (Abb. 6).

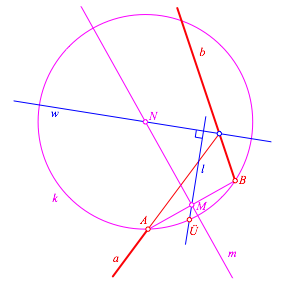
Abb. 6: Übergangspunkt

Die Zentren der Korbbögen finden wir mit Senkrechten und Mittelsenkrechten gemäß Abbildung 7.

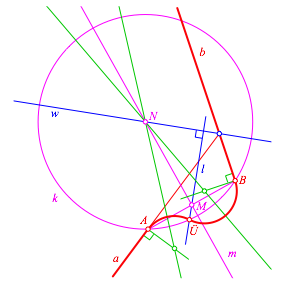
Abb. 7: Konstruktion der Korbbögen

3 Beweisskizze

Der Trick ist natürlich die etwas mysteriöse Konstruktion des Übergangspunktes Ü. Man beachte, dass das Lot l parallel ist zur zweiten Winkelhalbierenden der Trägergeraden von a und b.

3.1 Übergangspunkt

Zunächst folgt aus der allgemeinen Theorie der Korbbögen, dass der Übergangspunkt Ü auf dem Kreis k liegen muss (vgl. [1] ). Bei einer beliebigen Wahl des Übergangspunktes auf dem Kreis k haben die beiden Korbbögen nicht den gleichen Radius. Für Ü = A hat der bei A beginnende Bogen den Radius null und der andere Bogen einen positiven Radius, für Ü = B ist es umgekehrt. Da sich die Radien bei Variation des Punktes Ü auf dem Bogen AB monoton verändern, gibt es genau eine Stelle mit gleich großen Radien.

3.2 Zickzacklinie

Für die gleichen Radien ergibt sich eine Zickzacklinie (schwarz in Abb. 8) von A nach B, deren Knoten auf den grünen Normalen liegen und deren Mittelstück doppelt so lang ist wie die Endstücke. Der Mittelpunkt ist dann der Übergangspunkt Ü.

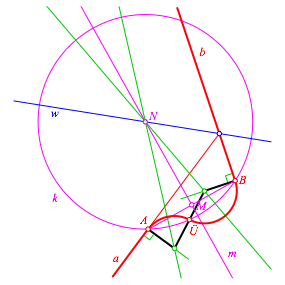
Abb. 8: Zickzacklinie

3.3 Ortslinie

Wir variieren die Zickzacklinie wie folgt (Abb. 9). Zu einem Parameter t wählen wir auf den beiden grünen Normalen je einen Knotenpunkt im Abstand t von A beziehungsweise B. Wir verbinden diese beiden Knotenpunkte. So entsteht eine Zickzacklinie, deren Mittelstück im Allgemeinen nicht doppelt so lang ist wie die beiden Endstücke. Wir fragen nach der Ortslinie des Mittelpunktes P des Mittelstückes bei Variation des Parameters t. Auf dieser Ortslinie liegt auch der Übergangspunkt Ü.

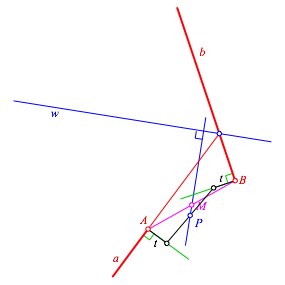
Abb. 9: Variation der Zickzacklinie

In einer vektoriellen Notation sieht man, dass die Sache linear ist. Die Ortslinie ist eine Gerade. Ihr Richtungsvektor ist das arithmetische Mittel der Einheitsrichtungsvektoren der beiden grünen Normalen und damit parallel zur Winkelhalbierenden dieser grünen Normalen und weiter orthogonal zu w. Schließlich erhalten wir für t = 0 den Punkt M. Die Ortslinie ist also das Lot l (Abb. 6).

Damit ist der Übergangspunkt Ü der Schnittpunkt des Lotes l mit dem Kreis k. Dies war zu beweisen.

4 Zweite Lösung

Der zweite Schnittpunkt des Lotes l mit dem Kreis k liefert analog die zweite Lösung (Abb. 10).

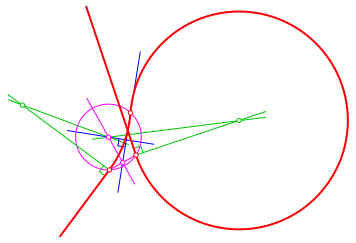
Abb. 10: Zweite Lösung

Websites

[1] Frank Rolfdieter und Walser Hans: Korbbögen – wie kriegen wir die Kurve?

http://www.walser-h-m.ch/hans/Miniaturen/K/Korbboegen/Korbboegen.pdf