Hans Walser, [20200214]
S-Korbbogen
Idee und Anregung: Anton Gfrerrer, Graz
1 Worum geht es?
Zwei Halbgeraden (Abb. 1) sind mit einem S-Korbbogen zu verbinden, wobei die beiden Bgen denselben Radius haben sollen.
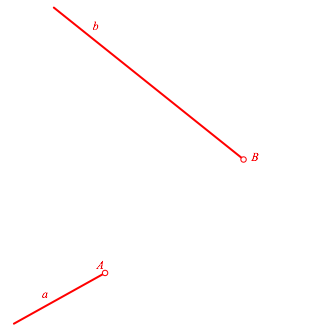
Abb. 1: Problemstellung
Die Abbildung 2 zeigt eine der beiden Lsungen.
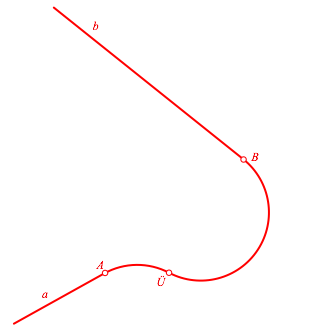
Abb. 2: Lsung
2 Schubspiegelung
Die Bedingung der gleichen Radien der beiden Korbbgen gehen wir mit Symmetrien an. Zunchst arbeiten wir mit einer Schubspiegelung (Abb. 3). Diese soll den Punkt A auf den Punkt B abbilden und die Halbgerade a auf die zur Halbgeraden b komplementre Halbgerade. Die Achse l dieser Schubspiegelung verluft durch den Mittelpunkt M der Strecke AB. Ihre Richtung ergibt sich durch Winkelhalbierende von a und b. Die Strecke PQ ist die Schublnge. Wir brauchen im Folgenden die halbe Schublnge, in der Abbildung 3 fett eingezeichnet.
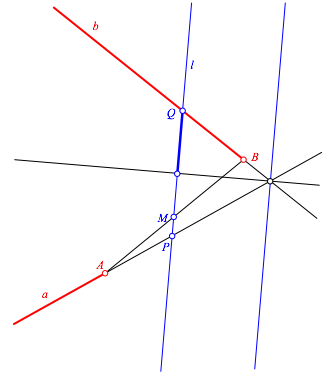
Abb. 3: Schubspiegelung
Im Folgenden werden die Details der Konstruktion der Schubspiegelelemente nicht mehr angegeben.
3 Nchste Konstruktionsschritte
Wir zeichnen in B die Normale n zu b und damit ein rechtwinkliges Dreieck (gelb in Abb. 4) mit der Strecke QB als der einen Kathete und der halben Schublnge als der anderen Kathete. Die Hypotenusenlnge verwenden wir als Radius eines Kreises um Q. Diesen Kreis schneiden wir mit l in S1 und S2. Wir arbeiten im Folgenden mit S1 weiter. Die aus S2 sich ergebende zweite Lsung wird unten angegeben.
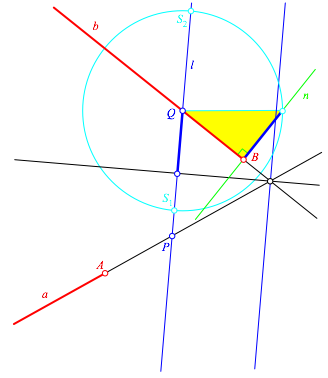
Abb. 4: Normale. Rechtwinkliges Dreieck. Kreis
Wir schneiden die Normale zu l in S1 mit der Geraden n (Abb. 5). Der Schnittpunkt Nb ist das Zentrum des Trgerkreises des von B ausgehenden Korbbogens. Er verluft bis zum Schnittpunkt mit l.
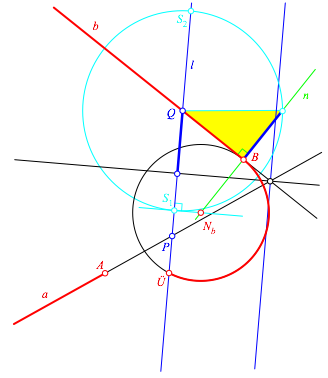
Abb. 5: Der eine der beiden Kreisbgen
Punktspiegelung an liefert den Trgerkreis des anderen Bogens (Abb. 6).
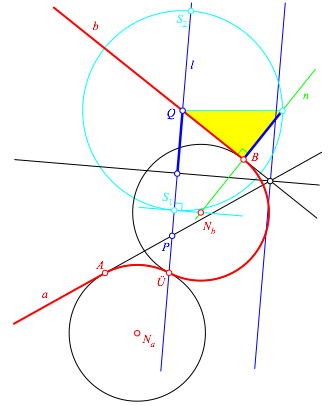
Abb. 6: Der andere Korbbogen
4 Hintergrund
Wir bilden die Halbgerade a und den von A ausgehenden Korbbogen mit unserer Schubspiegelung ab (magenta in Abb. 7). Der schubgespiegelte Korbbogen und der von B ausgehende Korbbogen liegen additiv auf demselben Kreis, der aber noch eine Lcke offen hat. Die Sehne dieser Lcke, also die Strecke Õ, hat die Schublnge der Schubspiegelung.
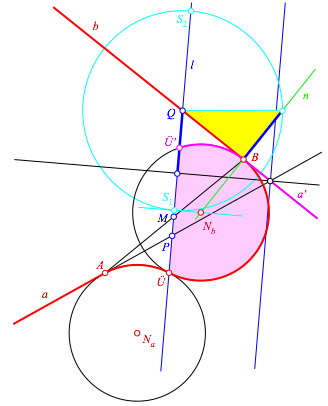
Abb. 7: Schubspiegelung
Aus dem Potenzsatz (Potenz des Punktes Q bezglich des Kreises mit der Lcke) ergibt sich die Stimmigkeit unserer Konstruktion.
5 Zweite Lsung
Der Punkt S2 fhrt analog zur zweiten Lsung (Abb. 8).
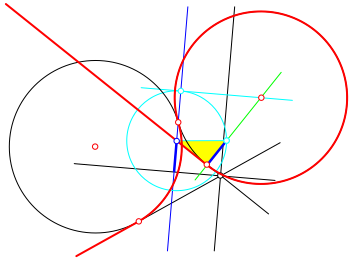
Abb. 8: Zweite Lsung
Die Abbildung 9 zeigt die berlagerung der beiden Lsungen.
Man kann die Figur fr einen Spurwechsel von Rechtsverkehr auf Linksverkehr benutzen. Allerdings sind Korbbgen wegen der abrupten Krmmungsnderung an den bergangspunkten fr Verkehrstrassen nicht geeignet.

Abb. 9: Beide Lsungen
Websites
[1] Frank Rolfdieter und Walser Hans: Korbbgen – wie kriegen wir die Kurve?
http://www.walser-h-m.ch/hans/Miniaturen/K/Korbboegen/Korbboegen.pdf
[2] Hans Walser: S-Korbbogen
http://www.walser-h-m.ch/hans/Miniaturen/S/S-Korbbogen/S-Korbbogen.htm