Hans Walser, [20150924]
Sangaku
1 Worum geht es
Es wird ein Beispiel eines Sangakus besprochen (Abb. 1).
Sangku sind geometrische Figuren aus japanischen Tempeln, welche Geometrie-Probleme ohne Worte zeigen.

Abb. 1: Sangaku. Rot gleich blau
Da die Aufgabenstellung fehlt, kšnnen wir uns selber eine ausdenken.
Zum Beispiel: Die gesamte rote FlŠche ist gleich gro§ wie die gesamte blaue FlŠche. Kurz: Rot gleich blau. Das kann rechnerisch mit dem Kosinussatz bewiesen werden.
Die Figur hat aber viele weitere Eigenschaften.
2 Hšhen und Seitenhalbierende
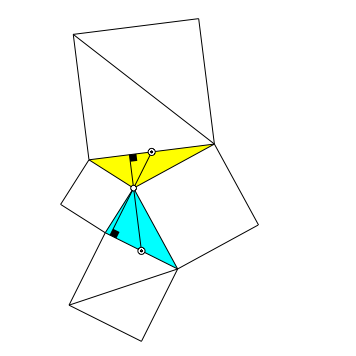
Abb. 2: Hšhen und Seitenhalbierende
Die beiden Dreiecke im Zentrum der Figur haben eine Ecke gemeinsam. Die Hšhe des einen Dreiecks durch diese gemeinsame Ecke liegt auf derselben Geraden wie die Seitenhalbierende des anderen Dreiecks.
3 Viereck mit orthogonalen Diagonalen
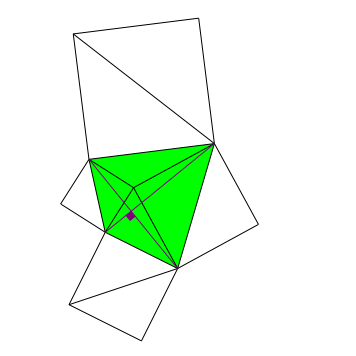
Abb. 3: Orthogonale Diagonalen
Im markierten Viereck haben wir orthogonale Diagonalen.
4 Rechtwinklig gleichschenklige Dreiecke

Abb. 4: Rechtwinklig gleichschenklige Dreiecke
Wir kšnnen zwei rechtwinklig gleichschenklige Dreiecke einpassen. Diese haben die Spitze gemeinsam.
5 Ein rechtwinkliges Dreieck

Abb. 5: Rechtwinkliges Dreieck
In die †berlagerung der Abbildungen 3 und 4 kšnnen wir ein rechtwinkliges Dreieck einpassen. Es hat den rechten Winkel im Schnittpunkt der beiden orthogonalen Diagonalen.
6 Symmetrie

Abb. 6: Symmetrie
Das Originalbeispiel der Abbildung 1 ermangelt jeder Symmetrie. Die Abbildung 6 zeigt eine bessere Version.
7 Neues Arrangement
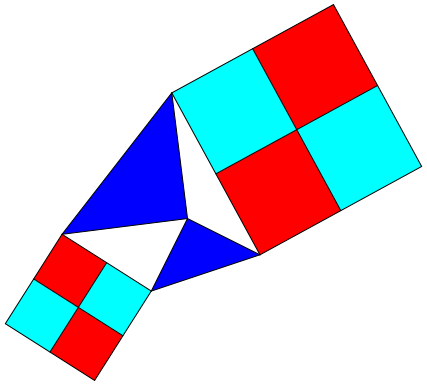
Abb. 7: Neues Arrangement
Wir kšnnen die Bauteile der Abbildung 6 durch Verschieben neu arrangieren. Da sehen wir, was Symmetrie vermag.
8 Symmetrie
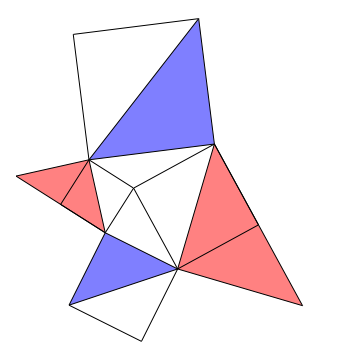
Abb. 8: Rot gleich blau
Wir haben vier rechtwinklig gleichschenklige Dreiecke.
9 Angesetzte Quadrate
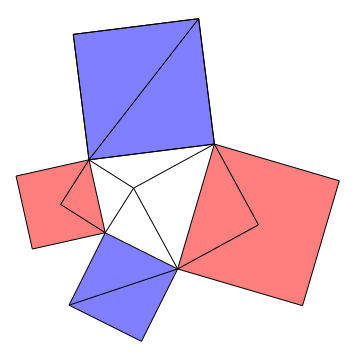
Abb. 9: Rot gleich blau
Die Abbildung 9 erinnert an den Satz des Pythagoras und soll dies auch.
10 †berlappende Quadrate
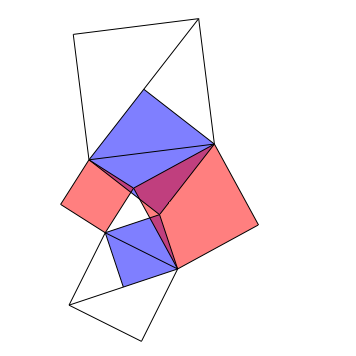
Abb. 10: Rot gleich blau
11 Kreise
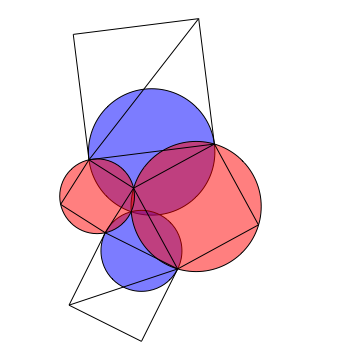
Abb. 11: Rot gleich blau
Die vier Thaleskreise haben einen Punkt gemeinsam.