Hans Walser, [20150101]
Schachbrett-Geometrie
1 Worum es geht
Auf dem Schachbrett wird eine Metrik definiert, die sich an den Bewegungen von Schachfiguren orientiert. Fźr eine bestimmte Schachfigur ist der Abstand zwischen zwei Feldern des Schachbrettes die minimale Anzahl Zźge, um mit dieser Figur von einem Feld zum andern zu gelangen.
ZusŠtzlich studieren wir die Anzahl der Wege minimaler LŠnge von einem Feld zum anderen.
2 Beispiele
In den Beispielen werden die AbstŠnde gemŠ§ Tabelle 1 farblich codiert.
|
Abstand |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Farbe |
schwarz |
rot |
grźn |
gelb |
blau |
magenta |
zyan |
|
|
|
|
|
|
|
|
Tab. 1: Farbcodierung
2.1 Bauern
Da die Bauern nicht rźckwŠrts ziehen kšnnen, ergibt sich eine asymmetrische Metrik. Zudem kann auf einem leeren Schachbrett ein Bauer nur geradeaus ziehen. Er kann nicht jedes Feld erreichen.
Daher lassen wir die Bauern aus unseren †berlegungen weg.
2.2 Turm
2.2.1 †blicher Turm
Die Felder in der gleichen Spalte oder in der gleichen Zeile wie das Ausgangsfeld haben davon den Abstand 1, und es gibt nur einen Minimalweg dazu. Diese Felder sind in der Abbildung 1 rot markiert.
Alle źbrigen Felder haben den Abstand 2, und es gibt genau zwei Minimalwege dazu. Diese Felder sind in der Abbildung 1 grźn markiert.
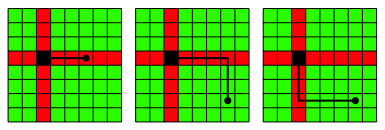
Abb. 1: Situation fźr einen Turm
Das ist nicht besonders spannend. Wir Šndern daher die Regeln fźr den Turm leicht ab.
2.2.2 Einschrittiger Turm
De Turm soll nur senkrecht oder waagerecht ins Nachbarfeld ziehen kšnnen. Die Abbildung 2 zeigt die jeweils in gleicher Farbe die Felder, welche vom zentralen schwarzen Feld denselben Abstand haben. Diese ăKreiseŇ sind spitzstŠndige Quadrate.
Aus Šsthetischen Grźnden wurde das Schachbrett grš§enmŠ§ig dem Problem angepasst.
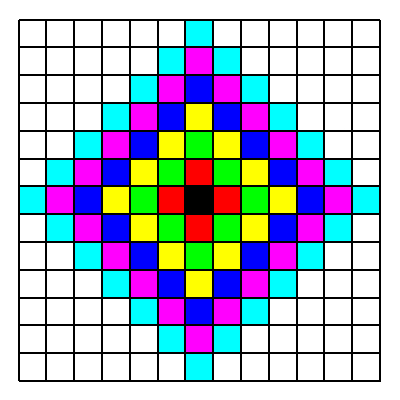
Abb. 2: AbstŠnde fźr einen einschrittigen Turm
In der Abbildung 3 sind die Anzahlen der Minimalwege eingetragen, welche vom Zentrum aus zu den jeweiligen Feldern fźhren. Wir erkennen die Binomialkoeffizienten.

Abb. 3: Anzahl Wege fźr den einschrittigen Turm
2.3 LŠufer
2.3.1 †blicher LŠufer
Fźr einen LŠufer (Abb. 4) ist die Situation im Prinzip gleich wie fźr einen Turm, nur eben diagonal. Zudem sind ihm nur die HŠlfte der Felder zugŠnglich.
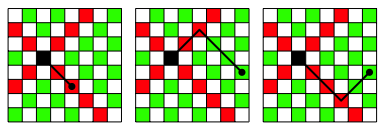
Abb. 4: Situation fźr den LŠufer
2.3.2 Einschrittiger LŠufer
Die Abbildung 5 zeigt die Abstandssituation fźr einen einschrittigen LŠufer. Die ăKreiseŇ sind jetzt bodenstŠndige Quadrate.
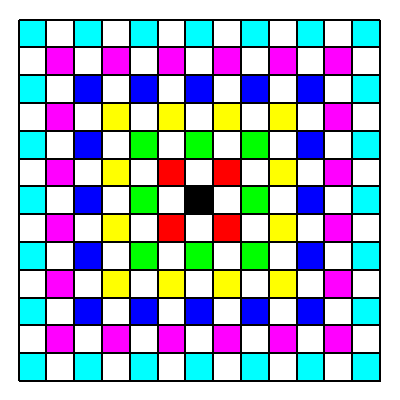
Abb. 5: AbstŠnde fźr einen einschrittigen LŠufer
Die Abbildung 6 zeigt die Anzahlen der Minimalwege. Es ergeben sich wiederum die Binomialkoeffizienten.

Abb. 6: Anzahl Wege fźr den einschrittigen LŠufer
2.4 Dame
Die Abbildung 7 zeigt die Farbcodierung der AbstŠnde fźr die Dame.
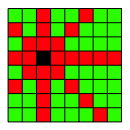
Abb. 7: AbstŠnde fźr die Dame
Felder mit dem Abstand 2, welche bezźglich des Schachbrettes dieselbe Farbe haben, lassen bis zu 12 Wege zu (Abb. 8).
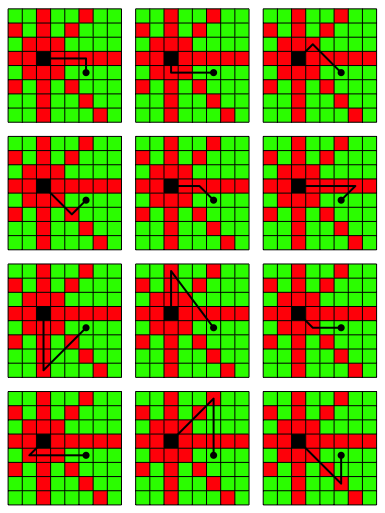
Abb. 8: Es fźhren viele Wege nach Rom
2.5 Kšnig
Der Kšnig ist eine einschrittige Dame. Die Abbildung 9 zeigt die Distanzen. Die ăKreiseŇ sind bodenstŠndige Quadrate.
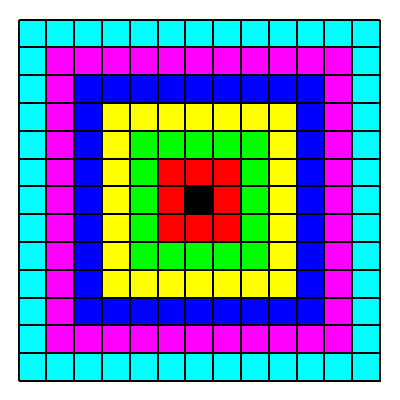
Abb. 9: AbstŠnde fźr den Kšnig
Fźr die Anzahl der Minimalwege erhalten wir die Daten der Abbildung 10.
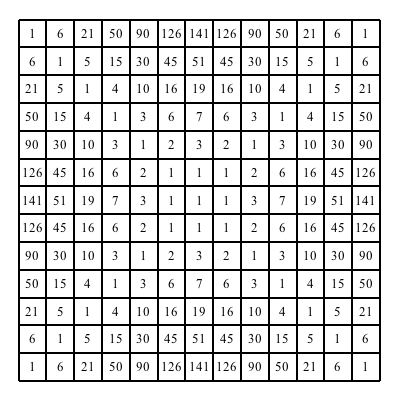
Abb. 10: Anzahl Wege fźr den Kšnig
Es handelt sich beim Zahlendreieck von der Mitte aus nach unten um die Trinomialkoeffizienten in folgender Schreibweise:
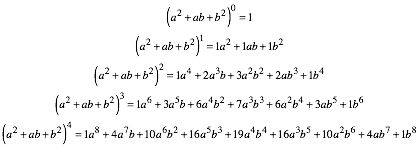
Eine alternative Schreibweise geht mit Polynomen in x (siehe[1]):
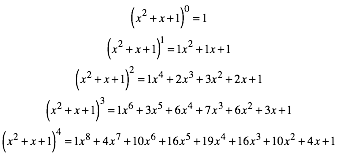
2.6 Springer
Fźr einen Springer ergeben sind die AbstŠnde gemŠ§ Abbildung 11.

Abb. 11: AbstŠnde fźr den Springer
Wir sehen, dass die ăMonotonieŇ gestšrt ist. Die Felder unmittelbar neben dem Ursprungsfeld (im Sinne der źblichen Metrik) haben von diesem den Abstand 3.
Die Abbildung 12 zeigt die Situation nur bis zum Abstand 4.
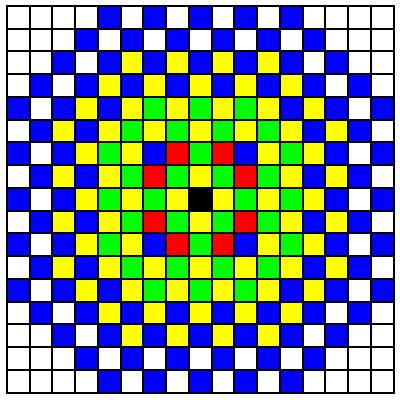
Abb. 12: AbstŠnde bis 4 fźr den Springer
Auch fźr die Anzahl Wege wird es dramatisch (Abb. 13, ebenfalls nur bis Abstand 4).

Abb. 13: Anzahl Wege fźr den Springer
Wir erkennen zwar am Šu§ersten Rand die Binomialkoeffizienten. Auch im Innern kann man sie in einer Ršsselsprung-Disposition finden.
Die Abbildung 14 zeigt eine †berlagerung der Abbildungen 12 und 13.
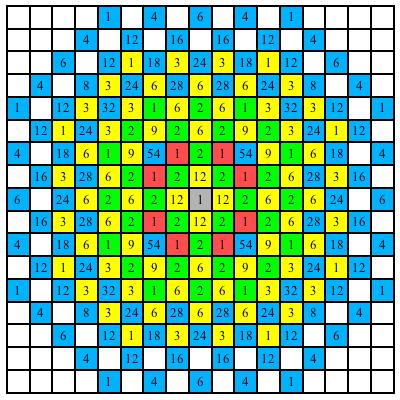
Abb. 14: Abstand farbcodiert, Anzahl Wege als Zahl, fźr den Springer
Die Abbildung 15 zeigt einen Ausschnitt rechts oben. Darin ist blau der Kreis eingezeichnet, der genau durch diejenigen gelben Felder geht, von denen aus das in der Abbildung 15 zentrale blaue Feld mit einem Ršsselsprung erreicht werden kann. Diese gelben Felder haben vom Ursprungsfeld den Abstand 3, das blaue Feld also den Abstand 4.
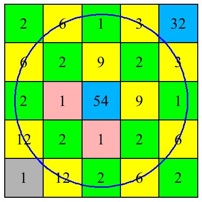
Abb. 15: Ausschnitt
Die Wege zum blauen Feld laufen źber eines dieser gelben Felder. Fźr die Anzahl der Wege vom Ursprung zum blauen Feld erhalten wir also die Summe der Weganzahlen zu den gelben Feldern. Das ist:
![]()
Der blaue
Kreis hat den Radius ![]() . Das schmeckt nach dem Goldenen Schnitt. TatsŠchlich
finden wir den Goldenen Schnitt etwa gemŠ§ Abbildung 16, und zwar in der
Reihenfolge Minor-Major-Minor.
. Das schmeckt nach dem Goldenen Schnitt. TatsŠchlich
finden wir den Goldenen Schnitt etwa gemŠ§ Abbildung 16, und zwar in der
Reihenfolge Minor-Major-Minor.
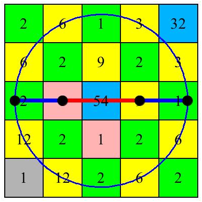
Abb. 16: Goldener Schnitt
Websites
[1] https://oeis.org