Hans Walser, [20220808]
Schachbrett
1 Worum geht es?
Die Quadratfelder eines Schachbrettes werden mit Viertelkreisen garniert. Schöne Figuren.
2 Viertelkreise
Wir zeichnen in das Quadratfeld zwei Viertelkreise (Abb. 1). Die Zentren sind diametrale Quadratecken, der Radius die halbe Quadratseite.

Abb. 1: Viertelkreise
Die Viertelkreise benachbarter Quadratfelder gehen bündig ineinander über (Abb. 2).

Abb. 2: Bündiger Übergang
3 Vierteldrehung
Wir können einzelne Quadratfelder um 90° drehen (Abb. 3). Der Übergang bleibt bündig.

Abb. 3: Drehung eines Quadratfeldes
4 Standard-Schachbrett
In den folgenden Überlegungen gehen wir jeweils vom Standard-Schachbrett der Abbildung 4 aus. Wir sehen Wellenlinien, die von links oben nach rechts unten verlaufen.

Abb. 4: Standard-Schachbrett
5 Verdrehungen
In der Abbildung 5 ist ein einziges Quadratfeld verdreht. Wir sehen sofort, welches.

Abb. 5: Ein Quadratfeld ist verdreht
Werden alle gelben Quadratfelder verdreht, ergeben sich kleine Kreise (Abb. 6).

Abb. 6: Kreise
Dasselbe geschieht, wenn alle blauen Quadratfelder verdreht werden (Abb. 7). Die Kreise sind aber anders positioniert.

Abb. 7: Anders positionierte Kreise
Werden überhaupt alle Quadratfelder verdreht, ergeben sich Wellenlinien von links unten nach rechts oben (Abb. 8).

Abb. 8: Alle Quadratfelder verdreht
Die Abbildung 9 zeigt ein systematisches Verdrehen der Quadratfelder und damit den Übergang von der Abbildung 4 zur Abbildung 8 und zurück. Die Verdrehungs-Reihenfolge ist spaltenweise, links unten beginnend.

Abb. 9: Systematisches Verdrehen
6 Diagonalen
In der Abbildung 10 sind die gelben Quadratfelder in der Diagonalen von links oben nach rechts unten verdreht.

Abb. 10: Kreise in der Diagonalen
In der Abbildung 11 sind dagegen die blauen Quadratfelder in der Diagonalen von links unten nach rechts oben verdreht.

Abb. 11: Andere Diagonale
Schließlich die Verdrehung in beiden Diagonalen (Abb. 12).

Abb. 12: Beide Diagonalen
7 Transformation in sich selber
Die Abbildung 13 zeigt eine Transformation der Abbildung 4 in sich selber.
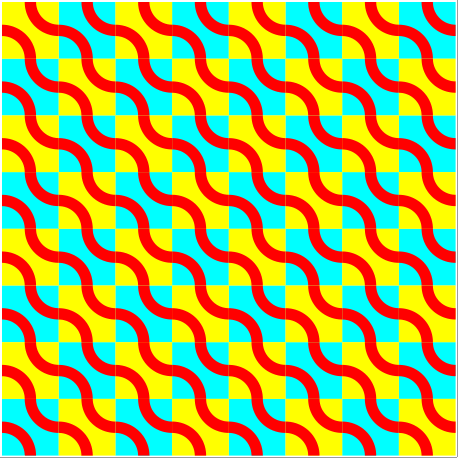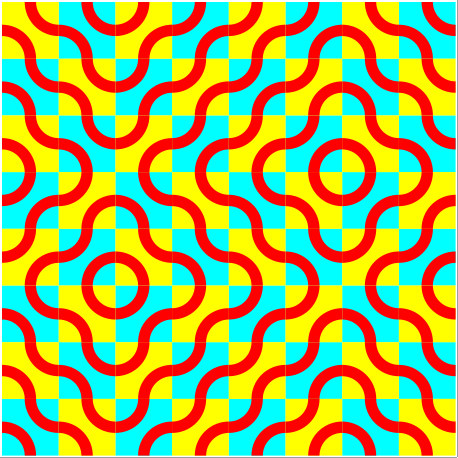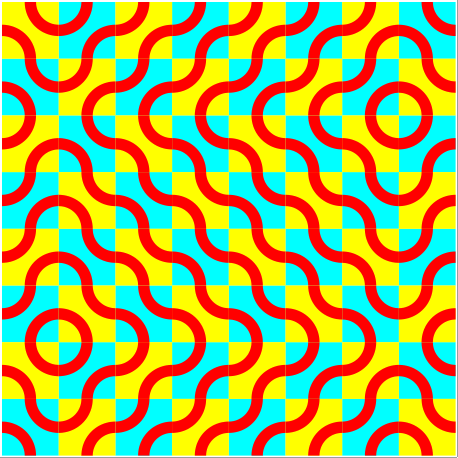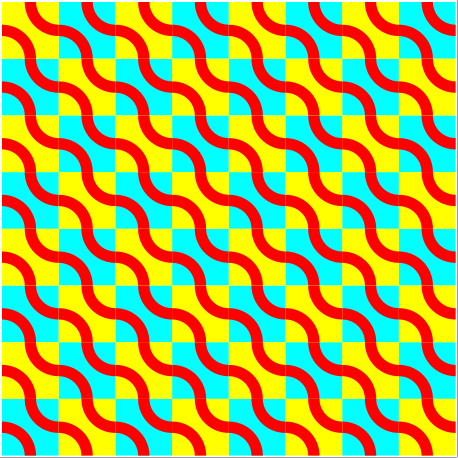
Abb. 13: Transformation in sich selber
8 Jedes dritte Quadratfeld
In der Abbildung 14 wird spaltenweise, links unten beginnend, jedes dritte Quadratfeld verdreht.

Abb. 14: Jedes dritte kommt dran
9 Primzahlen
In der Abbildung 15 wird spaltenweise, links unten mit null beginnend, jedes Quadratfeld mit einer Primzahlnummer verdreht.

Abb. 15: Alle Primzahlen kommen dran
10 Münzenwurf
In der Abbildung 16 wird mit dem Zufallsgenerator gefuhrwerkt.

Abb. 16: Kopf oder Zahl?
Weblinks
Hans Walser: Deformiertes Sechseck
http://www.walser-h-m.ch/hans/Miniaturen/D/Deformiertes_Sechseck/Deformiertes_Sechseck.html
Hans Walser: Hexagon
http://www.walser-h-m.ch/hans/Miniaturen/H/Hexagon/Hexagon.html