1 Worum geht es?

Eine fehlerhafte Handhabung der Brennpunkt-Leitgerade-Definition der Parabel führt zu einer Hyperbel.

2 Erinnerung

Die Menge der Punkte P, welche vom Brennpunkt F und der Leitgeraden l denselben Abstand haben, ist eine Parabel (Abb. 1).

Abb. 1: Parabel

Der Abstand des Punktes P von der Leitgeraden l wird senkrecht (rechtwinklig) gemessen.

3 Schiefe Messung

Wir messen nun den Abstand des Punktes P von der Leitgeraden schief, das heißt unter einem vom rechten Winkel verschiedenen Winkel ϕ. In der Abbildung 2 wurde der Winkel ϕ = 30° gewählt. Die Strecken CP sind alle parallel.

Abb. 2: Schiefe Messung

Wir vermuten, dass die Menge der Punkte P eine Hyperbel ist.

Die Situation kann auch mit einem gleichschenkligen Dreieck dargestellt werden (Abb. 3). Die Schenkellänge ist gleich der Länge der Strecke FP.

Abb. 3: Gleichschenkliges Dreieck

Der Abstand des Punktes P von der Leitlinie l ist die Höhe dieses Dreiecks. Diese Höhe ist gegenüber der Schenkellänge verkürzt. Der Verkürzungsfaktor ist sin(ϕ), in unserem Beispiel also ½.

4 Nachweis der Hyperbel

Wir arbeiten mit den Bezeichnungen im kartesischen Koordinatensystem der Abbildung 4.

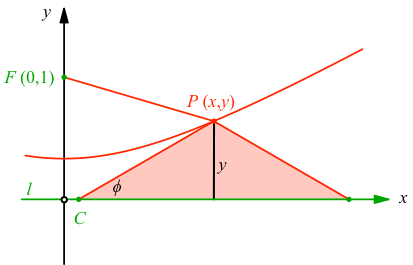
Abb. 4: Maße und Bezeichnungen

Es ist:

Weiter ist:

Somit haben wir für die gesuchten Punkte P die Bedingung:

Wir schreiben das in der allgemeinen Form:

Dies kann umgeformt werden zu:

Für a² > 1 ist dies die Gleichung einer Ellipse.

Für a² < 1 ist dies die Gleichung einer Hyperbel. Dies ist unser Fall.

Für a² = 1 fällt der Term mit y² weg und die Gleichung kann umgeformt werden zu:

Dies ist die Gleichung einer Parabel.

5 Konstruktion

Mit zwei eingepassten Rhomben (blau in Abb. 5) können die Scheitelpunkte der Hyperbel konstruiert werden. Zusammen mit dem Brennpunkt F sind nun ausreichend Informationen für die Hyperbel vorhanden.

Abb. 5: Konstruktion