Hans Walser, [20150928]
Schiefer Pythagoras
1 Worum geht es?
Es wird eine Variation des Satzes des Pythagoras bearbeitet, welche nicht auf das rechtwinklige Dreieck beschrnkt ist.
2 Der klassische Satz des Pythagoras
Die Abbildung 1 illustriert den klassischen Satz des Pythagoras.
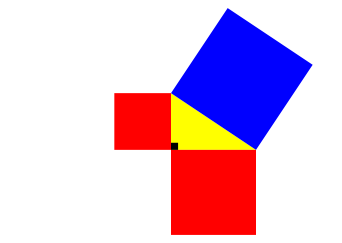
Abb. 1: Blau = rot
Der rechte Winkel des gelben Dreiecks ist wesentlich. Wir der rechte Winkel zum Beispiel durch einen spitzen Winkel ersetzt, verkleinert sich das blaue Quadrat (Abb. 2).

Abb. 2: Blau < rot
3 Der doppelte Pythagoras
3.1 Symmetrische Figur
Wir knnen die Figur der Abbildung 1 erweitern (Abb. 3). Somit erhalten wir eine achsensymmetrische Figur.
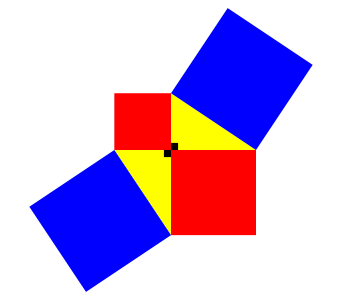
Abb. 3: Blau = 2 mal rot
3.2 Asymmetrische Figur
Wenn wir in der Figur der Abbildung 3 den rechten Winkel verndern, bleibt die Gleichheit erhalten (Abb. 4).
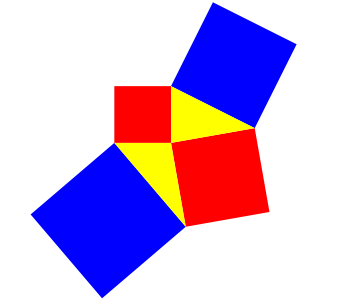
Abb. 4: Blau = 2 mal rot
Das eine blaue Quadrat wird kleiner, das andere aber flchenm§ig um gleich viel gr§er.
3.3 Iteration
Wir verschieben die beiden blauen Quadrate der Abbildung 4 gem§ Abbildung 5. Dann knnen wir die ursprnglichen roten Quadrate je viermal ansetzen, auch hier ausschlie§lich mit Verschiebungen in die Endlage gebracht.

Abb. 5: Iteration
3.4 Beweis fr den doppelten Pythagoras
Fr den rechnerischen Beweis mit dem Kosinussatz verwenden wir die Bezeichnungen der Abbildung 6.

Abb. 6: Bezeichnungen
Nach dem Kosinussatz ist:
![]() (1)
(1)
![]() (2)
(2)
Wegen ![]() sind die
beiden Kosinuswerte entgegengesetzt gleich. Addition von (1) und (2) liefert
daher:
sind die
beiden Kosinuswerte entgegengesetzt gleich. Addition von (1) und (2) liefert
daher:
![]() (3)
(3)
3.5
3.6 Ganzzahliges Beispiel
Wegen
![]() (4)
(4)
ist bei gegebenen ganzzahligen Werten fr a, b, c der Wert d in der Regel nicht ganzzahlig. Es gibt aber ganzzahlige (ãpythagoreischeÒ) Lsungen, etwa a = 9, b = 7, c = 8 und d = 14. Die Abbildung 7 zeigt die Figur mit einem Zerlegungsbeweis fr (3).

Abb. 7: Ganzzahliges Beispiel
4 Die beiden Dreiecke
Die beiden rechtwinkligen Dreiecke der Figur der Abbildung 3 sind kongruent.
Die beiden Dreiecke der Figur der Abbildung 4 sind nicht kongruent. Das eine ist spitzwinklig, das andere stumpfwinklig. Trotzdem haben sie Gemeinsamkeiten.
4.1 Flchengleichheit
Die beiden Dreiecke sind flchengleich.
4.1.1 Rechnerischer Beweis
Mit den Bezeichnungen der Abbildung 6 erhalten wir fr die beiden Dreiecke die Flcheninhalte:
![]() (5)
(5)
Wegen ![]() sind die
beiden Sinuswerte gleich.
sind die
beiden Sinuswerte gleich.
4.1.2 Zerlegungsbeweis
Die Abbildung 8 zeigt einen Zerlegungsbeweis.
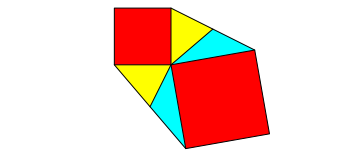
Abb. 8: Zerlegungsbeweis
4.1.3 Ergnzungsbeweis
Wir knnen die beiden Dreiecke durch Punktspiegelung je zu einem Parallelogramm ergnzen (Abb. 9). Die beiden Parallelogramme sind kongruent und um 90¡ relativ zueinander verdreht.
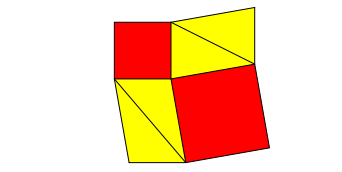
Abb. 9: Ergnzungsbeweis
Die roten Quadrate und die gelben Parallelogramme knnen zu einer Parkettierung erweitert werden (Abb. 10).

Abb. 10: Parkettierung
4.2
4.3 Hhen und Seitenhalbierende
Die beiden gelben Dreiecke haben einen Punkt gemeinsam. Die Hhe des einen Dreiecks durch diesen Punkt liegt auf derselben Geraden wie die Seitenhalbierende des anderen Dreiecks (Abb. 11).
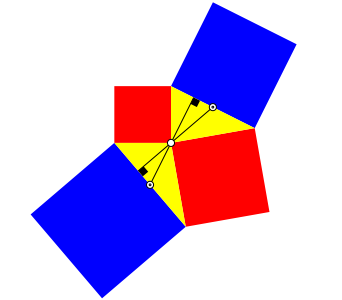
Abb. 11: Hhen und Seitenhalbierende
Der Beweis ergibt sich aus der Ergnzung der Dreiecke zum Parallelogramm gem§ Abbildung 9. Die Parallelogramme sind um 90¡ verdreht. Wenn wir noch je die zweite Diagonale einzeichnen, wird alles klar (Abb. 12).
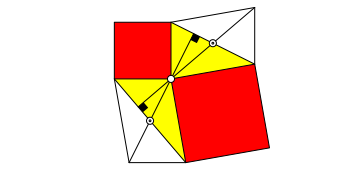
Abb. 12: Beweis
5 Entfernung des Faktors 2
Die Bildlegende der Abbildung 4 und die entsprechende Gleichung (3) enthalten den Faktor 2, der als sthetische Strung empfunden werden kann.
Wir knnen ihn loswerden, indem wir die blauen Quadrate halbieren (Abb. 13).
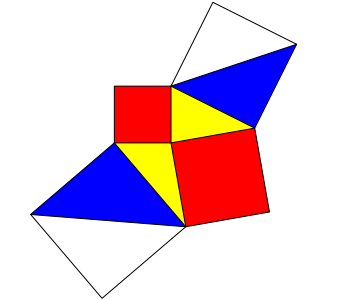
Abb. 13: Blau = rot
Nun sind wir den Faktor 2 los, dafr haben wir einerseits rote Quadrate und andererseits blaue rechtwinklig gleichschenklige Dreiecke.
Der Autor hat diese Figur als Sangaku in Bonn gesehen. Sie war der Auslser zu den vorliegenden berlegungen.
Wir knnen auch die roten Quadrate halbieren und die blauen Quadrate vierteilen gem§ Abbildung 14. Dann haben wir ausschlie§lich rechtwinklig gleichschenklige Dreiecke.
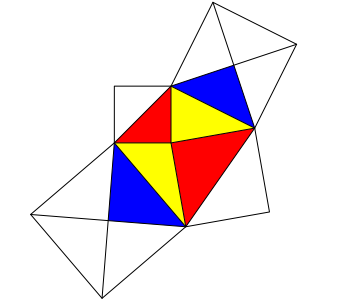
Abb. 14: Blau = rot
6 Schiefer Pythagoras
Die Abbildung 15 zeigt dasselbe wie die Abbildung 14, aber ohne Zustze.

Abb. 15: Blau = rot
Im Folgenden einige Eigenschaften der Figur der Abbildung 15.
6.1 Umkreise
Die Umkreise (Thaleskreise) der vier rechtwinklig gleichschenkligen Dreiecke verlaufen durch einen gemeinsamen Punkt (Abb. 16).

Abb. 16: Umkreise
Den Grund dafr werden wir gleich einsehen.
6.2 Diagonalen
Wir zeichnen zwei Diagonalen (ãDurchmesserdiagonalenÒ) gem§ Abbildung 17.
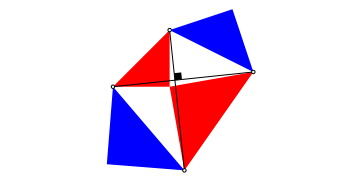
Abb. 17: Diagonalen
Die beiden Diagonalen sind gleich lang und orthogonal. Fr den Beweis verwenden wir die beiden in der Abbildung 18 grau eingezeichneten Dreiecke. Diese gehen durch eine Drehung um 90¡ um den gemeinsamen Punkt der beiden roten rechtwinklig gleichschenkligen Dreiecke auseinander hervor.
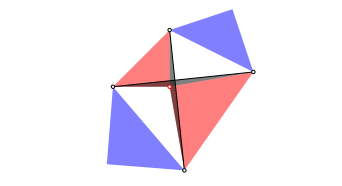
Abb. 18: Beweisdreiecke
Damit ist auch die Schnittpunkteigenschaft der vier Umkreise (Abb. 16) bewiesen.
6.3 Inversion
Wir klappen die beiden roten rechtwinklig gleichschenkligen Dreiecke nach au§en und dafr die beiden blauen nach innen (Abb. 19).

Abb. 19: Inversion
Die beiden blauen Dreieck haben die Spitze gemeinsam. Fr den Beweis zeichnen wir die beiden Thaleskreise ber den Basen der blauen Dreiecke (vgl. Abb. 16). Diese Thaleskreise verlaufen durch den Schnittpunkt der beiden orthogonalen Diagonalen gleicher Lnge. Sie haben aber noch einen zweiten Schnittpunkt. Die beiden in der Abbildung 20 braun eingezeichneten Dreiecke mit einem gemeinsamen Eckpunkt in diesem zweiten Schnittpunkt sind daher rechtwinklig.
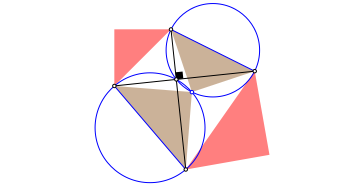
Abb. 20: Zweiter Schnittpunkt der Thaleskreise
Um zu zeigen, dass sie auch rechtwinklig sind, arbeiten wir mit den beiden in der Abbildung 21 eingezeichneten grauen Dreiecken.
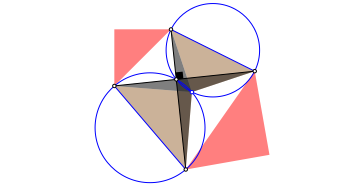
Abb. 21: Die beiden grauen Dreiecke
Entsprechende Seiten dieser beiden grauen Dreiecke stehen je orthogonal zueinander. Die beiden grauen Dreiecke sind also hnlich. Da sie aber zudem in einer Seite (den gleich langen orthogonalen Diagonalen) bereinstimmen, sind sie sogar kongruent. Daher sind die beiden braunen Dreiecke rechtwinklig gleichschenklig. Sie stimmen mit den eingeklappten blauen Dreiecken berein.
Die beiden in der Abbildung 22 eingezeichneten grnen Dreiecke sind zunchst untereinander flchengleich. Der Beweis geht analog zur Flchengleichheit der beiden gelben Dreiecke (Abb. 4).

Abb. 22: Flchengleiche grne Dreiecke
Wegen der Flchengleichheit von rot zu blau und der Invarianz des durch die beiden orthogonalen Diagonalen aufgespannten Viereckes sind die grnen Dreiecke auch flchengleich zu den gelben Dreiecken.
6.4 Noch mehr Diagonalen
In der Figur der Abbildung 23 sind zwei weitere Diagonalen eingezeichnet.
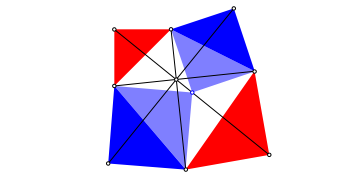
Abb. 23: Zwei weitere Diagonalen
Diese
langen Diagonalen verlaufen ebenfalls durch den Schnittpunkt der kurzen Diagonalen,
schneiden diese unter Winkeln von 45¡ und sind ![]() mal so
lang wie die kurzen Diagonalen. Wir zeigen dies exemplarisch fr diejenige
lange Diagonale, welche die beiden Au§enecken der blauen Dreiecke verbindet
(Abb. 24).
mal so
lang wie die kurzen Diagonalen. Wir zeigen dies exemplarisch fr diejenige
lange Diagonale, welche die beiden Au§enecken der blauen Dreiecke verbindet
(Abb. 24).
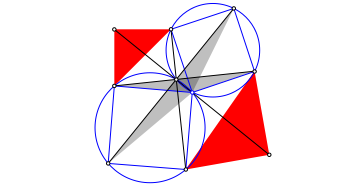
Abb. 24: Beweisfigur
Das
kleine graue Dreieck kann auf das gro§e graue Dreieck abgebildet werden mit
einer Drehstreckung um den zweiten Schnittpunkt der beiden Thaleskreise. Der
Drehwinkel ist 45¡, der Streckfaktor ![]() .
.
Die Abbildung 25 zeigt zum Vergleich ein quadratisches Arrangement mit denselben Winkel- und Lngenverhltnissen bei den Diagonalen.

Abb. 25: Quadratisches Arrangement
Bei der Abbildung 23 haben wir es mit einem schiefen Quadrat zu tun.
6.5
6.6 Parkett
Wir knnen die Figur der Abbildung 15 zu einem Parkett erweitern (Abb. 26). Die dabei entstehenden neuen Zwischendreiecke sind grn markiert. Die grnen Zwischendreiecke sind flchengleich zu den gelben.

Abb. 26: Parkett
In dieser Parkettierung fallen einerseits rot-gelbe Vierecke auf und andererseits blau-grne Vierecke an. Die beiden Vierecktypen haben punktsymmetrische Umrisse, aber unterschiedliche Binnenunterteilungen.