Hans Walser, [20170104a]
Schiefer Pythagoras
Anregung: Max Bill: Konstruktion auf der Formel a2 + b2 = c2 (1937)
1 Parallelogramme statt Quadrate
Die Abbildung 1 zeigt eine schiefe Pythagoras-Figur.

Abb. 1: Schiefer Pythagoras
Die Abbildung 2 zeigt den Link zur schulm§igen Pythagoras-Figur.
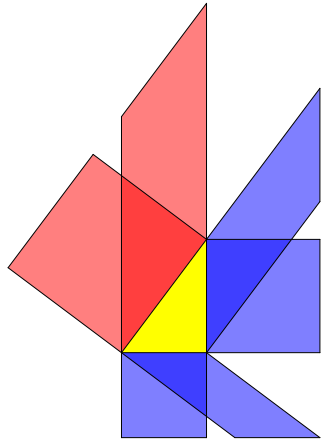
Abb. 2: Link zur bekannten Figur
Die Figur der Abbildung 1 kann zu einem Parkett ergnzt werden (Abb. 3). Die grnen rechtwinkligen Dreiecke sind hnlich zu den gelben. Die Parallelogramme passen auch bei den grnen rechtwinkligen Dreiecken zum Satz des Pythagoras.

Abb. 3: Parkett
2 Rhomben statt Quadrate
2.1 Beispiel
Die Abbildung 4 zeigt eine Situation mit Rhomben.

Abb. 4: Rhomben statt Quadrate
Es gibt auch hierzu ein Parkett (Abb. 5).
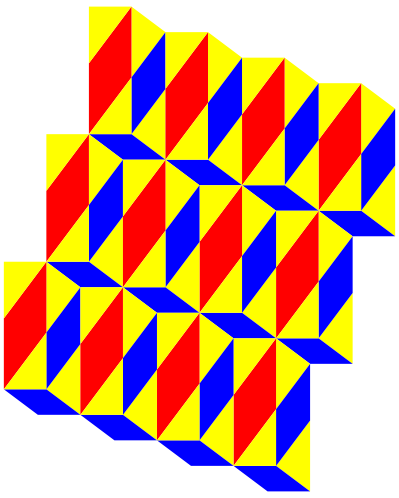
Abb. 5: Parkett
Man hat einige Mhe, in diesem Parkett die Pythagoras-Figur zu erkennen. Dies vor allem dann, wenn das Parkett seitenparallel gezeichnet ist (Abb. 6).

Abb. 6: Andere Lage des Parketts
2.2 Zweite Lsung
Die Abbildung 7 zeigt, dass es zum gleichen rechtwinkligen Dreieck eine zweite Lsung gibt.

Abb. 7: Zwei Lsungen
In der einen Lsung erscheint der eine der beiden spitzen Winkel des rechtwinkligen Dreiecks als spitzer Rhomben-Winkel, in der anderen Lsung entsprechend der zweite der beiden spitzen Winkel.
Umgekehrt kann zu jedem Rhombus, mit Ausnahme des Quadrates, ein rechtwinkliges Dreieck gefunden werden, so dass der Rhombus (in drei verschiedenen Gr§en) zusammen mit dem Dreieck in ein Parkett obiger Art passt.
2.3 Sonderflle
In der Abbildung 8 wurde ein rechtwinklig gleichschenkliges Dreieck als Ausgangsfigur gewhlt. Aus Symmetriegrnden gibt es in diesem Sonderfall nur eine Lsung.
Die blauen Rhomben sind in diesem Sonderfall alle gleich gro§.
Wir unterliegen aber einer optischen Tuschung, indem wir die waagerechten blauen Rhomben gr§er sehen als die senkrechten. Die optische Tuschung kommt daher, dass die senkrechten Rhomben neben den um einiges gr§eren roten Rhomben stehen und daher klein erscheinen.

Abb. 8: Rechtwinklig gleichschenkliges Dreieck
Die Abbildung 9 zeigt die beiden Lsungen fr das 30¡-60¡-90¡-Dreieck.
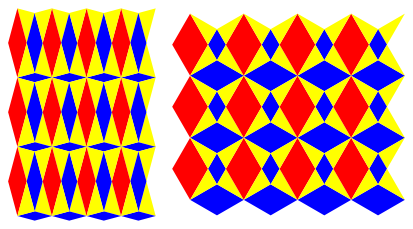
Abb. 9: 30¡-60¡-90¡-Dreieck
In der zweiten Lsung knnen die gro§en Rhomben zerlegt werden (Abb. 10).

Abb. 10: Nur zwei Sorten Rhomben
Die Rhomben knnen auch in gleichseitige Dreiecke aufgelst werden (Abb. 11).

Abb. 11: Gleichseitige Dreiecke statt Rhomben