Hans Walser, [20210125]

SchlaufenberŸhrung

1     Worum geht es?

Sich berŸhrende Schlaufen bei verlŠngerten Zykloiden

2     Die Kurven

Wir arbeiten mit Kurven mit der Parameterdarstellung:

 

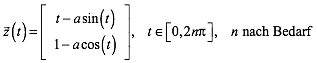                                (1)

 

 

 

 

 

3     Zykloiden

FŸr a = 0 erhalten wir eine horizontale Gerade.

FŸr a = 1 ergibt sich die Zykloide (Abb. 1).

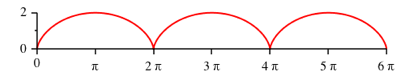
Abb. 1: Zykloide

FŸr a > 1 erhalten wir eine sogenannte verlŠngerte Zykloide, welche Schlaufen enthŠlt. Die Abbildung 2 zeigt die Kurve fŸr a = 3.

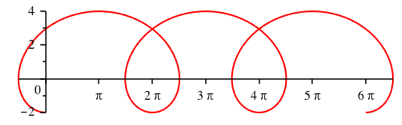
Abb. 2: VerlŠngerte Zykloide

4     Problemstellung

FŸr welchen Wert von a berŸhren sich benachbarte Schlaufen (Abb. 3)?

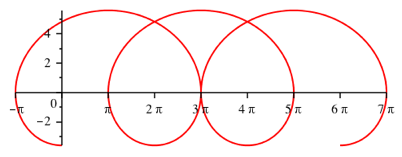
Abb. 3: BerŸhrende Schlaufen

5     Bearbeitung

Aus SymmetriegrŸnden sind in den BerŸhrungspunkten die Kurventangenten senkrecht. Aus (1) gewinnen wir den Tangentialvektor:

 

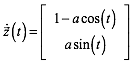                                                                                             (2)

 

 

 

 

 

Senkrechtstehen hei§t, dass die erste Komponente des Tangentialvektors null sein muss, also:

 

                                                                                                           (3)

 

 

 

Ein Vergleich mit (1) zeigt, dass die BerŸhrungspunkte auf der x-Achse liegen.

Wiederum aus SymmetriegrŸnden mŸssen die BerŸhrungspunkte bei ungeraden Vielfachen von ¹ liegen. Somit erhalten wir (zusammen mit (3)) fŸr den ersten Durchgang der Kurve durch die x-Achse die Bedingungen:

 

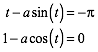                                                                                                         (4)

 

 

 

 

 

Dies ist ein transzendentes Gleichungssystem fŸr a und t. Mit numerischen Methoden (fsolve) erhalten wir a = 4.603338849 und t = 1.351816804.

6     Verallgemeinerung

FŸr mittelbar benachbarte Schlaufen (Abb. 4) haben wir das Gleichungssystem:

 

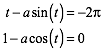                                                                                                       (5)

 

 

 

 

 

Es hat die Lšsungen a = 7.789705768 und t = 1.442066530.

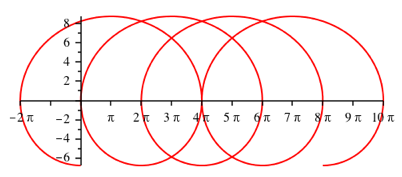
Abb. 4: Mittelbar benachbarte Schlaufen berŸhren sich

Wir sehen wie der Hase lŠuft. Im allgemeinen Fall gilt das Gleichungssystem:

 

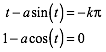                                                                                                       (6)

 

 

 

 

 

Die Tabelle 1 gibt die ersten Lšsungen.

Dabei sind auch noch die BogenlŠngen, bezogen auf ein Parameterintervall fŸr t der LŠnge 2¹ eingetragen. Bei der Zykloide gibt es eine ãschšneÒ Zahl, nachher nicht mehr.

 

k

a

t

BogenlŠnge

0

1

0

8

1

4.603338849

1.351816804

29.26587933

2

7.789705768

1.442066530

49.14602367

3

10.94987987

1.479343699

68.94365255

4

14.10169534

1.499823299

88.71499063

5

17.24976557

1.512792004

108.4745546

Tab. 1: Einige Lšsungen

Nachfolgend die zugehšrigen Kurven.

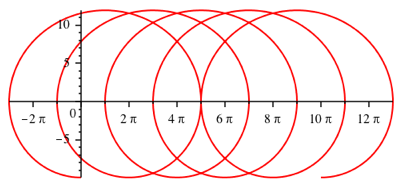
Abb. 5.1: k = 3

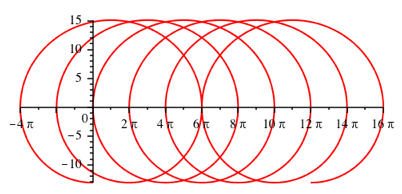
Abb. 5.2: k = 4

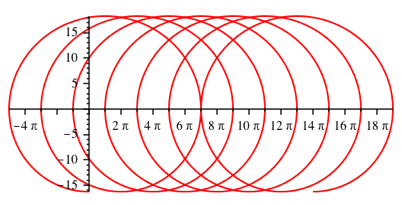
Abb. 5.3: k = 5