Hans Walser, [20150120]

Schleppkurven

Anregung: H.-G. W., W.

1     Problemstellung

Ein Punkt Z bewegt sich auf einer Zugkurve  und zieht an einer Leine einen Punkt W. Dieser bewegt sich auf der gesuchten Schleppkurve .

2     Differentielle Beschreibung

Es sei  der Leinenvektor. Dann gilt:

 

 

Mit Angabe des Startpunktes der Schleppkurve ist diese bestimmt.

3     Beispiele

Die Beispiele sind iterativ nach Euler approximativ berechnet worden. Die Zugkurve ist rot, die Schleppkurve blau gezeichnet. Die Startpunkt sind markiert.

3.1    Traktrix

Der Klassiker. Die Zugkurve ist eine Gerade. Die Traktrix geht asymptotisch gegen die Zugkurve.

 

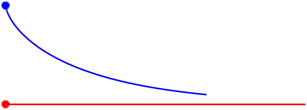
Abb. 1: Traktrix

 

3.2    Im Kreis

 

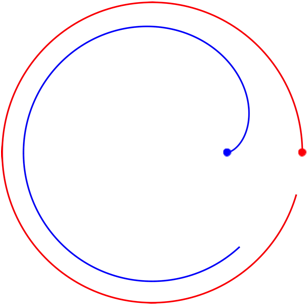
Abb. 2: Im Kreis

 

3.3    Startpunkt au§erhalb des Kreises

 

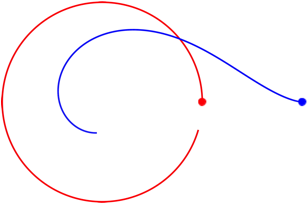
Abb. 3: Startpunkt au§erhalb des Kreises

 

3.4    Im Quadrat

 

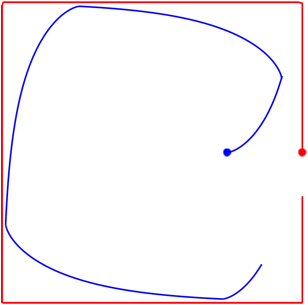
Abb. 4: Im Quadrat

 

3.5    Startpunkt au§erhalb

 

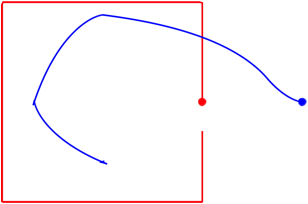
Abb. 5: Startpunkt au§erhalb

 

3.6    Wellenlinie

 

Abb. 6: Wellenlinie

 

Die Schleppkurve hat eine kleinere Amplitude und hinkt hinterher. Damit kann aus dem Kurvenbild auch ohne die Farben entschieden werden, welches die Zugkurve und welches die Schleppkurve ist.

4     Programm

Nachfolgend das Maple-Programm fźr die Situation der Abbildung 3.

restart: with(plots): with(plottools):

 

T:=6:              # Obergrenze Parameter

 

deltat:=0.01:      # SchrittlŠ*nge

 

z1:=t->cos(t):     # Erste Koordinate der Zugkurve

z2:=t->sin(t):     # Zweite Koordinate der Zugkurve

 

w1[0]:=2:          # Erste Koordinate Startposition Schleppkurve

w2[0]:=0:          # Zweite Koordinate Startposition Schleppkurve

 

Zugstart:=point([z1(0),z2(0)], color=red, symbolsize=20, symbol=solidcircle):

Zugkurve:=plot([z1(t),z2(t),t=0..T], color=red, thickness=2):

 

N:=floor(T/deltat):

for n from 0 to N do

 p1[n]:=evalf(z1(n*deltat))-w1[n]: p2[n]:=evalf(z2(n*deltat)-w2[n]):

 dz1[n]:=z1((n+1)*deltat)-z1(n*deltat):

 dz2[n]:=z2((n+1)*deltat)-z2(n*deltat):

 Faktor[n]:=evalf((p1[n]*dz1[n]+p2[n]*dz2[n])/(p1[n]^2+p2[n]^2)):

 dw1[n]:=p1[n]*Faktor[n]: dw2[n]:=p2[n]*Faktor[n]:

 w1[n+1]:=w1[n]+dw1[n]: w2[n+1]:=w2[n]+dw2[n]:

end:

 

Schleppstart:=point([w1[0],w2[0]], color=blue, symbolsize=20, symbol=solidcircle):

Schleppkurve:=seq(line([w1[n],w2[n]],[w1[n+1],w2[n+1]], color=blue, thickness=2), n=0..N):

 

display([Zugstart, Zugkurve, Schleppstart, Schleppkurve], scaling=constrained, axes=none);

 

Literatur

Schierscher, Georg (1995): Verfolgungsprobleme. Berichte źber Mathematik und Unterricht. ETH Zźrich.

Schierscher, Georg (1997): Verfolgungsprobleme. MU, Der Mathematikunterricht. 43/3.