Hans Walser, [20061210d]

Eine Schließungsfigur mit Schnittpunkt

1 Die Figur

Auf die folgende Figur bin ich gestoßen, indem ich bei drei paarweise sich berührenden Kreisen von einem Kreispunkt über den Berührungspunkt zu einem Nachbarkreis gegangen bin.

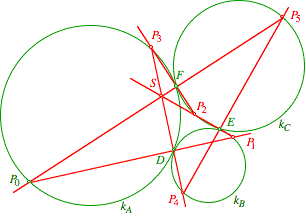
Die Figur

2 Disposition

Wir beginnen mit drei Kreisen , welche sich paarweise in berühren. Ferner wählen wir einen beliebigen Punkt .

Ausgangslage

Nun konstruieren wir Punkte wie folgt.

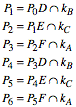
3 Vermutungen

Aus der Figur lesen wir folgende Vermutungen ab:

a) , wir haben eine so genannte Schließungsfigur.

b) (Orthogonalität)

c) sind kopunktal, den gemeinsamen Schnittpunkt nennen wir S. Ebenso sind kopunktal (in der Figur nicht eingezeichnet).

4 Beweise

Die Zentren der drei Kreise bilden ein Dreieck, dessen Seiten durch verlaufen. Aus Peripheriewinkelsätzen ergeben sich die eingezeichneten Winkel.

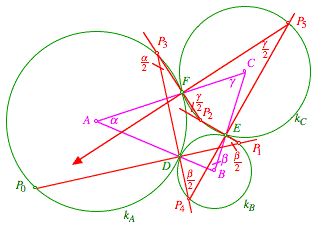
Winkel

4.1 Beweis der Schließungseigenschaft

Es sei . Wir haben zu zeigen, dass .

Zunächst ergeben sich folgende Winkel:

Den Winkel können wir über die Winkelsumme des Sechseckes berechnen. Nun aber Vorsicht: dieses Sechseck ist selbstüberkreuzend. Es hat die Umlaufszahl 2, daher ist die Summe der Außenwinkel = . Zusammen mit der Innenwinkelsumme muss das ergeben, nämlich π pro Eckpunkt. Somit ist in unserem Fall: . In unserem Fall heißt das:

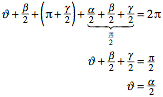
Der Punkt Q liegt somit auf dem Ortsbogen . Damit ist die Schließungseigenschaft bewiesen. Wir dürfen also mit folgender Figur weiterarbeiten:

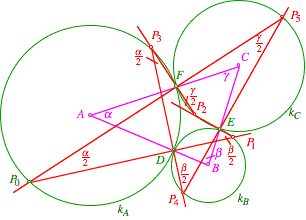
Schließungsfigur und Winkel

4.2 Beweis der Orthogonalität

Wir zeigen exemplarisch . Im Viereck haben wir die Innenwinkelsumme:

4.3 Beweis der Schnittpunktseigenschaft

Für den Beweis der Schnittpunktseigenschaft benötigen wir den Inkreis des Dreieckes ABC. Dieser berührt die Dreiecksseiten in den Punkten (Überlegung: gleich lange Tangentenabschnitte). Sein Mittelpunkt sei I.

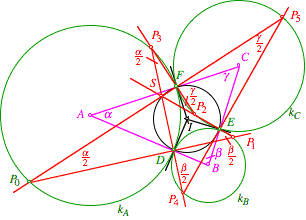
Figur mit Inkreis

Wir zeigen, dass der vermutete Schnittpunkt S existiert und auf dem Inkreis liegt.

Es sei zunächst . Das rechtwinklige Dreieck hat bei den Winkel . Nun ist aber , der obere Inkreisbogen ED ist also Ortsbogen für den Winkel . Daher liegt auf dem Inkreis.

Weiter sei . Das rechtwinklige Dreieck hat bei den Winkel . Nun ist aber , der linke Inkreisbogen FE ist also Ortsbogen für den Winkel . Daher liegt ebenfalls auf dem Inkreis.

Damit ist die Schnittpunktseigenschaft beweisen.

Bemerkung: Den zweiten Schnittpunkt, als den gemeinsamen Punkt von , erhalten wir, indem wir S am Inkreismittelpunkt I spiegeln. Der Beweis sei der Leserin überlassen. Der Thaleskreis lässt schön grüßen.