Hans Walser, [20150202]

Schließungsfigur mit Kreisen

1 Die Schließungsfigur

Wir wählen ein (unregelmäßiges) n-Eck und einen beliebigen Punkt M. Die Abbildung 1 zeigt die Situation für n = 5. Auf der Geraden wählen wir einen Startpunkt .

Abb. 1: Disposition

Den zweiten Schnittpunkt des Kreises durch M, und mit der Geraden bezeichnen wir mit (Abb. 2).

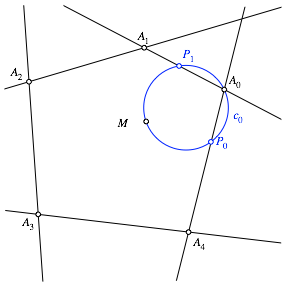
Abb. 2: Folgepunkt

Und nun iterieren wir: ist der zweite Schnittpunkt des Kreises durch M, und mit der Geraden .

Dann ist , wir haben eine Schließungsfigur (Abb. 3).

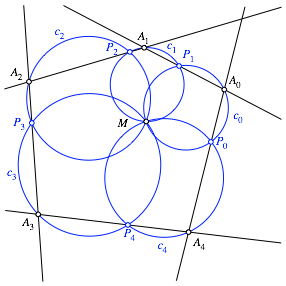
Abb. 3: Schließungsfigur

2 Beweis

Das Viereck ist ein Sehnenviereck. Daher ergänzen sich die Winkel und auf 180°. Damit ist aber der Nebenwinkel gleich groß wie . Allgemein sind alle Winkel untereinander gleich groß. Das beweist die Schließungseigenschaft. Die Schließungseigenschaft ist unabhängig von n.

Die Abbildung 4 zeigt die relevanten Sehnenvierecke.

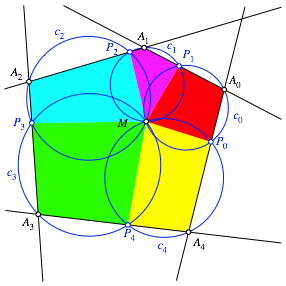
Abb. 4: Sehnenvierecke

3 Shortcut

Die Diagonale verläuft durch den zweiten Schnittpunkt der beiden Kreise und (Abb. 5).

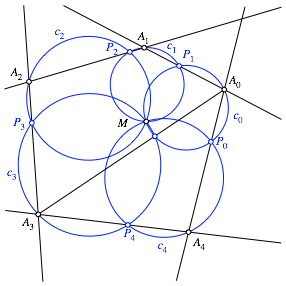
Abb. 5: Shortcut

Das ist klar, denn wir hätten statt mit dem Fünfeck auch mit dem Viereck operieren können.

Allgemein verläuft die Gerade durch den Schnittpunkt der beiden Kreise und (Abb. 6).

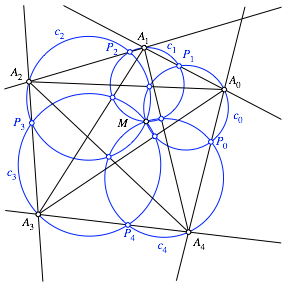
Abb. 6: Seiten und Diagonalen

Die Abbildung 7 zeigt dieselbe Situation für n = 7.

Abb. 7: Siebeneck

4 Kreise gegeben

Natürlich kann auch umgekehrt vorgegangen werden: Wir gegen n Punkte vor sowie einen Punkt M. Dann zeichnen wir Kreise durch M, und (Abb. 8). Auf dem Kreis wählen wir einen Startpunkt .

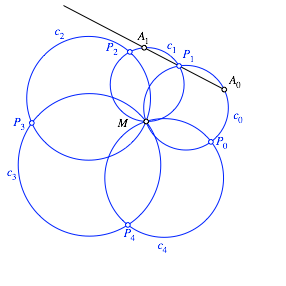
Abb. 8: Umgekehrtes Vorgehen

Den Punkt finden wir nun als Schnittpunkt der Geraden mit dem Kreis .

Entsprechend finden wir die übrigen Punkte und erhalten eine Schließungsfigur (Abb. 9).

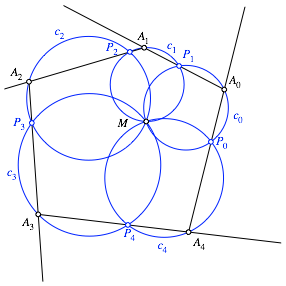
Abb. 9: Schließungsfigur