1 Worum geht es?

Eine Schließungsfigur der Periodenlänge 3 im Kreis

Link mit Höhenschnittpunkt

2 Konstruktion

Wir zeichnen einen Kreis und wählen einen beliebigen Punkt auf der Kreislinie und einen beliebigen Punkt im Innern des Kreises (Abb. 1).

Abb. 1: Kreis mit Kreispunkt und einem Punkt im Innern

Wir passen ein Drachenviereck ein (Abb. 2). Der Punkt auf der Kreislinie soll auf der Symmetrieachse liegen, der Punkt im Innern nicht. Die Konstruktion geht so: Wir zeichnen einen Kreis um den Punkt auf der Kreislinie durch den Punkt im Innern und schneiden mit dem Startkreis. Die Mittelsenkrechte des Schnittpunktes und des Punktes im Innern ist die Symmetrieachse des Drachenviereckes. Nun schneiden wir noch die Symmetrieachse mit dem Startkreis.

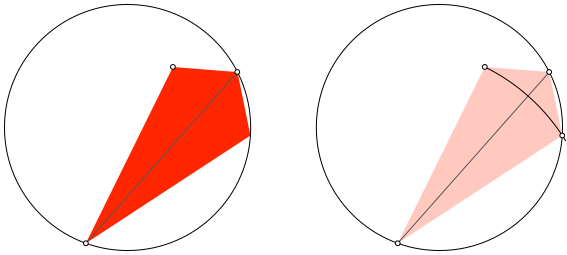
Abb. 2: Drachenviereck

Nun passen wir analog ein zweites Drachenviereck ein (hellblau in Abb. 3).

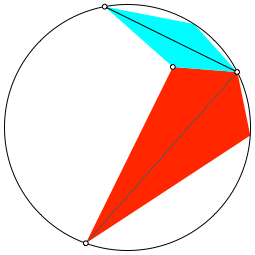
Abb. 3: Zweites Drachenviereck

Wenn wir nun ein weiteres Drachenviereck einpassen, schließt sich die Figur (Abb. 4).

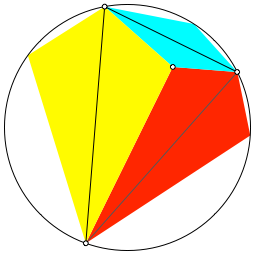
Abb. 4: Schließungsfigur

Die Schließungseigenschaft ist unabhängig vom gewählten Kreispunkt (Abb. 5).

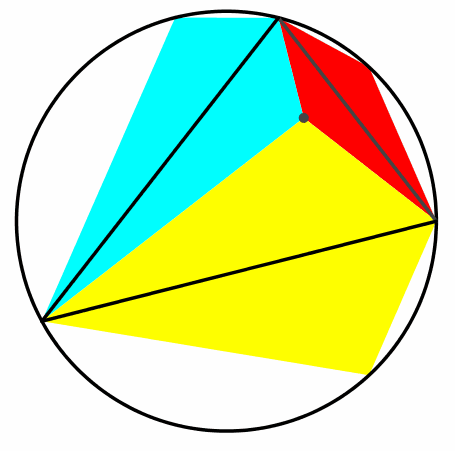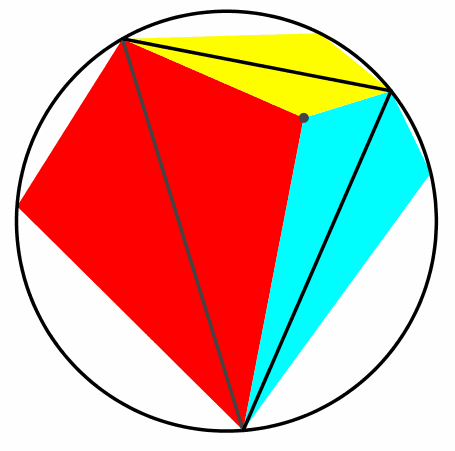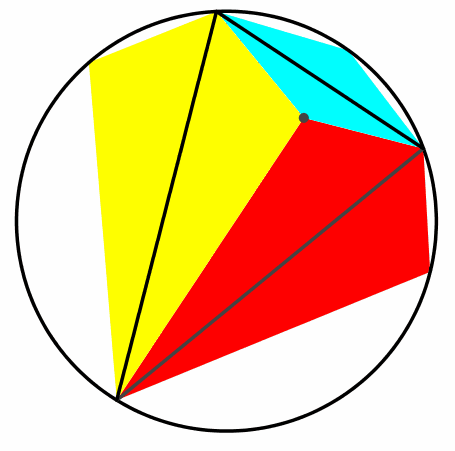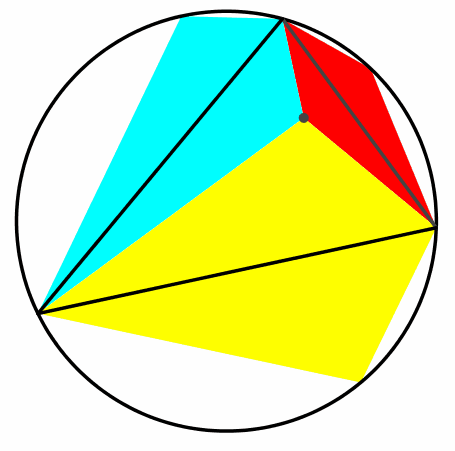
Abb. 5: Schließungsfiguren

3 Hintergrund

Wenn wir zu einem beliebigen Dreieck die Höhen, den Höhenschnittpunkt und den Umkreis zeichnen, können wir zusätzlich drei Drachenvierecke einzeichnen (Abb. 6). Dies kann mit Winkelüberlegungen eingesehen werden.

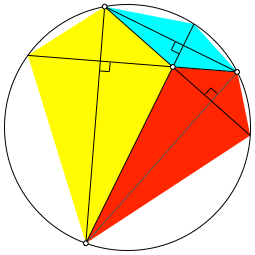
Abb. 6: Höhen im Dreieck

Wir haben nun umgekehrt zu gegebenem Umkreis, gegebenem Höhenschnittpunkt und einer Dreiecksecke das Dreieck rekonstruiert.

Passende Schulaufgabe: Von einem Dreieck ABC kennt man die Ecke A, den Umkreismittelpunkt U und den Höhenschnittpunkt H. Gesucht ist das Dreieck.