Hans Walser, [20230504]
Schließungsfigur
Idee und Anregung: Maik Rentsch
1 Worum geht es?
Eine Schließungsfigur im Kontext von Pentagon und Pentagramm.
2 Die Figur
Auf einer Seite eines regelmäßigen Fünfeckes wählen wir einen grünen Startpunkt (Abb. 1), eher rechts von der Mitte.
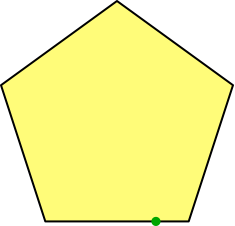
Abb. 1: Startpunkt
Wir zeichnen nun eine Senkrechte zur Fünfeckseite durch diesen Startpunkt und schneiden diese mit der übernächsten Fünfeckseite (im positiven Drehsinn gezählt) (Abb. 2).
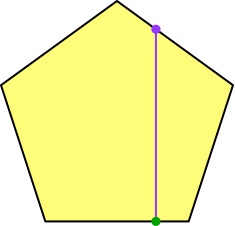
Abb. 2: Erster Schnitt
Von diesem Punkt aus zeichnen wir wiederum eine Senkrechte zur Fünfeckseite und schneiden mit der übernächsten Fünfeckseite (Abb. 3).
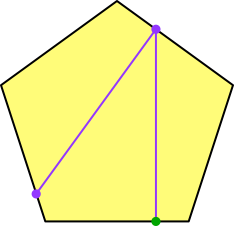
Abb. 3: Zweiter Schritt
Entsprechend geht es weiter (Abb. 4, 5, 6).
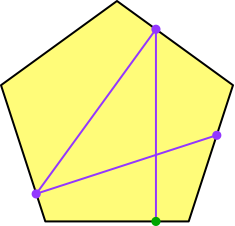
Abb. 4: Dritter Schritt
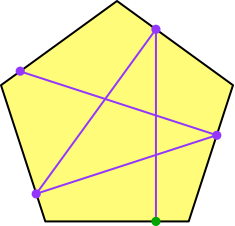
Abb. 5: Vierter Schritt
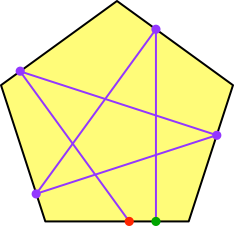
Abb. 6: Fünfter Schritt
In unserem Beispiel kommen wir nach dem fünften Schritt zwar auf die Ausgangsseite des Fünfeckes zurück, aber nicht auf den Startpunkt.
3 Verschieben des Startpunktes
In der Abbildung 7 wird der Startpunkt verschoben.
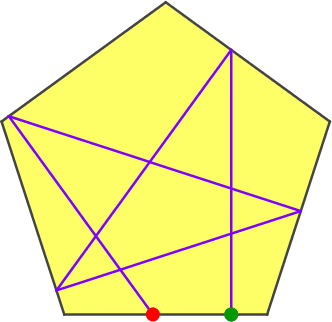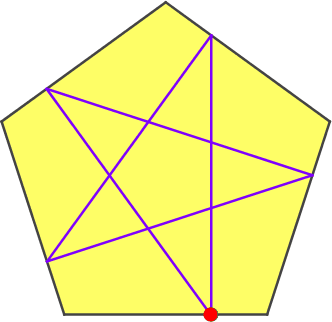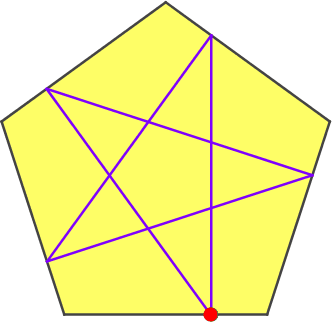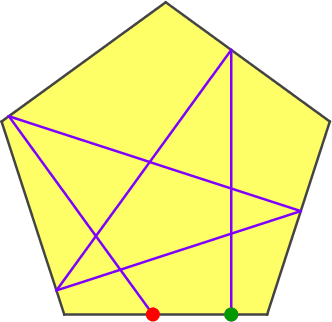
Abb. 7: Verschieben des Startpunktes
Wir sehen, dass es eine Position des Startpunktes gibt, welche zu einer Schließungsfigur (Pentagramm) führt. Wo ist diese Startposition?
4 Stern
Wir spiegeln das Fünfeck an seinem Mittelpunkt (Abb. 8).
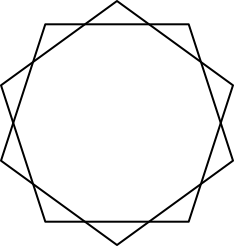
Abb. 8: Spiegeln am Mittelpunkt
Dadurch entsteht ein Stern mit zehn Spitzen (Abb. 9).

Abb. 9: Stern
Die Spitzen sind gleichschenklige Dreiecke mit Basiswinkeln 36° (Abb. 10). Ihre Seitenlängen stehen im Verhältnis des Goldenen Schnittes. Die Schenkel sind Minore, die Basis ein Major.
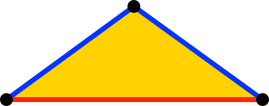
Abb. 10: Spitze im Goldenen Schnitt
Diese Seitenverhältnisse können wir auf den Stern übertragen (Abb. 11).

Abb. 11: Seitenverhältnisse
5 Schließungsfigur
Nun können wir die Schließungsfigur einzeichnen (Abb. 12).
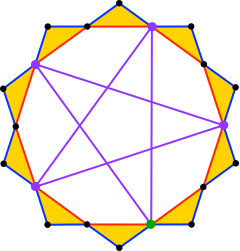
Abb. 12: Schließungsfigur
Der Startpunkt muss so gewählt werden, dass die Fünfeckseite im Verhältnis Minor-Major-Minor unterteilt wird (Abb. 13).
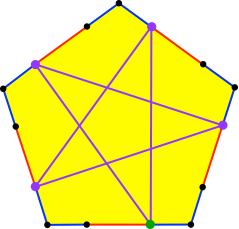
Abb. 13: Position des Startpunktes
Die nicht gebrauchten Teilpunkte führen zu einer spiegelbildlichen Lösung (Abb. 14).
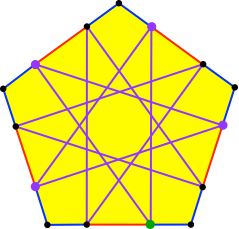
Abb. 14: Spiegelbildliche Lösung