Hans Walser, [20231102]
Schließungsfigur
Idee und Anregung: Helmut Mallas, Flensburg
1 Worum es geht
Schließungsfigur mit vorgegebener Periodenlänge
2 Beispiele
2.1 Periodenlänge 2
Wir zeichnen den Grafen der Funktion:
![]()
Der Graf ist eine Hyperbel (rot in Abb. 1). Weiter zeichnen wir die Gerade y = x (blau in Abb. 1).
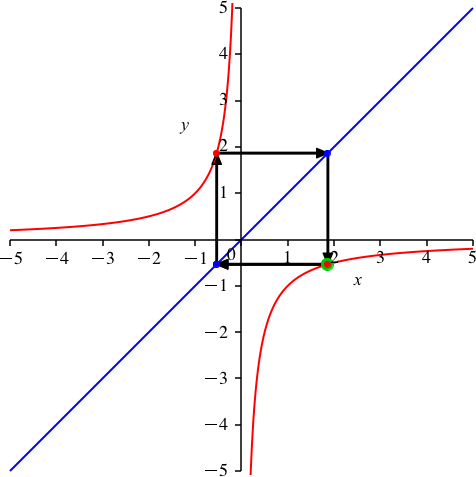
Abb. 1: Periodenlänge 2
Nun wählen wir auf der Hyperbel einen beliebigen Startpunkt (rot-grün in Abb. 1). Von diesem Startpunkt aus fahren wir horizontal bis zur blauen Gerade. Von dort vertikal bis zur Hyperbel (es ist nun der andere Hyperbelast). Dann wieder horizontal bis zur blauen Gerade und schließlich vertikal zur Hyperbel. Wir kommen zum Startpunkt zurück. Wir haben zwei Punkte auf der Hyperbel und zwei Punkte auf der Geraden. Daher die Periodenlänge 2.
Der Beweis für die Schließungseigenschaft ergibt sich aus der Symmetrie der Figur.
Die Figur ist eine Visualisierung des Sachverhaltes, dass die Verkettung der Funktion f mit sich selber die Identität ist.
2.2 Periodenlänge 3
Wir zeichnen nun den Grafen der Funktion:
![]()
Der Funktionsgraf ist ebenfalls eine Hyperbel (rot in Abb. 2). Die horizontale Asymptote ist auf dem Niveau 1.
Wir wählen wieder einen beliebigen Startpunkt auf der Hyperbel und verfahren wie im Beispiel der Abbildung 1.
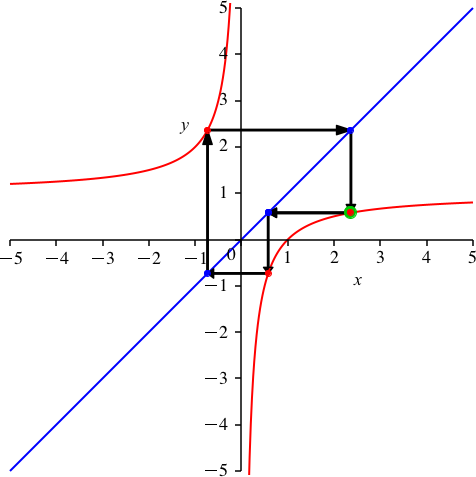
Abb. 2: Periodenlänge 3
Die Figur schließt sich erst nach drei Schritten. Die Schließungseigenschaft kann nicht mehr mit Symmetrieüberlegungen bewiesen werden. Die Abbildung 3 illustriert, wie der Startpunkt beliebig auf der Hyperbel gewählt werden kann.
Die Figur ist eine Visualisierung des Sachverhaltes, dass die dreimalige Verkettung der Funktion f die Identität ist.
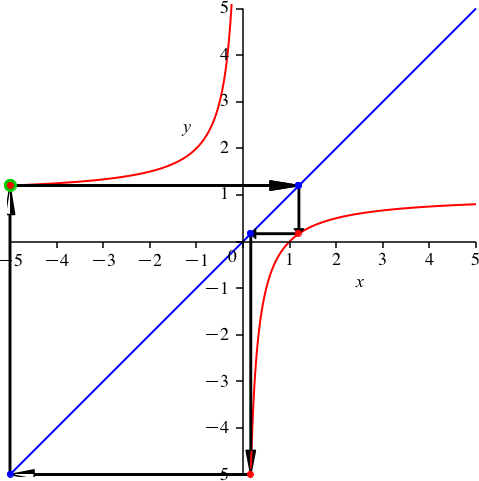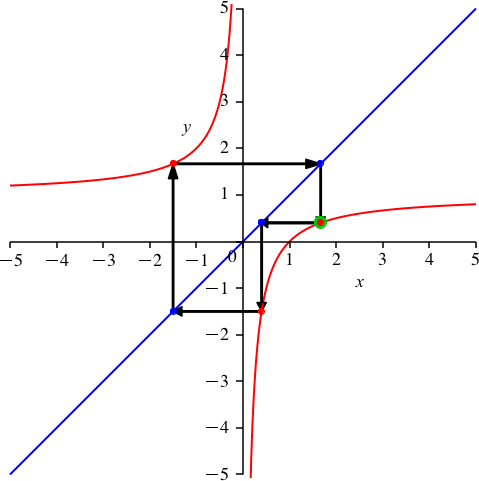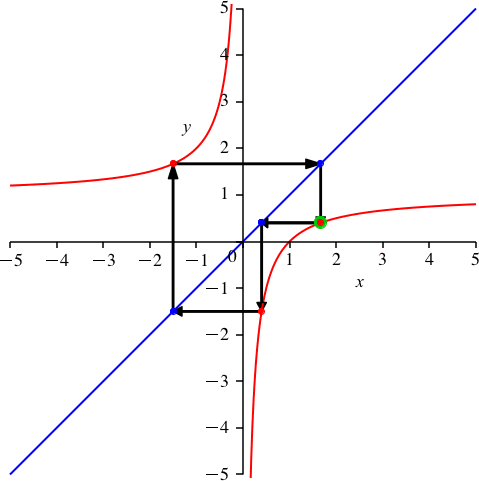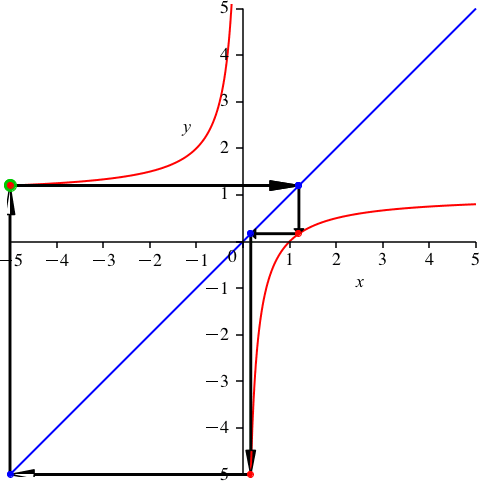
Abb. 3: Variation des Startpunktes
2.3 Periodenlänge 4
Mit dem Grafen der Funktion
![]()
ergibt sich eine Schließungsfigur der Periodenlänge 4 (Abb. 4).
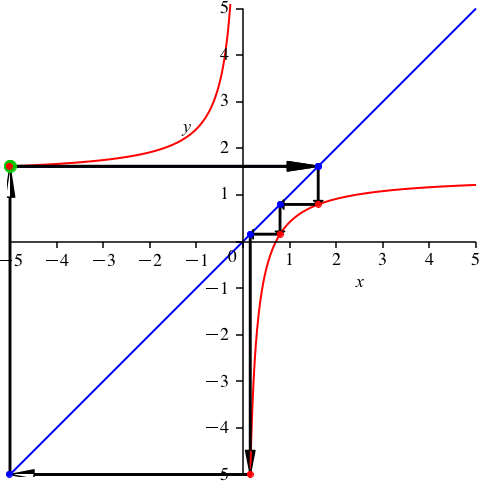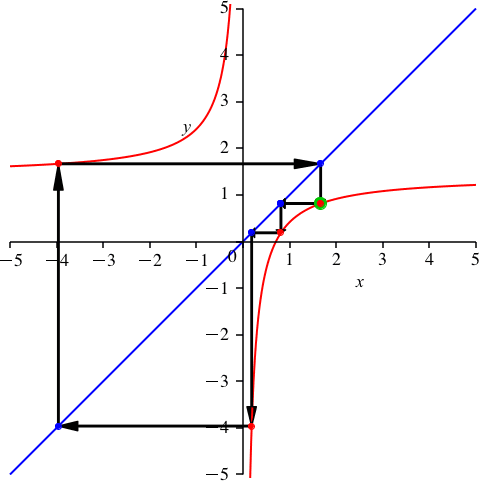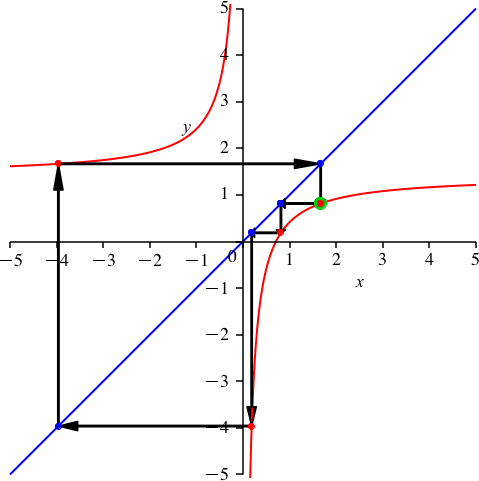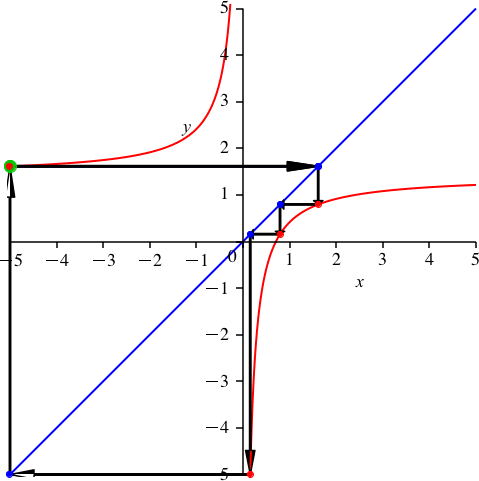
Abb. 4: Periodenlänge 4
2.4 Periodenlänge 5
Wir arbeiten mit dem Goldenen Schnitt:
![]()
Mit dem Grafen der Funktion
![]()
ergibt sich – wer hätte das gedacht – eine Schließungsfigur der Periodenlänge 5 (Abb. 5).
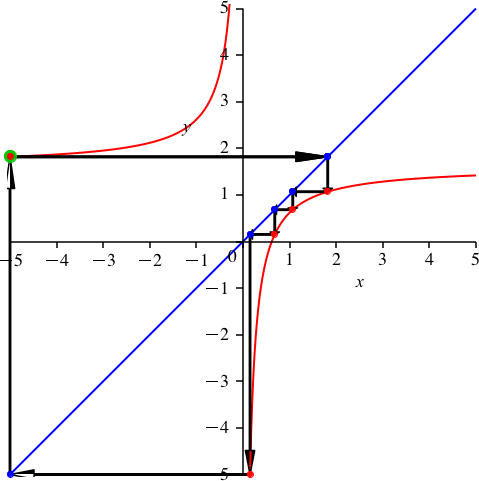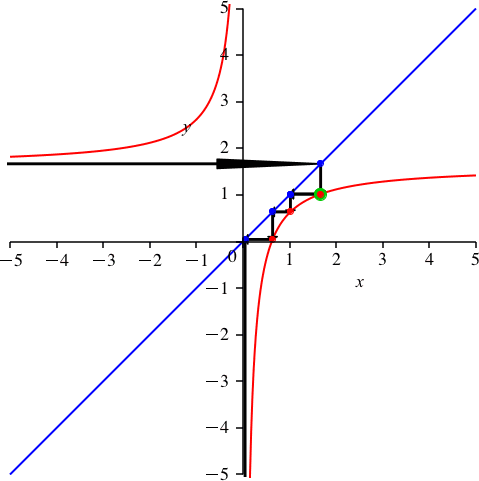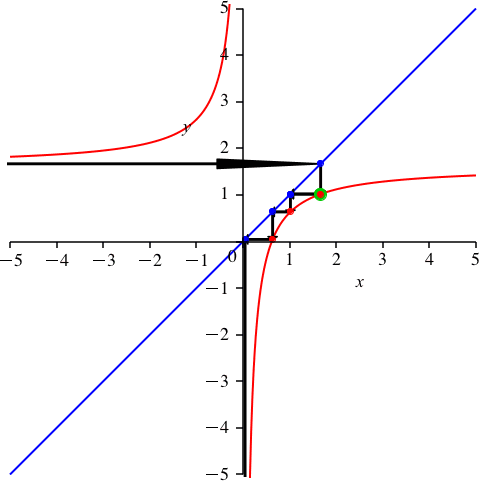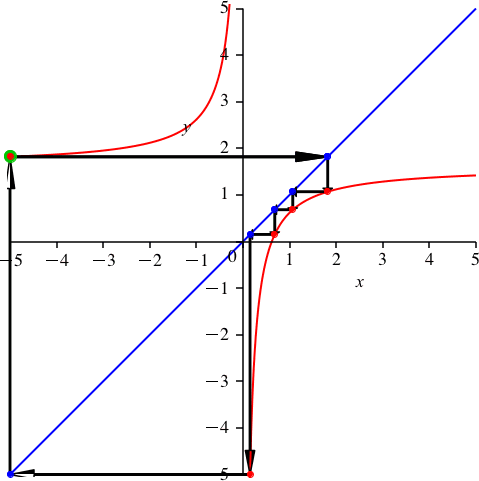
Abb. 5: Goldener Schnitt und Periodenlänge 5
3 Allgemein
Mit dem Grafen der Funktion
![]()
ergibt sich eine Schließungsfigur der Periodenlänge n.
Die Abbildungen 6 und 7 illustrieren das Beispiel für n = 9.
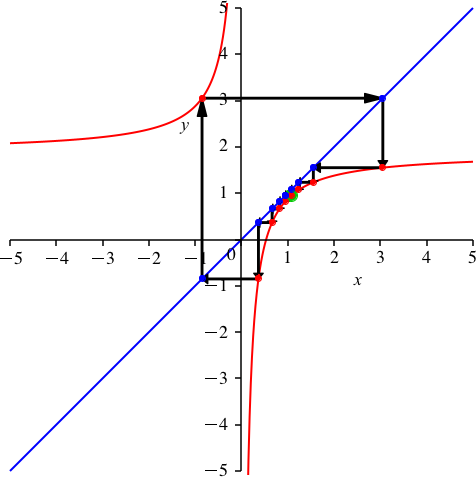
Abb. 6: Periodenlänge 9
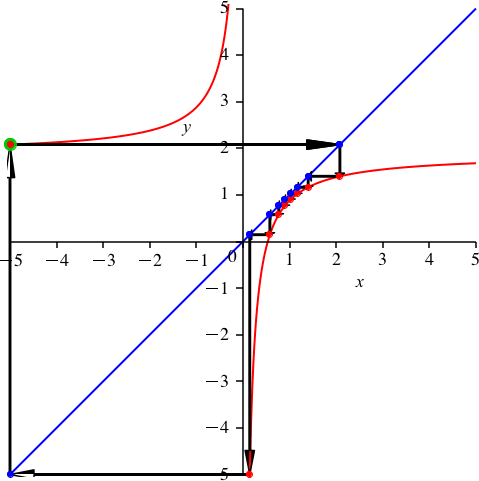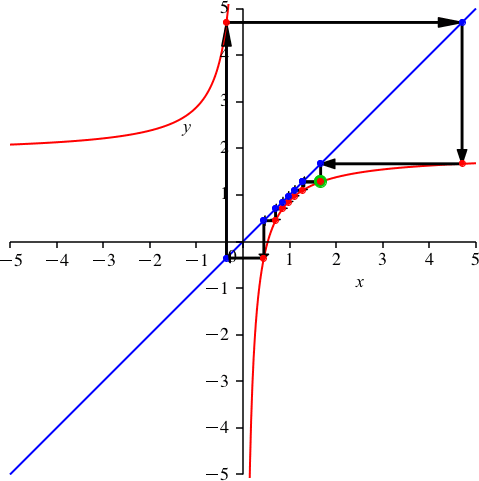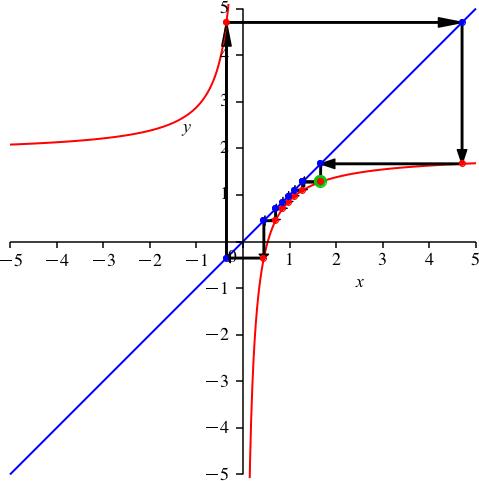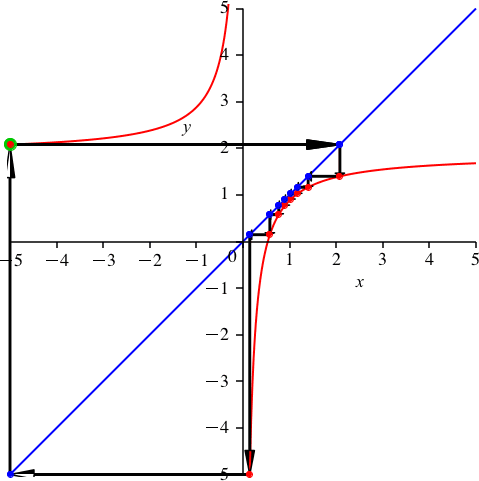
Abb. 7: Periodenlänge 9
4 Beweis
Der Beweis ist etwas abenteuerlich, der Autor hofft, dass er stimmt.
Wir haben zu zeigen, dass die n-malige Verkettung der Funktion
![]()
die Identität ist, also:
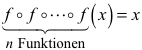
4.1 Rekursion
Mit beliebigem Startwert x0 definieren wir rekursiv die Folge:
![]()
Wir haben nun zu zeigen, dass diese Folge periodisch mit der Periodenlänge n ist. Dies machen wir aber über eine explizite Formel. Dazu brauchen wir die Fixpunkte der Funktion f.
4.2 Fixpunkte
Die Funktion
![]()
hat keine reellen Fixpunkte, das heißt keine reelle Zahlen ξ mit f(ξ) = ξ. Hingegen führt die Fixpunktbedingung f(ξ) = ξ, also
![]()
auf die quadratische Gleichung
![]()
mit den beiden konjugiert komplexen Lösungen:
![]()
Es ist:
![]()
4.3 Explizite Formel
Die mit dem Startwert x0 rekursiv definiere Folge
![]()
lässt sich nun explizit darstellen:
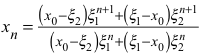
Dies ergibt sich aus der Formel von Binet (Walser 2012, S. 16) für verallgemeinerte Fibonacci-Folgen (in unserem Beispiel die verallgemeinerte Fibonacci-Folge mit den Startwerten 1 und x0).
Wegen
sind Zähler und Nenner in der expliziten Formel je antiperiodisch mit der Antiperiodenlänge n. Der Quotient ist daher periodisch mit der Periodenlänge n. Dies war zu zeigen.
Weblinks
Hans Walser: Schließungsfiguren
https://walser-h-m.ch/hans/Schliessungsfiguren/
Literatur
Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-60-8.