Hans Walser, [20230724]

Schließungsfigur mit Ellipsen

1 Die Schließungsfigur im Dreieck

Die Abbildung 1 zeigt eine Schließungsfigur der Periodenlänge 6 im Dreieck. Die Ellipsen haben jeweils eine Dreiecksecke und den Inkreismittelpunkt als Brennpunkte.

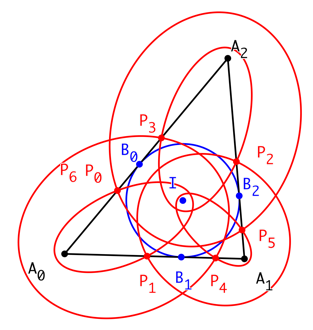
Abb. 1: Schließungsfigur mit Ellipsen

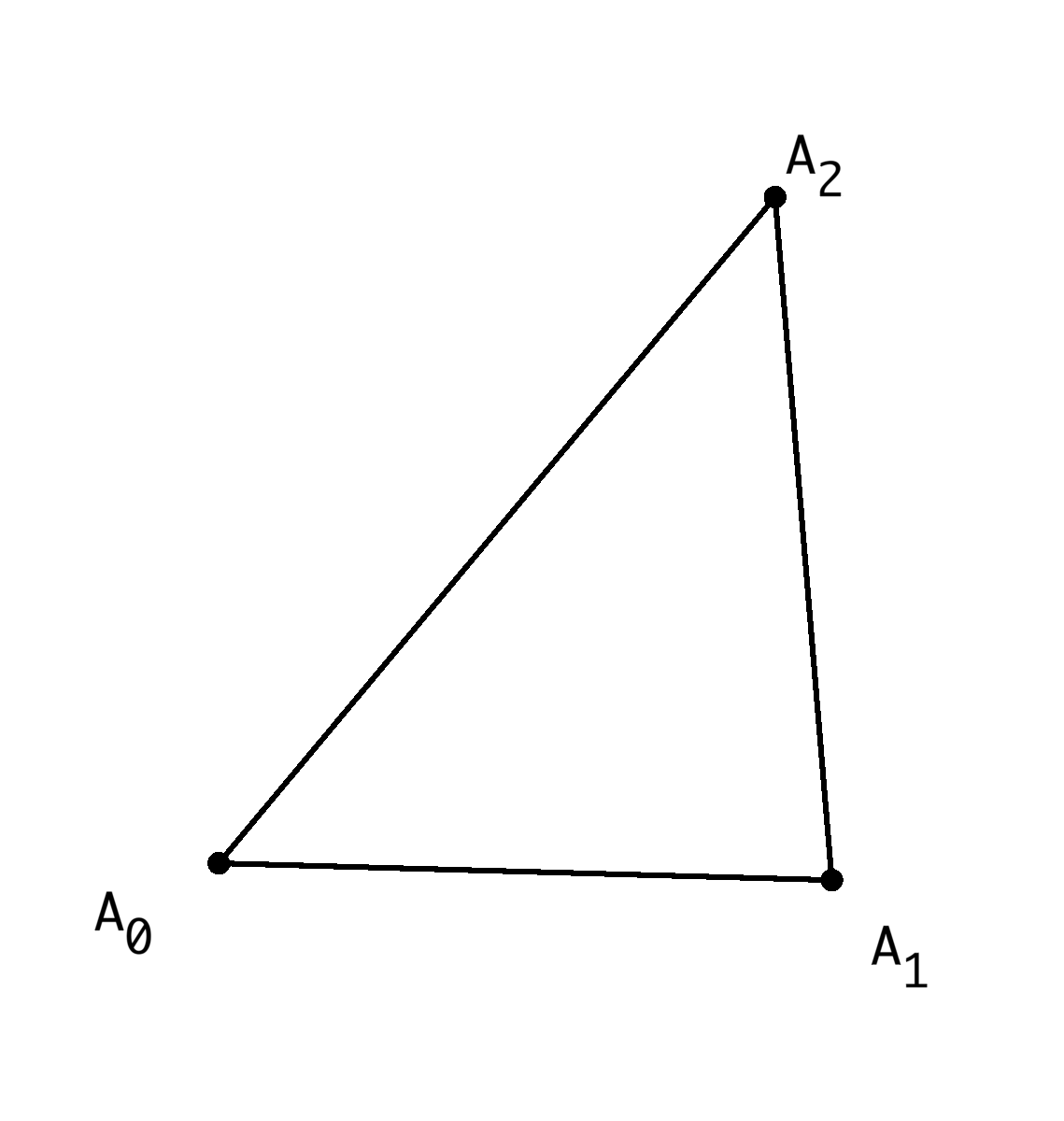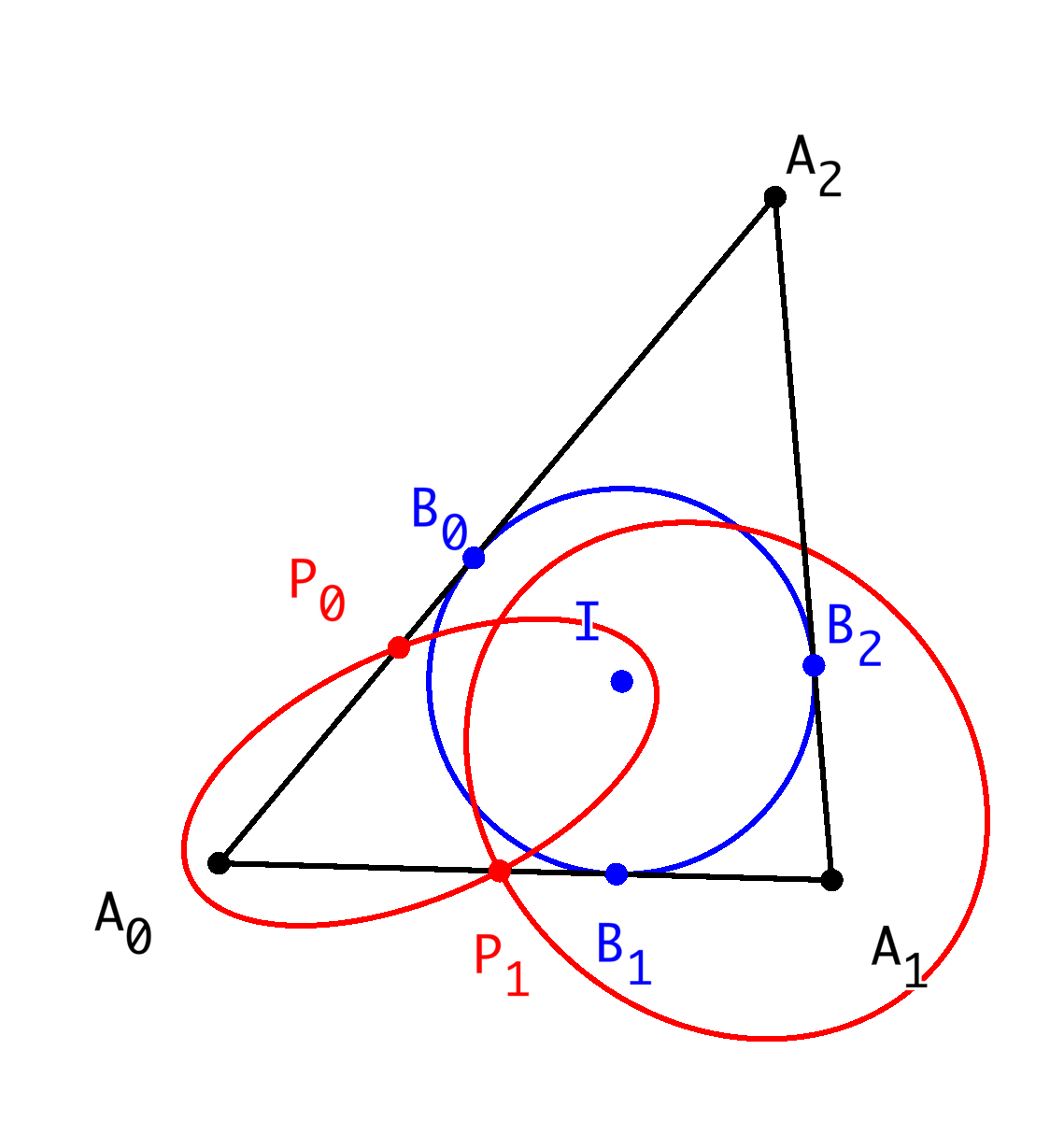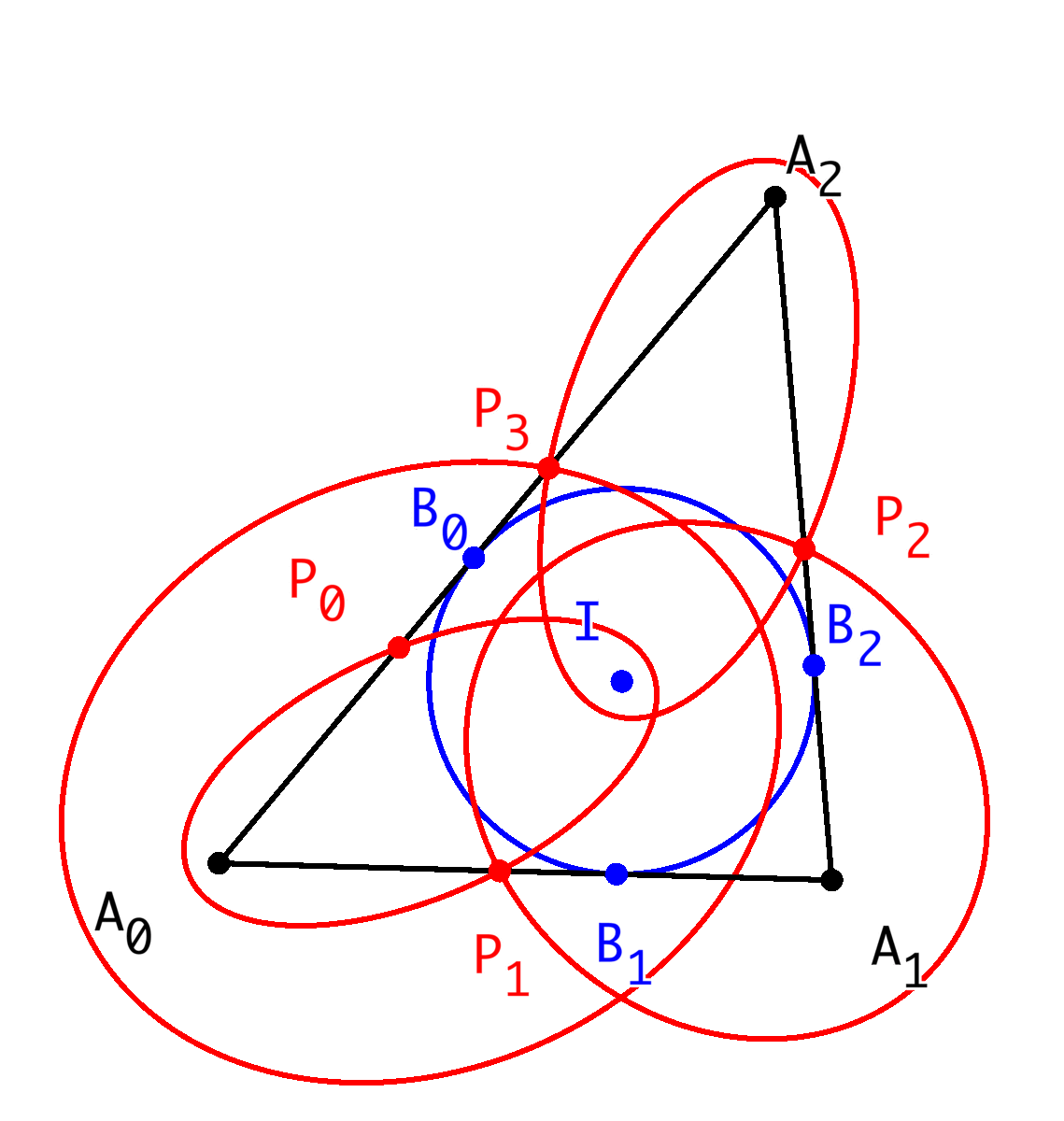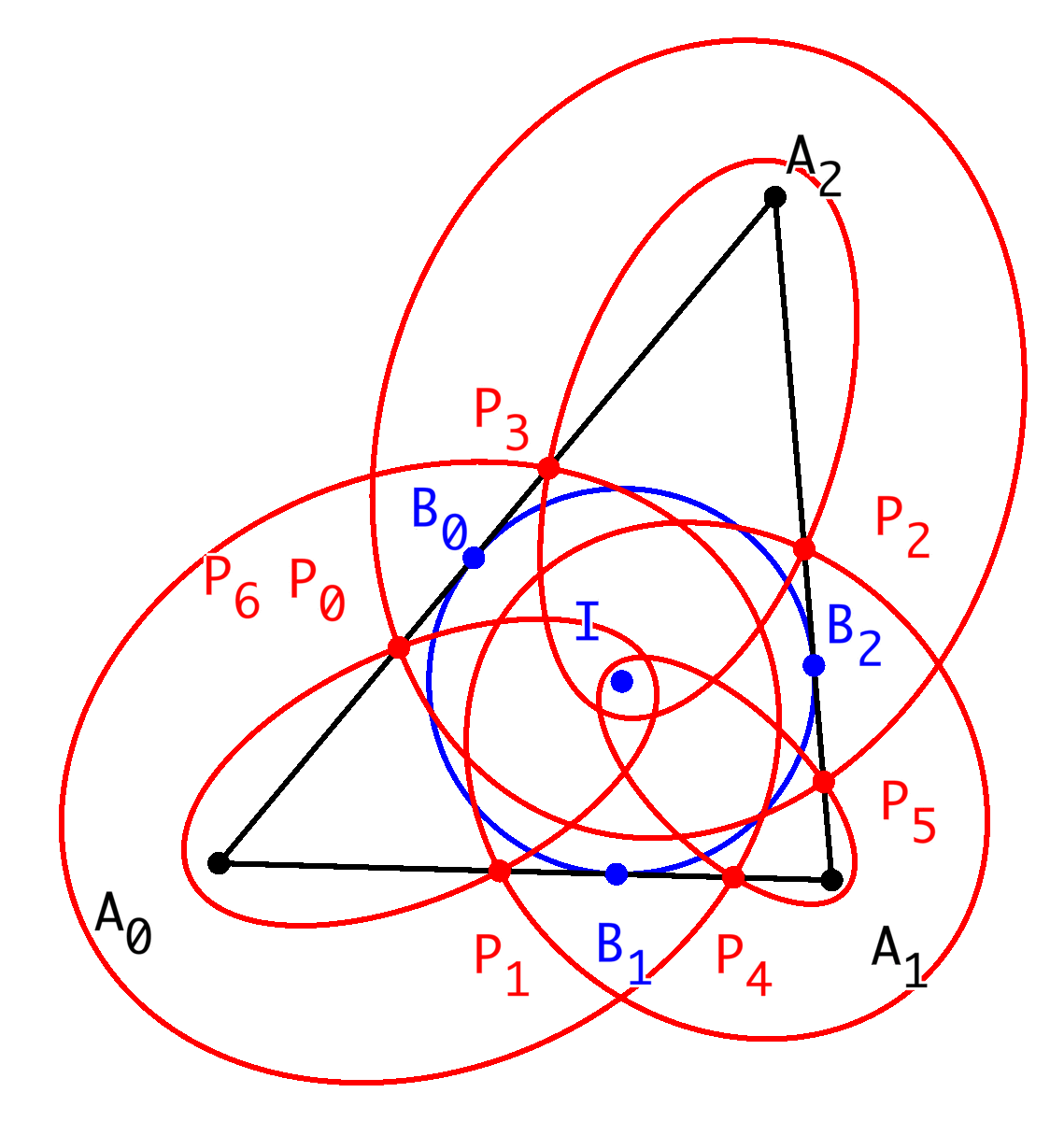
Abb. 2: Schritt für Schritt

2 Beweis der Schließungseigenschaft

Aus Symmetriegründen (Winkelhalbierende als Symmetrieachse) sind die orientierten Abstände B_iP_i und B_i+1P_i+1 (Indizes modulo 3) gleich lang. Daher sind die Abstände B₀P₀ und B₀P₃ entgegengesetzt gleich. Nach einem weiteren Durchgang ist B₀P₀ = B₀P₆ und damit P₀ = P₆.

3 Parität

Beim Dreieck brauchen wir 6 Schritte bis zur Schließung. Allgemein brauchen wir bei einem Tangentenvieleck mit einer ungeraden Eckenzahl 2u Schritte bis zur Schließung. Bei einem Tangentenvieleck mit einer geraden Eckenzahl g brauchen wir lediglich g Schritte.

4 Tangentenviereck

Beim Tangentenviereck hat die Schließungsfigur also die Periodenlänge vier (Abb. 3 und 4).

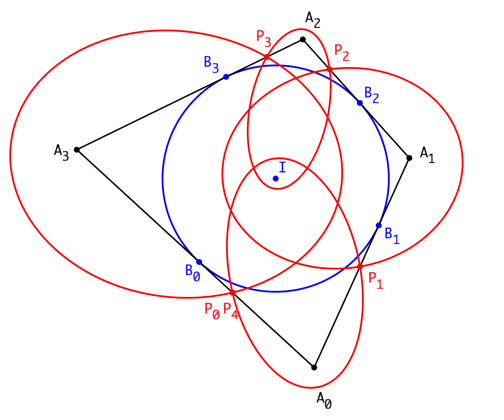
Abb. 3: Tangentenviereck

Abb. 4: Schritt für Schritt

Weblink

Hans Walser: Schließungsfiguren

http://www.walser-h-m.ch/hans/Schliessungsfiguren/index.html