Hans Walser, [20130119a]

Schlinge um Kreis

Anregung: R. S., Z.

1 Die Uralt-Aufgabe

Um einen Kreis mit Radius r wird eine Schlinge im Abstand 1 gelegt (Abb. 1). Wie lang ist die Schlinge im Vergleich zum Kreisumfang?

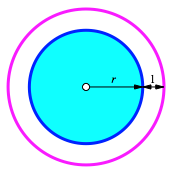
Abb. 1: Schlinge um Kreis im Abstand 1

Rechnung ergibt:

Die Differenz ist vom Kreisradius r unabhängig.

Ursprünglich wurde diese Aufgabe allerdings in der inversen Form serviert: Die Schlinge ist um 1 länger als der Kreisumfang. Wie weit ist sie vom Kreis entfernt?

2 Polygon

Wir machen dasselbe mit einem konvexen Polygon (Abb. 2).

Abb. 2: Abstandskurve um Polygon

Wir zerlegen die Schlinge in gerade Stücke und Kreisbögen (Abb. 3).

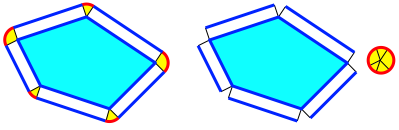
Abb. 3: Zerlegung

Die geraden Stücke haben insgesamt die gleiche Länge wie der Umfang des Polygons. Die Kreisbögen machen insgesamt den Einheitskreis aus. Damit ist , unabhängig von Form und Größe des Polygons.

Den Kreis können wir als Grenzfall eines regelmäßigen n-Ecks mit sehen.

Frage 1: Wie ist das bei nicht-konvexen Polygonen?

Frage 2: Gesucht ein Beispiel mit .

Frage 3: Wie groß ist beim Kreisring (Abb. 4).

Abb. 4: Kreisring

3 Parallelpolygon

Die Schlinge wird gemäß Abbildung 5 ausgelegt. Die Strecken der eckigen Schlinge sind parallel zu den Polygonseiten mit dem Abstand 1.

Frage 4: Haben die Punkte der eckigen Schlinge immer noch den Abstand 1 vom Polygon?

Frage 5: Ist die eckige Schlinge ähnlich zum Polygon?

Abb. 5: Eckige Schlinge

Wie lang ist die eckige Schlinge im Vergleich zum Umfang des Polygons?

Natürlich können wir wieder an den Ecken ausschneiden und die Schnipsel neu zusammenfügen (Abb. 6).

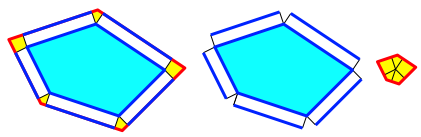
Abb. 6: Ecken einschneiden und neu zusammenfügen

Die Eckenfigur hat einen Inkreis mit dem Radius 1. Der Umfang dieser Eckenfigur, also unser , ist keine Konstante mehr, sondern hängt von den Winkeln des Polygons ab. Immerhin haben wir eine Abschätzung: . Zwei Polygone mit denselben Winkeln haben dasselbe .

Frage 6: Sind Polygone mit denselben Winkeln ähnlich?

Zur Berechnung von benötigen wir also die Winkel des Polygons. Es ist technisch einfacher, mit den Außenwinkeln (für ein Polygon mit n Ecken) zu arbeiten. Mit etwas Trigonometrie ergibt sich:

Frage 7: Wie lautete diese Formel für ein regelmäßiges n-Eck? Was geschieht bei ?

4 Rund um die Erde

Frage 8: Hat Magellan wirklich die Erde umrundet?

Die Schlingenaufgabe wird oft im Zusammenhang mit der Erdkugel formuliert: Wie viel länger als der Erdumfang ist die Schlinge im Abstand 1m von der Erde? Dabei wird stillschweigend vorausgesetzt, dass die Schlinge als Abstandskurve von einem Großkreis der Erdkugel genommen wird, zum Beispiel vom Äquator. In diesem Fall ist natürlich .

Frage 9: Wie ist es, wenn die Schlinge 1m senkrecht oberhalb eines Breitenkreises um die Erde gelegt wird? Vorstellung: Auf Pfählen in der Höhe 1m. In der Abbildung 7 ist die Situation für die geografische Breite dargestellt, allerdings ist die Erdkugel viel zu klein gezeichnet. Eher der Planet des Petit Prince.

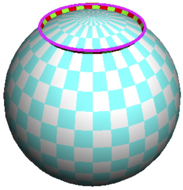
Abb. 7: Schlinge um die Kugel auf 60° Nord und 1m Höhe

Frage 10: Wie ist es, wenn die Schlinge 1m südlich des Breitenkreises auf der Erdoberfläche um die Erde gelegt wird? In der Abbildung 8 ist die Situation für die geografische Breite dargestellt, allerdings ist die Erdkugel viel zu klein gezeichnet.

Abb. 8: Schlinge 1m südlich des Breitenkreises 60° Nord

5 Andere Dimensionen

Wir ersetzen die Schlinge um die Kugel durch einen Sack (im Abstand 1) um die Kugel. In der Abbildung 9 ist der halbe Sack gezeichnet.

Abb. 9: Die Kugel im Sack

Wie groß ist die Flächendifferenz zwischen der ganzen Sackfläche und der Kugeloberfläche? Wir erhalten:

hängt linear von r ab.

Frage 11: Wie ist es in der nächsten Dimension?

6 Bearbeitung der Fragen

Bearbeitung der Frage 1: Bei nicht-konvexen Polygonen gibt es keine Konstante für .

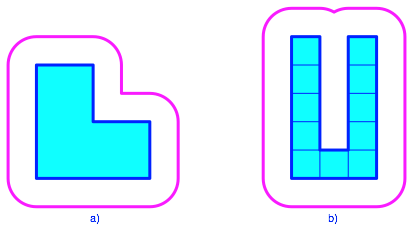
Abb. 10: Nicht-konvexe Beispiele

Im Beispiel der Abbildung 10a) ist .

Im Beispiel der Abbildung 10b) ist .

Bearbeitung der Frage 2: Es gibt viele Lösungen. Die Abbildung 11 zeigt ein Beispiel. In diesem Beispiel ist .

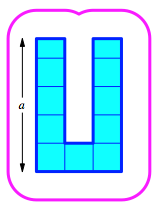
Abb. 11: Schlingenlänge = Umfang

Bearbeitung der Frage 3: Es sei R der Außenradius und r der Innenradius (Lochradius) des Kreisringes. Fallunterscheidung bezüglich r:

(I) : In diesem Fall ist .

(II) : Wir erhalten . Dies ist abhängig von r.

Bemerkung: Die „hässlichen“ Fälle der Abbildungen 10b) und 11 können umgangen werden, wenn wir den kanonischen Abstand 1 durch den Abstand ersetzen und dann den Grenzwert

bestimmen. Für den Fall des Kreises ergibt sich , also soweit nichts neues.

Allgemein kommen wir so zum Konzept der integralen Krümmung.

Bearbeitung der Frage 4: Im Bereich der Ecken ist der Abstand vom Polygon größer als 1.

Bearbeitung der Frage 5: Das eckige Schlingenpolygon ist genau dann ähnlich zum Ausgangspolygon, wenn dieses einen Inkreis hat. Im Beispiel der Abbildung 5 ist dies nicht der Fall.

Bearbeitung der Frage 6: Nein. Gegenbeispiel: Zwei Rechtecke mit ungleichen Seitenverhältnissen. Lediglich bei Dreiecken kann aus der Gleichheit der Winkel die Ähnlichkeit gefolgert werden.

Bearbeitung der Frage 7: Für ein regelmäßiges n-Eck ergibt sich:

Für erhalten wir geometrisch einen Kreis. Rechnerisch können wir die Sau herauslassen: mit der Regel von Bernoulli-de l’Hôpital ergibt sich:

Nun ja, das wissen wir schon lange.

Bearbeitung der Frage 8: Magellan selber starb während der Reise auf den Philippinen. Lediglich 18 Männer der ursprünglichen 237 Männer kehrten mit einem von ursprünglich 5 Schiffen in den spanischen Ausgangshafen zurück. Dabei wurden etwa 69'000 km zurückgelegt (für den Seemann im Ausguck einige Meter mehr), jedenfalls weit mehr als der Erdumfang. Die Erdumrundung geschah jedoch nicht auf einem Großkreis, was schon aus topografischen Gründen nicht möglich gewesen wäre.

Die sophistische Frage ist, ob etwa eine Rundreise streng auf einem Breitenkreis als Erdumrundung zählen kann. Man geht zwar um die Erdachse herum, aber der zurückgelegte Weg ist kürzer als der Erdumfang. Ein kleiner Spaziergang um den Nordpol ist wohl noch keine Erdumrundung.

Bearbeitung der Frage 9: Es sei r der Erdkugelradius. Damit wird:

hängt von der geografischen Breite ab.

Bearbeitung der Frage 10: Wir erwarten nach Bearbeitung der Frage 9 natürlich in diesem Fall . Das ist, cum grano salis, richtig. Exakt gilt:

Um die Situation für die Erdkugel mit zu klären, machen wir den Grenzübergang . Es sind die beiden r-haltigen Terme und zu untersuchen. Mit Bernoulli-de l’Hôpital ergibt sich:

und

Somit ist:

Für gilt daher .

Bearbeitung der Frage 11: Wir behandeln die Sache gleich allgemein. Im hat die eingebettete Sphäre die Oberfläche:

Somit ist:

Das ist eine Polynomfunktion in r vom Grad . Genau im Fall des Kreises der Uraltaufgabe ergibt sich eine von Null verschiedene Konstante.